(a) Derive an expression for the energy stored in a parallel plate capacitor of capacitance C when charged up to voltage V. How is this energy stored in the capacitor ?
(b) A capacitor of capacitance 1 μF is charged by connecting a battery of negligible internal resistance and emf 10 V across it. Calculate the amount of charge supplied by the battery in charging the capacitor fully.
Text Solution
The correct Answer is:a
(a) Let at a particular instant charge on the plate of capacitor be q and its potential difference be qC. If an additional charge dq is given to the capacitor plate, work done for it is given by
dW=(qC).dq
Therefore, whole process of charging from Oto Q requires a work
W=∫Q0qdqC=1C[q22]Q0=Q22C
This work done is stored as the electrostatic potential energy of the charged capacitor. Hence, potential energy of charged capacitor
u=Q22C
But Q = CV, where V be the potential difference between the plates of capacitor, hence
u=Q22C=12QV=12CV2
This energy is stored within the dielectric of the capacitor in the form of electrostatic potential energy.
(b) Here capacitance C =1μF=1×10−6F emf of battery E = 10 V and internal resistance of battery r= 0.
Since r = 0, hence potential difference between the plates of capacitor, when it is fully charged is V = ε = 10 V.
∴ Charge supplied by the battery to the capacitor Q =CV=(1×10−6F)×10V
=10×10−6C=10μC
|
Topper's Solved these Questions
- EXAMINATION PAPER 2020 (SOLVED)BOOK - U-LIKE SERIESCHAPTER - EXAMINATION PAPER 2020 (SOLVED)EXERCISE - SECTION C
8 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - U-LIKE SERIESCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SELF ASSESSMENT TEST
1 Videos
- MAGNETISM AND MATTERBOOK - U-LIKE SERIESCHAPTER - MAGNETISM AND MATTEREXERCISE - SELF ASSESSMENT TEST (Section D)
1 Videos
Similar Questions
Knowledge Check
A capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4JA capacitor of capacitance 700 pF is charged by 100 V battery. The electrostatic energy stored by the capacitor is
A2.5×10−8JB3.5×10−6JC2.5×10−4JD3.5×10−4JA capacitor of capacitance 100(μ)F is charged by connecting it to a battery of emf 12 V and internal resistance 2(Ω). (a) Find the time constant of the circuit. (b) Find the time taken before 99% of maximum charge is stored on the capacitor.
A0.92msB0.4msC0.8msD0.1ms
Parallel Plate Capacitor |Energy Stored In A Charged Capacitor
View SolutionA parallel plate capacitor of capacitance C0 is connected across a battery of voltage V. Calculate the change in energy stored in the capacitor if distance between both the plates is decreased to half of its original value.
View SolutionA capacitor of capacitance 13μF is connected to a battery of 300volt and charged. Then the energy stored in capacitor is
View SolutionA capacitor of capacitance 10μF is charged by connecting through a resistance of 20Omga and battery of 20 V. What is the energy supplied by the battery?
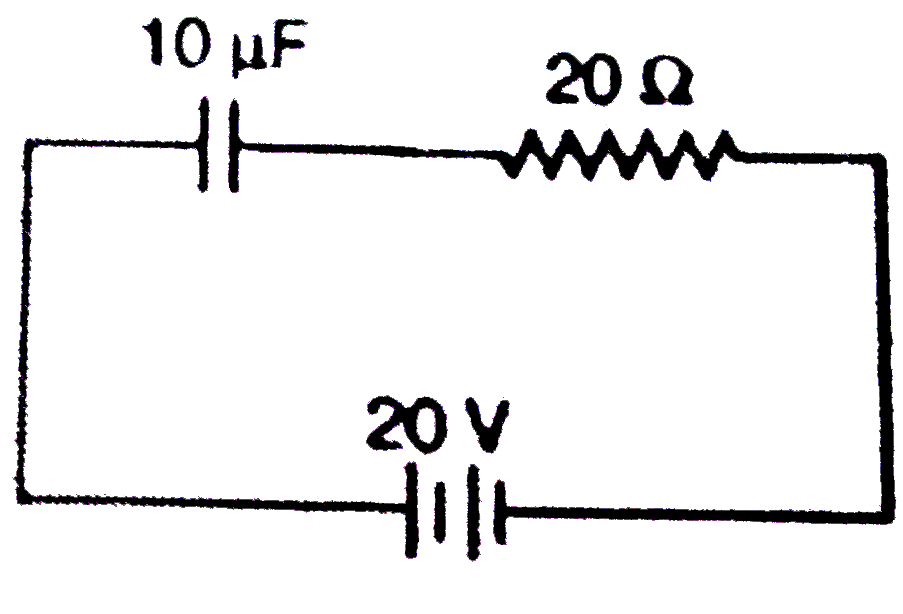
View SolutionA capacitor of capacity 10μF is subjected to charge by a battery of 10 V. Calculate the energy stored in the capacitor.
View Solution
