A disc is rotating with constant angular velocity ω in anticlockwise direction. An insect sitting at the centre (which is origin of our co-ordinate system) begins to crawl along a radius at time t=0 with a constant speed V relative to the disc. At time t=0 the velocity of the insect is along the X direction.
(a) Write the position vector (→r) of the insect at time ‘t’.
(b) Write the velocity vector (→v) of the insect at time ‘t’.
(c) Show that the X component of the velocity of the insect become zero when the disc has rotated through an angle θ given by tanθ=1θ.
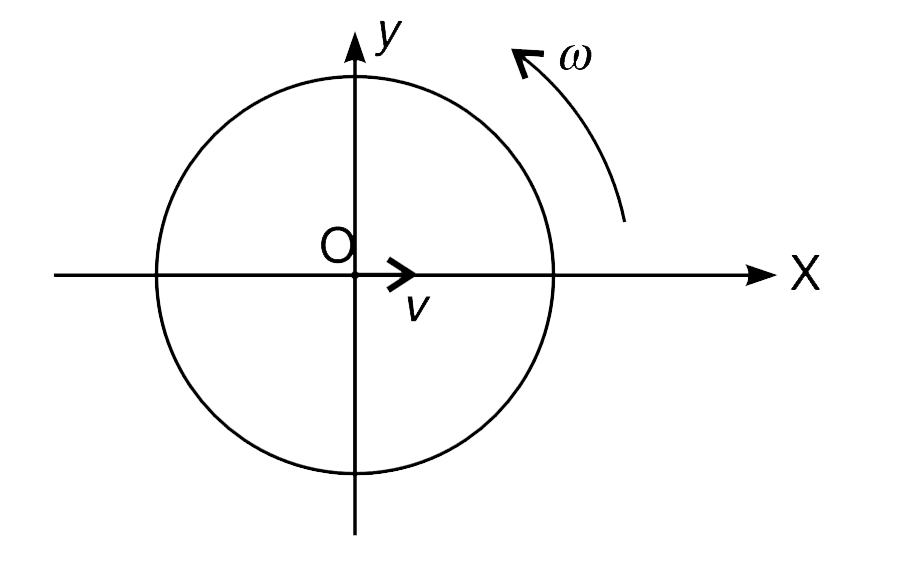
The correct Answer is:(a) →r=vt[cos(ωt)ˆi+sin(ωt)]ˆj
(b) →Vp=V[cos(ωt)−ωtsin(ωt)]
ˆi+V[sin(ωt)+ωtcos(ωt)]ˆj
Step by step video, text & image solution for A disc is rotating with constant angular velocity omega in anticlockwise direction. An insect sitting at the centre (which is origin of our co-ordinate system) begins to crawl along a radius at time t = 0 with a constant speed V relative to the disc. At time t = 0 the velocity of the insect is along the X direction. (a) Write the position vector (vec(r)) of the insect at time ‘t’. (b) Write the velocity vector (vec(v)) of the insect at time ‘t’. (c) Show that the X component of the velocity of the insect become zero when the disc has rotated through an angle theta given by tan theta = (1)/(theta). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 2
58 Videos
- KINEMATICSBOOK - ARIHANTCHAPTER - KINEMATICSEXERCISE - Level 3
33 Videos
- HEAT TRANSFERBOOK - ARIHANTCHAPTER - HEAT TRANSFEREXERCISE - Heat Transfer
45 Videos
- KINETIC THEORY OF GASESBOOK - ARIHANTCHAPTER - KINETIC THEORY OF GASESEXERCISE - Level 3
4 Videos
Similar Questions
Two friends A and B are running on a circular track of perimeter equal to 40 m. At time t=0 they are at same location running in the same direction. A is running slowly at a uniform speed of 4.5km/hr whereas B is running swiftly at a speed of 18km/hr.
(a) At what time t0 the two friends will meet again?
(b) What is average velocity of A and B for the interval t=0 to t=t0?
View SolutionA car manufacturer usually tells a optimum speed (V0) at which the car should be driven to get maximum mileage. In order to find the optimum speed for a new model, an engineer of the car company experimented a lot and finally plotted a graph between the extreme time t (defined as number of hours a tank full of petrol lasts) vs the constant speed V at which car was run.
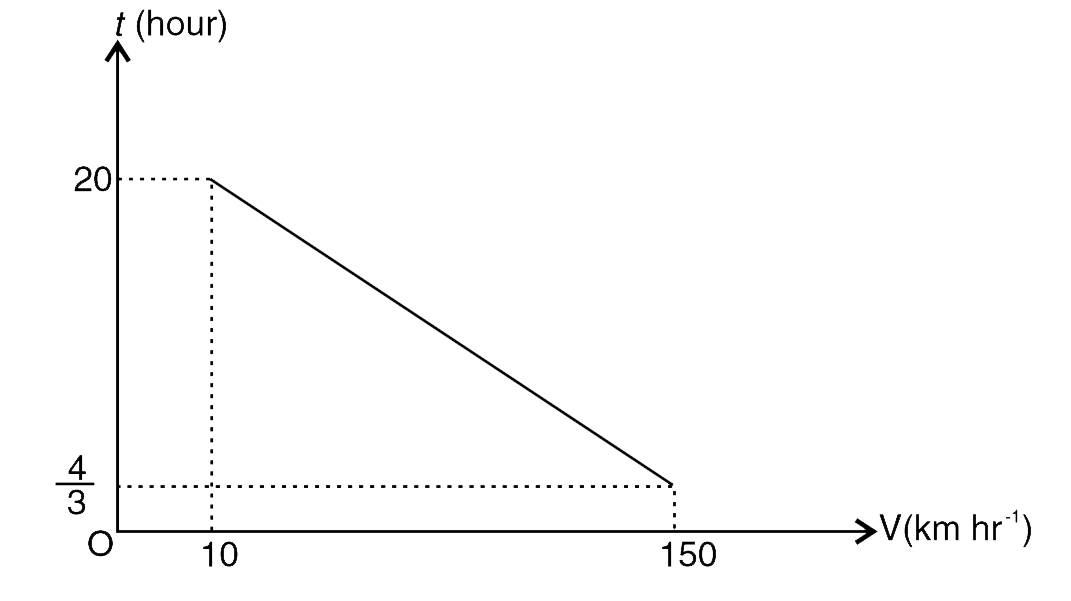
(a) Calculate the optimum speed V0 for this new model.
(b) If the fuel tank capacity of this car is 50 litre, what maximum mileage can be obtained from this car?
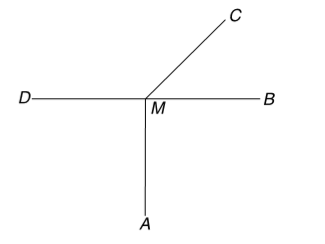
View SolutionFour metal rods each of length L and cross sectional area A are joined at point M. Thermal conductivities of MA, MB and MD are equal and that of MC is thrice that of MA. The end points A, B, C and D are kept in large reservoirs. Heat folws into the junction from B at a rate of P(Js−1) and C from at a rate of 3P. Heat flows out of D at a rate of 5P.
(a) Find the relation between temperatures of points A, B and C.
(b) Find temperature of D if temperature of A and M and TA and TM respectively.
View SolutionAn ideal gas is inside a cylinder with a piston that can move freely. The walls of the cylinder and piston are non- conducting. The piston is being moved out of the cyl- inder at a constant speed u.
(a) Consider a gas molecule of mass m moving with speed v(>>u). It hits the piston elastically at an angle of incidence q. Calculate the loss in kinetic energy of the molecule.
(b) If the area of piston is A and pressure of the gas is P, calculate the rate of decreases of molecular kinetic energy of the gas sample.
(c) Ifu>> molecular velocities, at what rate will the gas lose its molecular kinetic energy

View SolutionA rotating disc moves in the positive direction of x-axis as shown. Find the equation y(x) describing the position of the instantaneous axis of rotation if at the initial moment the centre C of the disc was located at origin after which
a. it moved with constant acceleration a (initial velocity zero) while the disc rotating anticlockwise with constant angular velocity ω. b. it moved with constant velocity v while the disc started rotating anticlockwise with a constant angular acceleration a (with initial angular velocity zero).

View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0. Find the velocity vector and position vector of the particle vec v (t) and vec r (t) in relation with time.
View SolutionA horizontal disc rotates with a constant angular velocity omega=6.0rad//s about a vertical axis passing through its centre. A diameter of the disc with a velocity v^'=50cm//s which is constant relative to the disc. Find the force that the disc exerts on the body at the moment when it is located at the distance r=30cm from the rotation axis.
View SolutionIn the previous problem, initially the insect is at the edge and the disc is rotating with angular speed ω0 in clockwise direction. Now the insect starts walking along the rim with speed v relative to the disc also in clockwise direction. Find new angular speed of platfrom.
View SolutionA cockroach is moving with velocity v in anticlockwise direction on the rim of a disc of radius R of mass m. The moment of inertia of the disc about the axis is I and it is rotating in clockwise direction with an angular velocity ω. If the cockroach stops, the angular velocity of the disc will be
View SolutionAn electron is at P t = 0 It is circulating in anticlockwise direction with a constant angular speed omega along the shown circular path. Magnetic field at Q(CQ = 2R , where R is radius of the circular) will be recorded as zero at times)
View SolutionA horizontal disc of radius R and mas 20 M is pivoted to rotate freely about a vertical axis through its centre. A small insect A of mass M and another small insect B of mass mM4 are initially at diametrically opposite points on the periphery of the disc. The whole system is imparted an angular speed ω0 Insect A walks along the diameter with constant velocity v relative to the disc unit it reaches B which remains at rest on the disc. A then eats B and returns to its starting point along the original path with same speed v relative to the disc.
(a) Find the angular speed of the disc when A reaches the centre after eating B.
(b) Plot approximately, the variation of angular speed of the disc with time for the entire journey of the insect A.
View SolutionA insect of mass m stands on a horizontal disc platform of moment of inertia 1 which is at rest. What is the angular velocity of the disc platform when the insect goes along a circle of radius r, concentric with the disc, with velocity v relative to the disc.
View SolutionA disc of radius R start at time t=0 moving along the positive X-axis with linear speed b and angular speed omega . Find the x and y-coordinates of the bottommost point at any time t.
View SolutionAn ant travels along a long rod with a constant velocity ii relative to the rod starting from the origin. The rod is kept initially along the positive x-axis. At t = 0, the rod also starts rotating with an angular velocity w (anticlockwise) in x-y plane about origin. Then
View SolutionA force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity omega in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
View Solution
