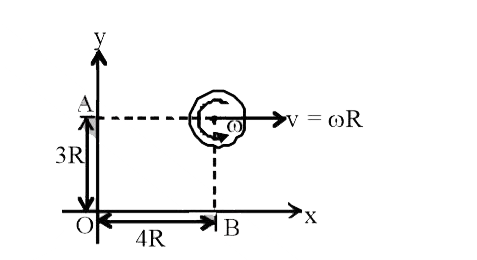
A disc of mass M and radius R is rolling with angular speed $ω$ on a horizontal plane as shown in fig. The magnitude of angular momentum of the disc about the origin is :

$\frac{1}{2} M R^{2} ω$

$M R^{2} ω$

$2 M R^{2} ω$

$\frac{3}{2} M R^{2} ω$

Text Solution

Verified by Experts

The correct Answer is:D

A disc of mass M and radius R is rolling with angular speed $ω$ on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A $(1 / 2) M R^{2} ω$
B $M R^{2} ω$
C $(3 / 2) M R^{2} ω$
D $2 M R^{2} ω$
A disc of mass $m$ and radius $R$ moves in the $x - y$ plane as shown in Fig. The angular momentum of the disc about the origin $O$ at the instant shown is

A $- \frac{5}{2} m R^{2} ω ˆ k$
B $\frac{7}{3} m R^{2} ω ˆ k$
C $- \frac{9}{2} m R^{2} ω ˆ k$
D $\frac{5}{2} m R^{2} ω ˆ k$