
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.

As we have discussed, angular momentum about O is the vector sum of two terms:
Iω and mvr⊥
Here, Iω=Icmω=(12mR2)(vR)=12mvR (perpendicular to paper inwards)
and mvr⊥=mvcr⊥=mRv (perpendicular to paper inwards)
Since, both the terms are in the same direction
Ltotal=12mvR+mvR
or Ltotal=32mvR (perpendicular to paper inwards)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A solid sphere is set into motion on a rough horizontal surfce with a linar speed v in the forward direction and an angular speed v/R in the anticlockwise direction as shown infigure . Find the linear speed of the sphere a. where it stops rotating and b. when slipping finally ceases sand pure rolling starts.

View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:

View Solution
Knowledge Check
A solid sphere is set into motion on a rough horizontal surface with a linear velocity v in the forward direction and an angular velocity v/R in the anticlockwise direction as shown in the figure. Find the linear speed of the sphere, when it stops rotating.
 Av5Bv7C3v5D3v7
Av5Bv7C3v5D3v7A disc of mass M and radius R is rolling with angular speed ω on a horizontal plane. The magnitude of angular momentum of the disc about a point on ground along the line of motion of disc is :
A(1/2)MR2ωBMR2ωC(3/2)MR2ωD2MR2ωFind the ratio of magnitude of angular momentu of a rolling disc about origin to that about the point P on the disc, as shown in the figure.
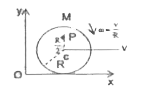 A2:1B1:1C1:3D4:3
A2:1B1:1C1:3D4:3
A disc of mass M and radius R is rolling with angular speed w on horizontal plane as shown. The magnitude of angular momentum of the disc about the origin O is :

View SolutionA solid sphere of radius R is set into motion on a rough horizontal surface with a linear speed v0 in forward direction and an angular with a linear speed v0 in forward direction and an angular velocity ω0=v0/2R in counter clockwise direction as shown in figure. If coefficient of friction μ then find
a. the time after which sphere starts pure rolling,
b. the linear speed of sphere when it starts rolling and
c. the work down by friction over a long time.
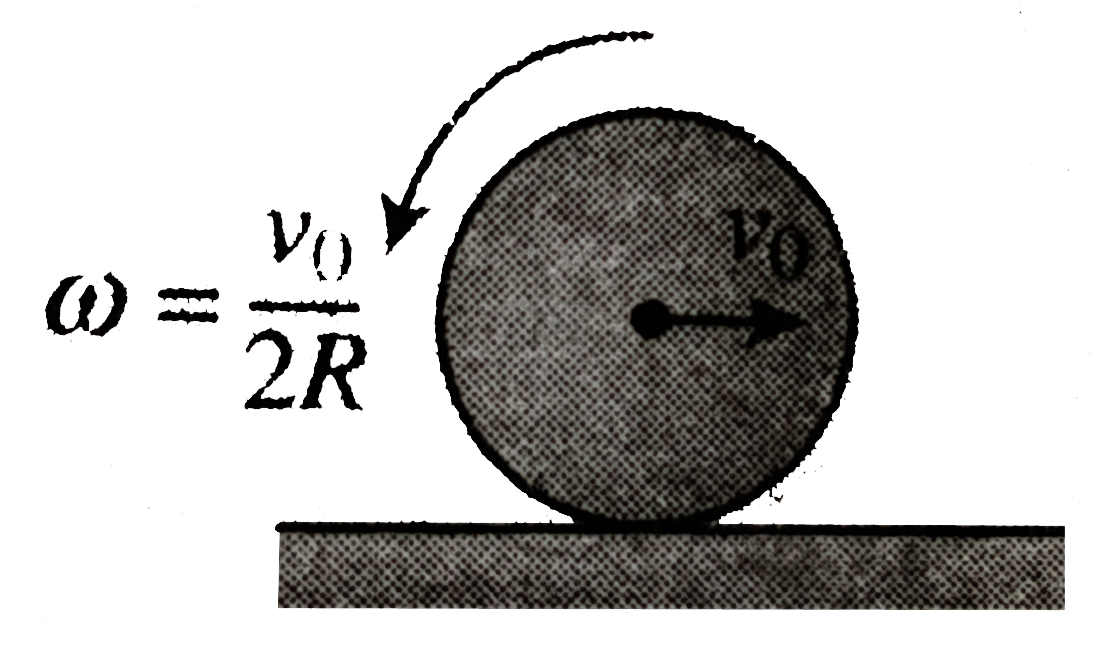
View SolutionFind the angular momentum of a disc about the axis shown in figure in the following situations.

View SolutionA uniform circular disc of mass m is set rolling on a smooth horizontal table with a uniform linear velocity v. Find the total K.E. of the disc.
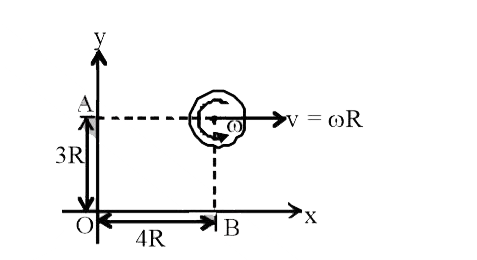
View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
View Solution
