A disc of metal of raidus r with its plane vetical can be made to swing about a horiziontal axis passsing through any one of a series of holes bored along a diameter. Show that the minimum period of oscillatin is given by t=2π√1.414rg
Step by step video & image solution for A disc of metal of raidus r with its plane vetical can be made to swing about a horiziontal axis passsing through any one of a series of holes bored along a diameter. Show that the minimum period of oscillatin is given by t=2pi sqrt(1.414r)/(g) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - NN GHOSHCHAPTER - SIMPLE AND COMPOUND PENDULUMEXERCISE - Exercise24videos
SIMPLE AND COMPOUND PENDULUM
- BOOK - NN GHOSHCHAPTER - SECOND LAW OF THERMODYNAMICSEXERCISE - All Questions7videos
SECOND LAW OF THERMODYNAMICS
- BOOK - NN GHOSHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Eexercies39videos
SIMPLE HARMONIC MOTION
Similar Questions
A rigid mass less rod of length L is rotating in a vertical plane about a horizontal axis passing through one of its ends. At the other end of the rod there is a mass less metal plate welded to the rod. This plate supports a heavy small bead that can slide on the rod without friction. Just above the bead there is another identical metal plate welded to the rod. The bead remains confined between the plates. The gap between the plates is negligible compared to L. The angular speed of the rod when the bead is at lowest position of the circle is ω=2√gL. How many times a clink of the bead hitting a metal plate is heard during one full rotation of the rod ?
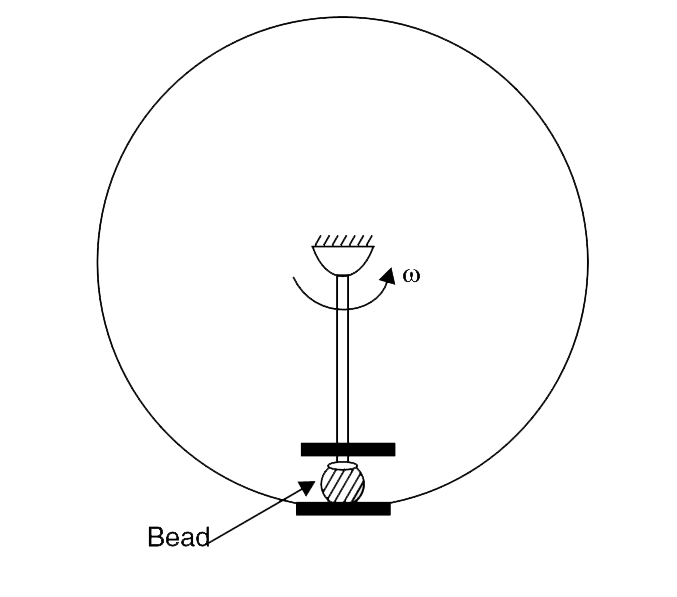 View Solution
View SolutionA uniform circular disc of mass m and radius a,can rotate in a vertical plane about a horizontal axis through a point O on its circumference.The disc is held with the diameter OA through O horizontal and then released. If a constant frictional couple of mga2π opposes the motion, the angular speed when OA is vertical will be
1) √g2a
2) √ga
3) √g3a
4) √2g3aView Solution
Knowledge Check
- Question 1 - Select One
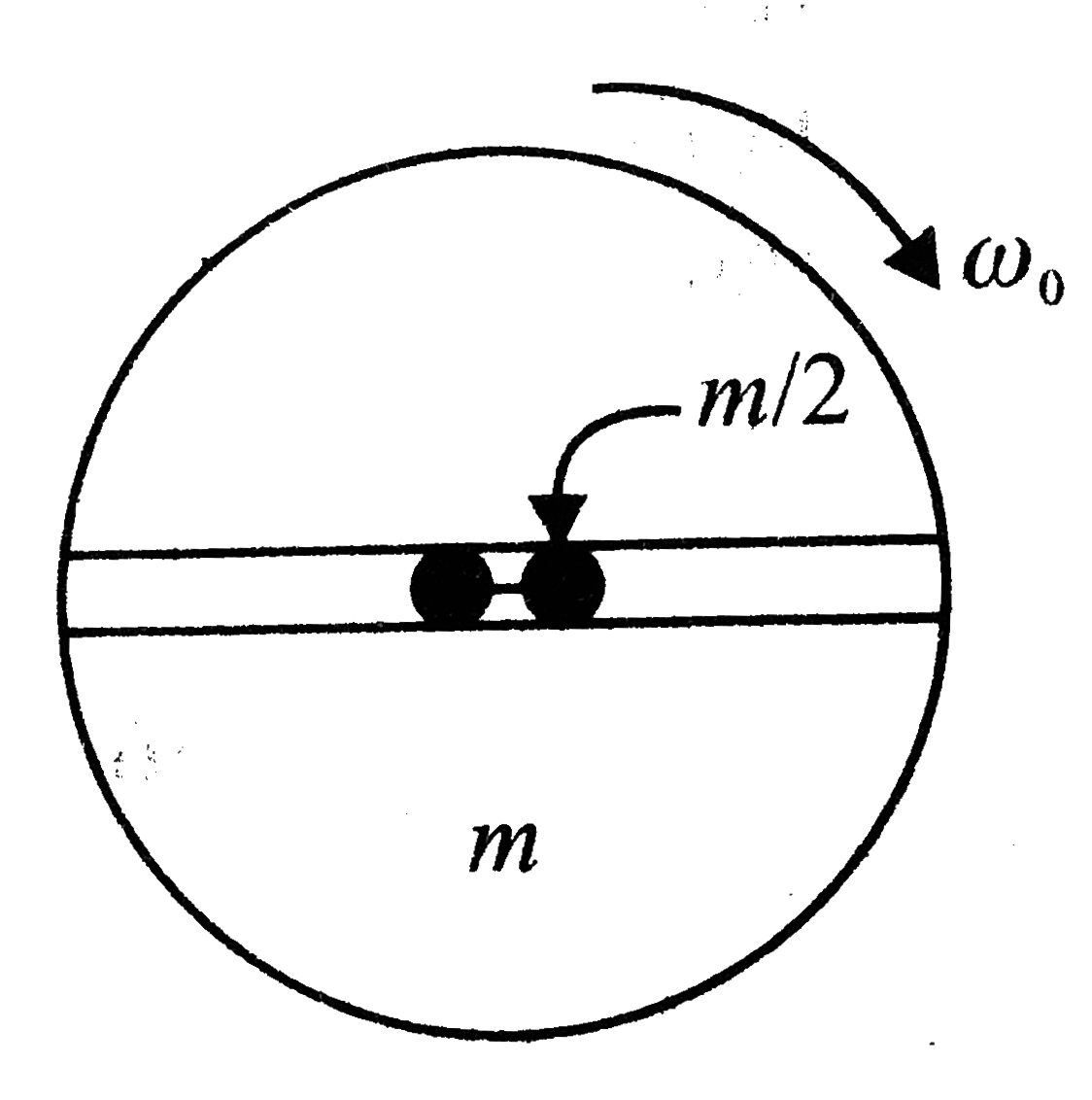
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The net work done by forces exerted by the disc on the ball for the duration ball remains on the disc isA2mR2ω209BmR2ω2018CmR2ω206DmR2ω209 - Question 2 - Select One
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.

The angular speed of the disc when the balls reach the end of the disc isAω02Bω03C2ω03Dω04 - Question 3 - Select One
A disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity ω0 and released.
The speed of each ball relative to the ground just after they leave the disc is
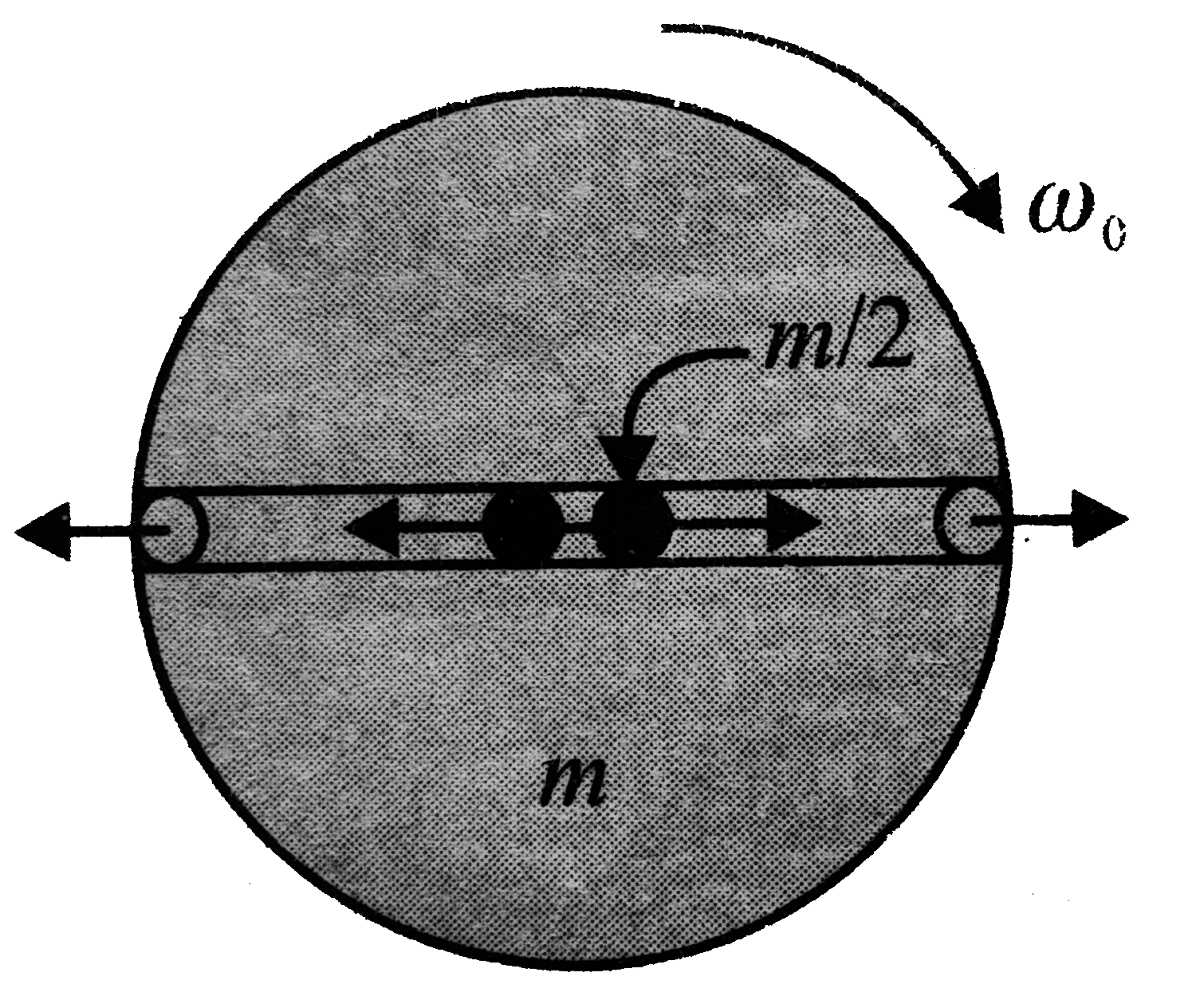 ARω0√3BRω0√2C2Rω03Dnone of these
ARω0√3BRω0√2C2Rω03Dnone of these
An annular ring of internal and outer radii r and R respectively oscillates in a vertical plane about a horizontal axis perpendicular to its plane and passing through a point on its outer edge. Calculate its time period and show that the length of an equivalent simple pendulum is 3R2 as r→0 and 2R as r→R.
View SolutionA disc of mass 4kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass 2kgeachareplaced∈itoneithersofthecentreofthediscasshown∈figure.Thediscisgiven∈itialanga––rvelocityomega_(0)=12 (rad) / (s) released. Find the angular speed of disc (in radian/s) when the balls reach the ends to disc.
'(##CEN_KSR_PHY_JEE_C09_E01_016_Q06##)'View SolutionTwo identical uniform thin rods have been connected at right angles to form a ‘T’ shape. One end of a rod is connected to the centre of the other rod. Length of each rod is L. The upside down ‘T’ can swing like a pendulum about a horizontal axis passing through the top end (see fig.). Axis is perpendicular to plane of the fig. The speed of the meeting point of the two rods is u=2√gL when it is at its lowest position. Calculate the angular acceleration of the ‘T’ shaped object when it is at extreme position of its oscillation.
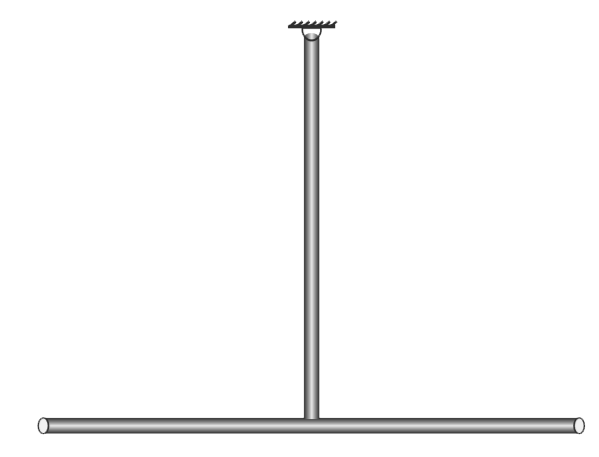 View Solution
View SolutionIn the figure shwon there is non-conducting disc of mass M=2k and radius R=4m. On its upper & lower part of circumference +Q and −Q charge are uniformly attached such that liner charge density is QπR. The disc can freely rotate about an horizontal axis passing through O. There is a uniform electric field ¯¯¯E in the vertical direction such that QE=mg. If the disc is rotated by a small angle it performs S.H.M. its time period is given by T=≈√πn then, P+n, is (Take π2=g)
 View Solution
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity ω0 =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
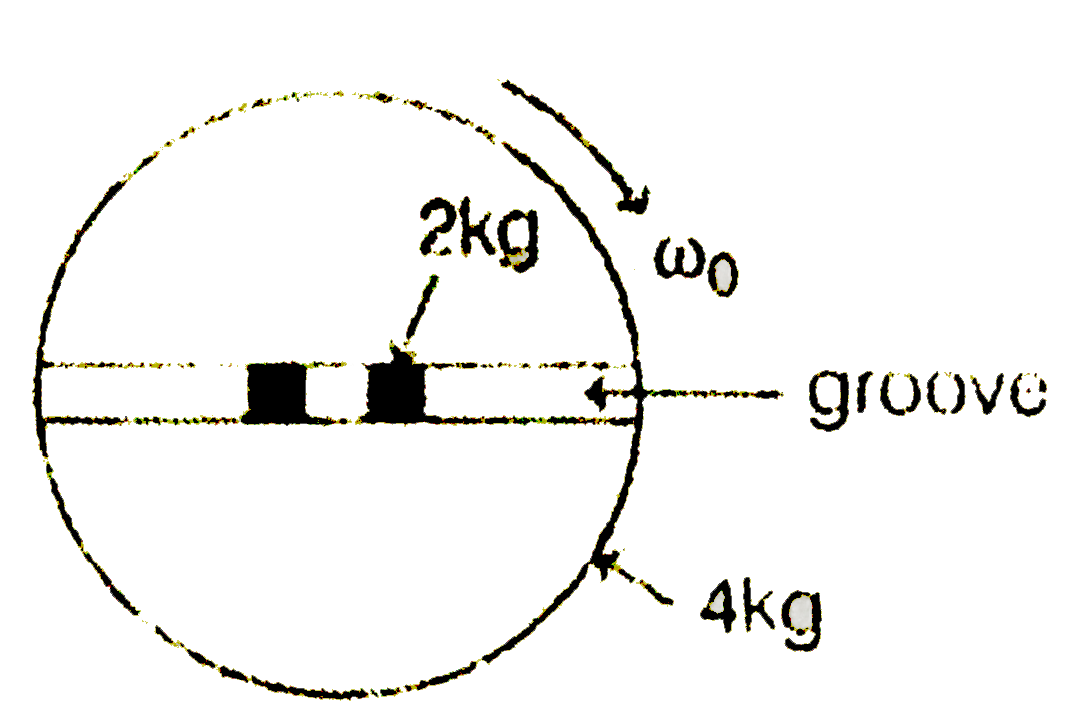 View Solution
View Solution

