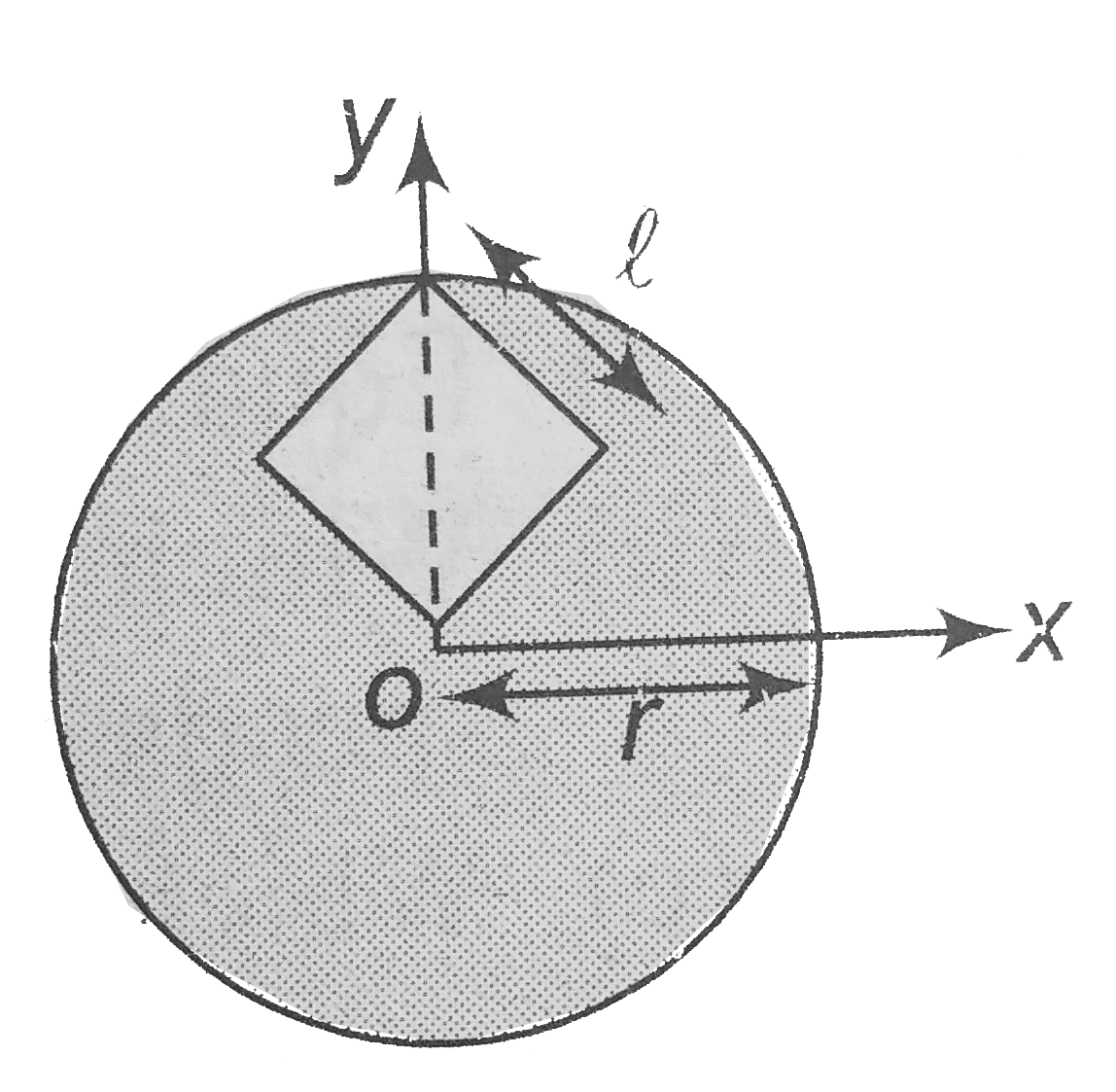
A disc (of radius r cm) of uniform thickness and uniform density σ has a square hole with sides of length l=r√2cm. One corner of the hole is located at the centre of the disc and centre of the hole lies y-axis as shown. Then the y-coordinate of position of centre of mass of disc with hole (in cm) is.
 .
.
−r2(π−1/4)
−r4(π−1/4)
−r4(π−1/2)
−3r4(π−1/4)
The correct Answer is:C
( c) This disc can be assumed to be made of a complete uniform disc and a square plate with same negative mass density.
Ycm=m1y1+m2y2m1+m2=(πr2)σ(0)+l2(−σ)(r/2)πr2σ+l2(−σ)
=−l2r2(πr2−l2)=−r222(πr2−r22)=−r4(π−12).
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Displacement , Velocity And Acceleration Of Centre Of Mass
30 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia
39 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
Similar Questions
Knowledge Check
From a uniform disc of radius R, an equilibatered triangle of side √3R is cut as shown. The new position of centre of mass is:
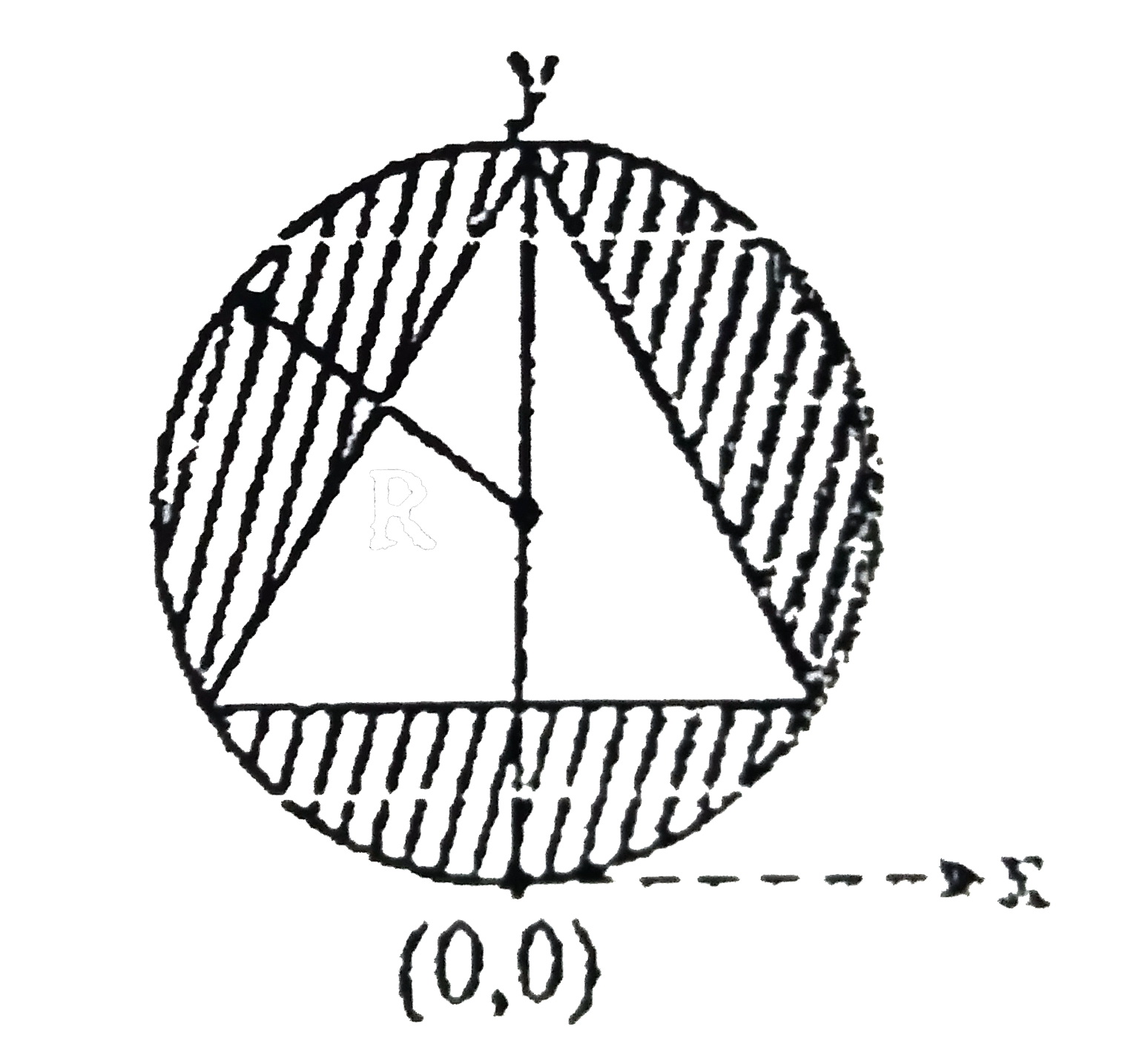 A(0,0)B(0,R)C(0,√3R2)Dnone of these
A(0,0)B(0,R)C(0,√3R2)Dnone of theseFrom a uniform disc of radius R, an equilateral triangle of side √3R is cut as shown in the figure. The new position of centre of mass is :
 A(0,0)B(0,R)C(0,√3R2)Dnone of these
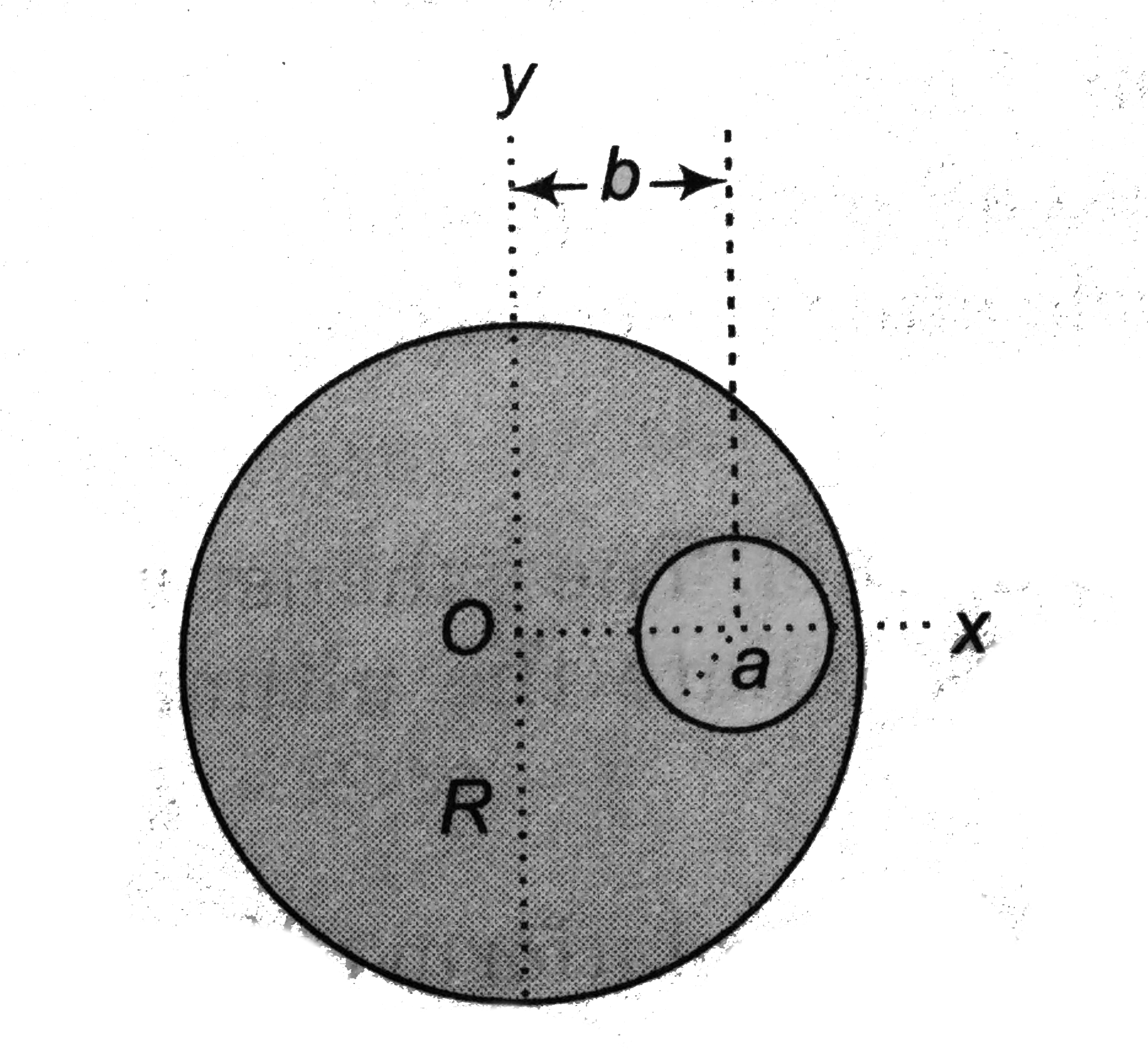
A(0,0)B(0,R)C(0,√3R2)Dnone of theseFind the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
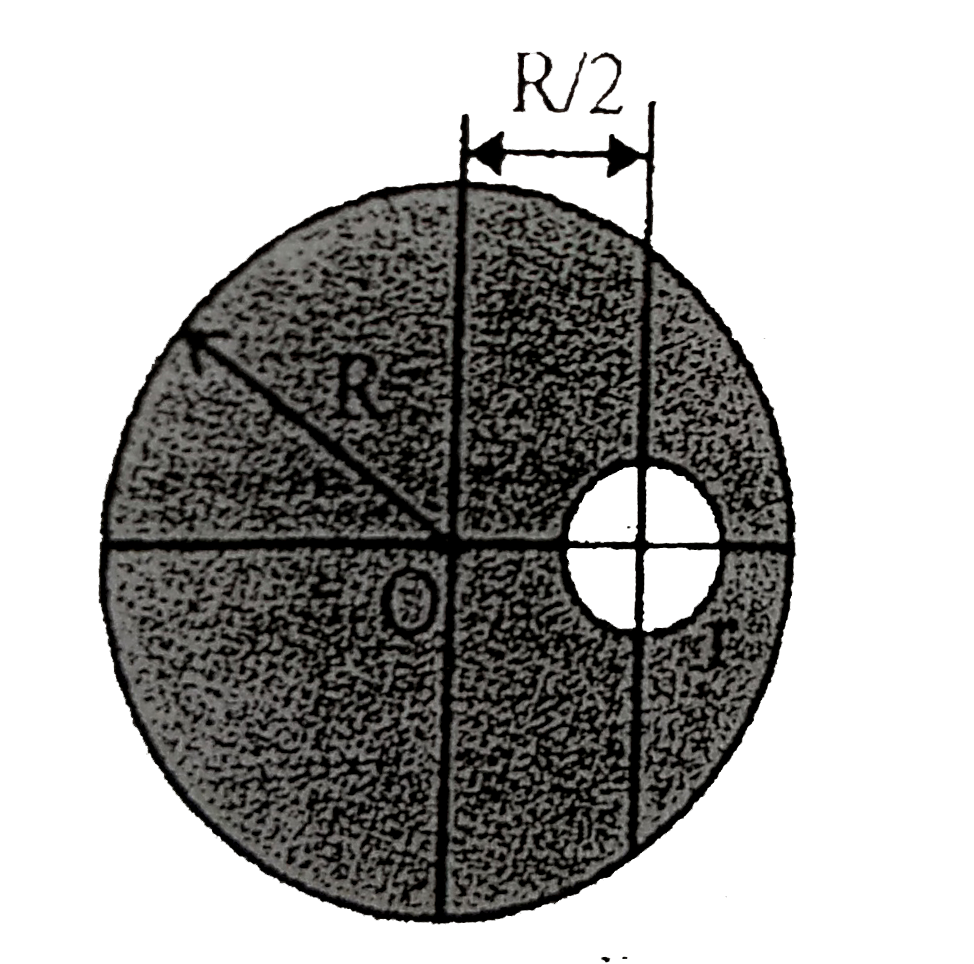 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
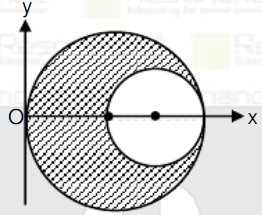
Figure shows a uniform disc of radius R, from which a hole of radius R2 has been cut out from left of the centre and is placed on the right of the centre of the disc. Find the CM of the resulting disc.
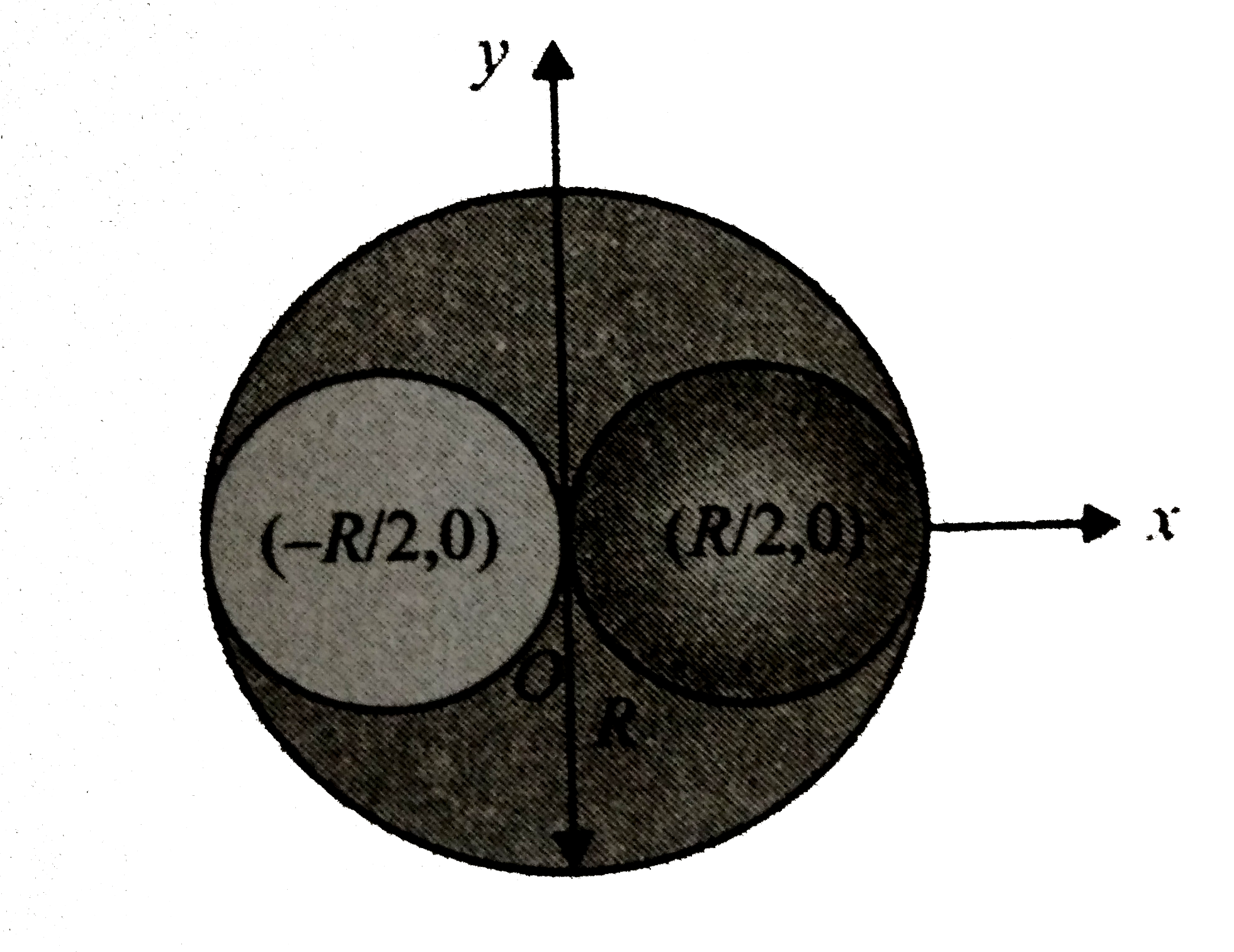
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
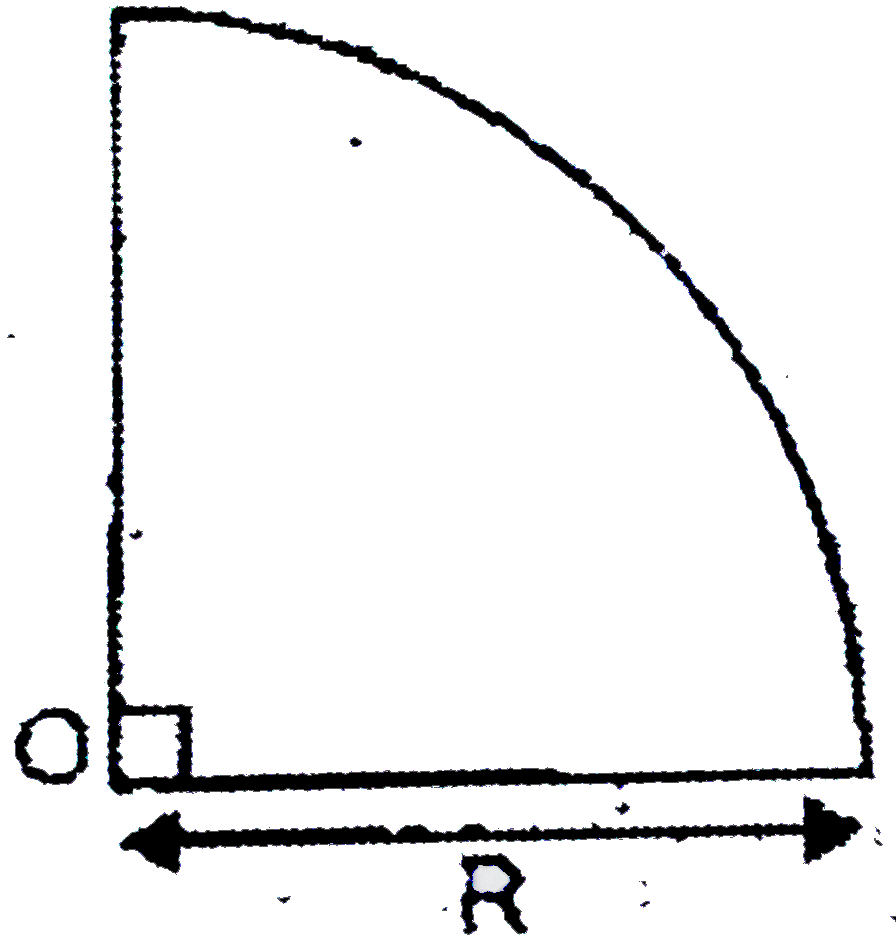
View SolutionIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View SolutionA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
View Solution