A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
335cm
135cm
310cm
None of these
The correct Answer is:A
For the calculation of the position of centre of mass, cut off mass is taken as negative. The mass of disc is
m1=πr21σ=πt2σ=36πσ
where σ= surface mass density. The mass of cut of portion is
m2=π(1)2σ=πσ
xcm=m1x1−m2x2m1−m2
Taking origin at the centre of disc.
x1=0,x2=3cm
xcm=36πσ×0−πσ×336πσ−πσ
=−3πσ35πσ=−335cm
Topper's Solved these Questions
Similar Questions
A disc of radis R is cut out from a larger disc of radius 2R in such a way that the edge of the hole touches the edge of the disc. Locate the centre of mass of the residual disc.
View SolutionFrom a uniform disc of radius R, a circular section of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of mass of the resulating flat body.
View Solution
Knowledge Check
A circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A335cmB135cmC310cmDNone of theseA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)
Aπb2(a2−b2)B−cb2(a2−b2)Cπc2(a2−b2)Dπa2(c2−b2)A uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by
 Aπb2a2−c2Bcb2a2−b2Cπc2a2−b2Dca2(c2−b2)
Aπb2a2−c2Bcb2a2−b2Cπc2a2−b2Dca2(c2−b2)
In the figure shown a hole of radius 2 cm is made in a semicircular disc of radius 6π at a distance 8 cm from the centre C of the disc. The distance of the centre of mass of this system from point C is :

View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA disc of radius r is cut from a larger disc of radius 4r in such a way that the edge of the hole touches the edge of the disc. The centre of mass of the residual disc will be a distance from centre of larger disc :-
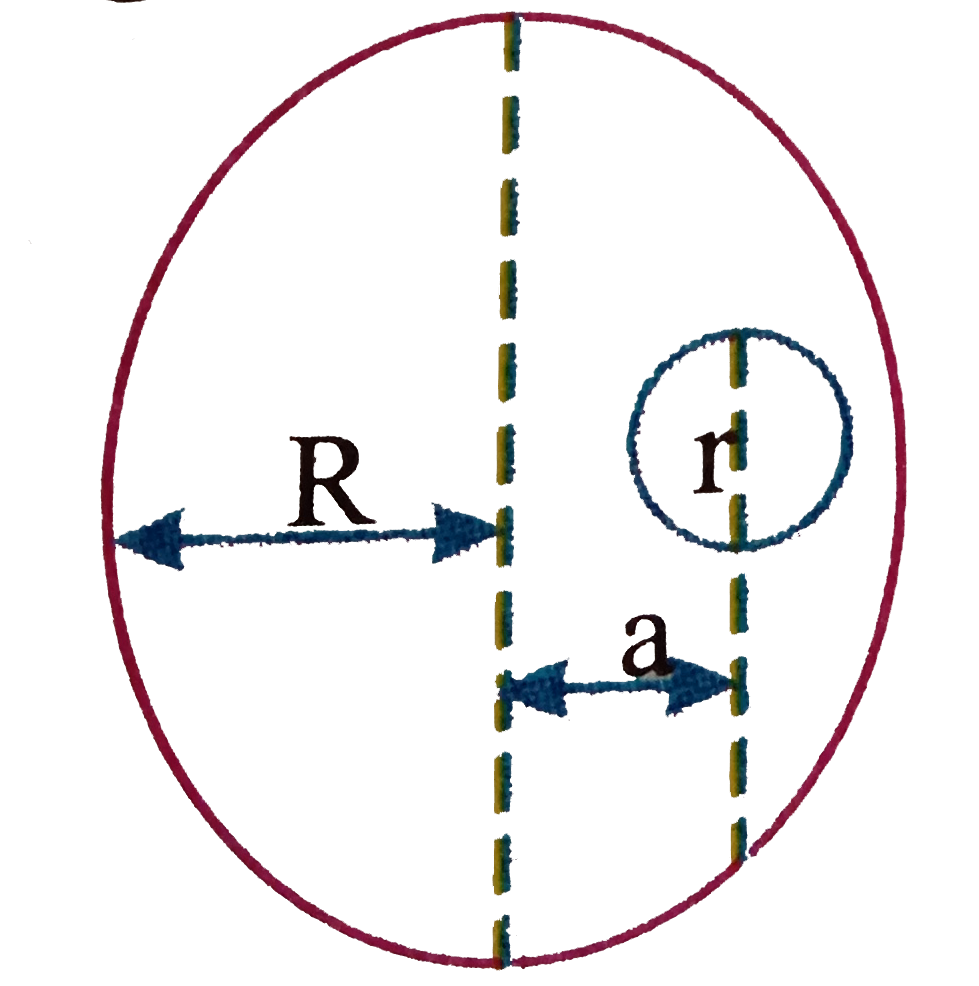
View SolutionA circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
View SolutionA small disc of radius 2cm is cut from a disc of radius 6cm. If the distance their centers is 3.2cm, what is the shift in the center of mass of the disc?
View Solution
