A disc of radius R start at time t=0 moving along the positive X-axis with linear speed b and angular speed ω. Find the x and y-coordinates of the bottommost point at any time t.
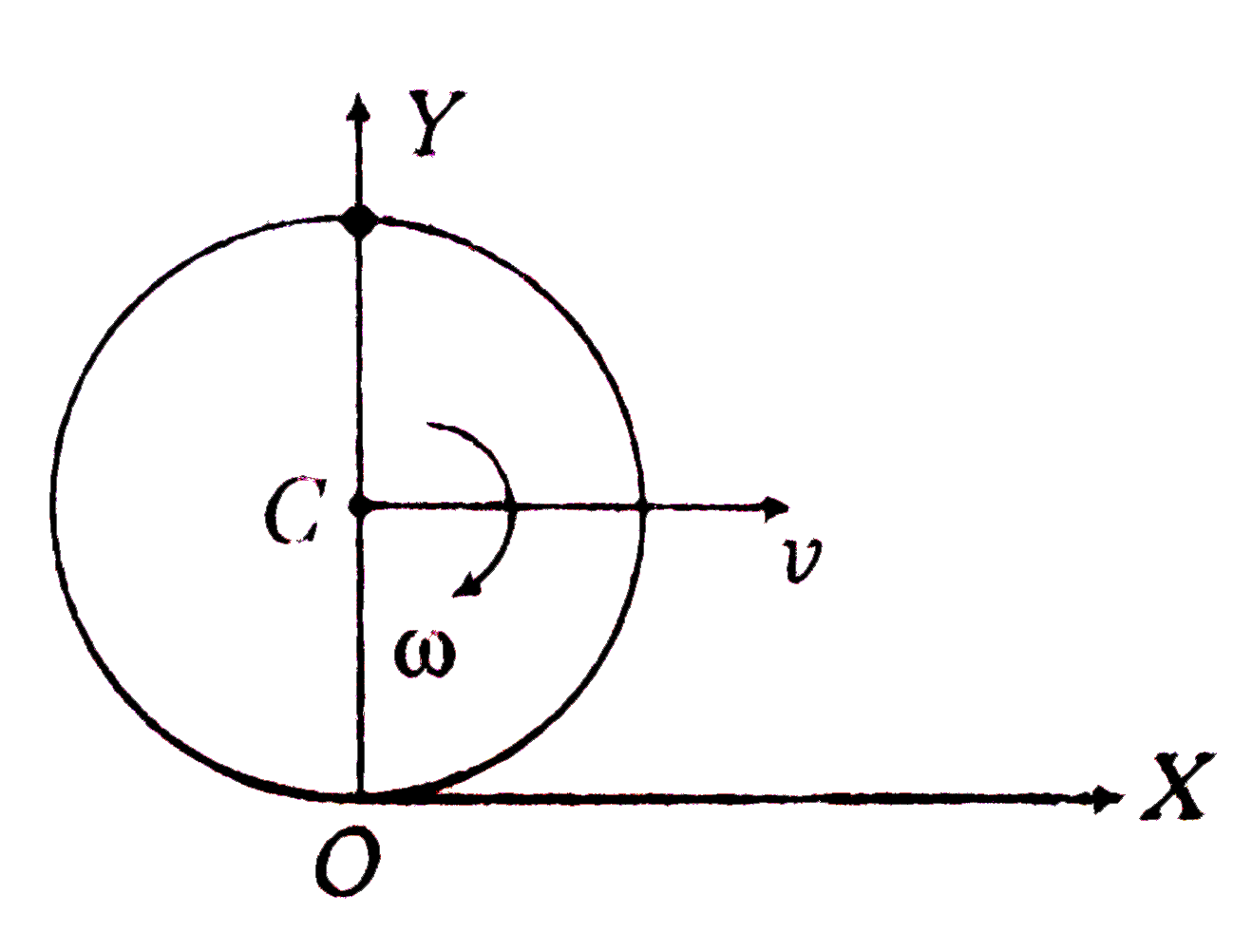
At time t, the bottommost point will rotate an angle θ=ωt with respet to the centre of the disc c. The centre C will travel a distance s=vt
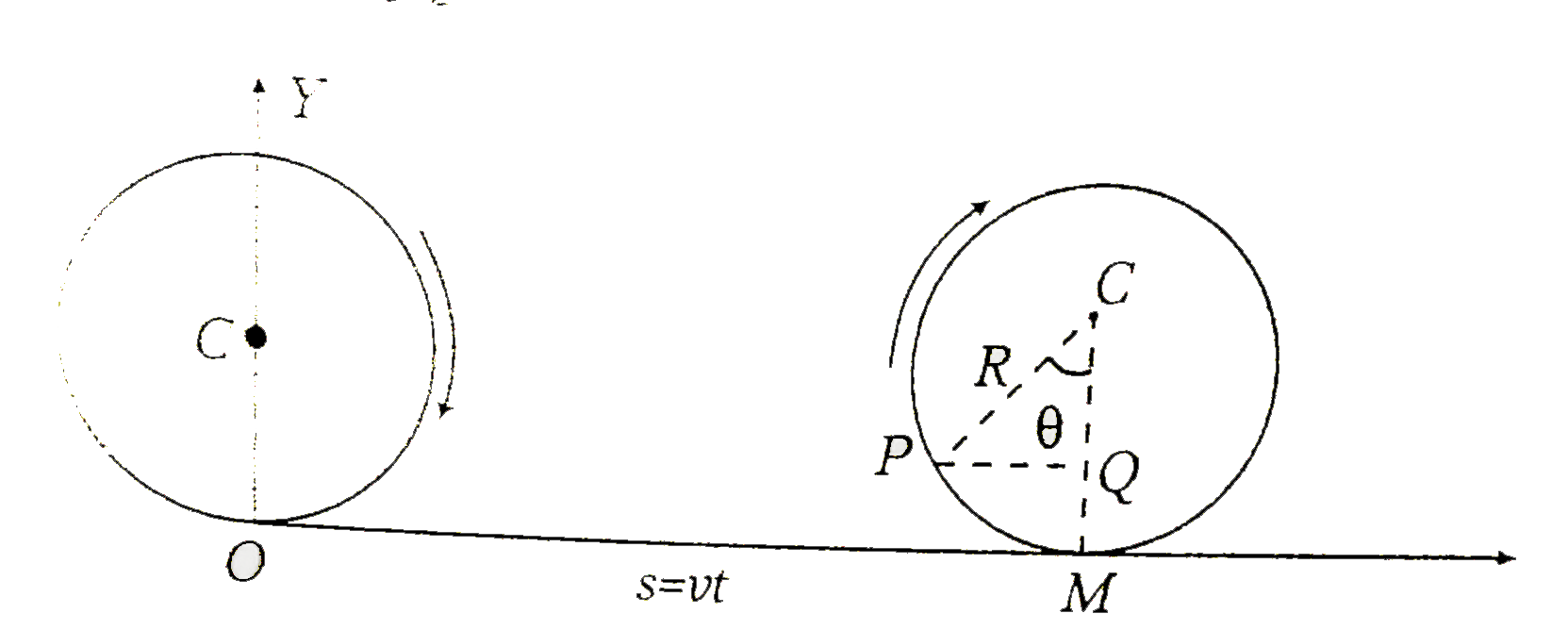
In the figure , PQ=Rsinθ=Rsinωt
and CQ=Rcosθ=Rcosωt
Coordinates of points P and at time t are,
x=OM−PQ=vt−Rsinωt
and y=CM−CQ=R−Rcosωt
∴(x,y)≡(vt−Rsinωt,R−Rcosωt)
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
Combined Rotational & Translational Motion|Questions|x And y Coordinates Of The Bottommost Point At Any Time t.
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?
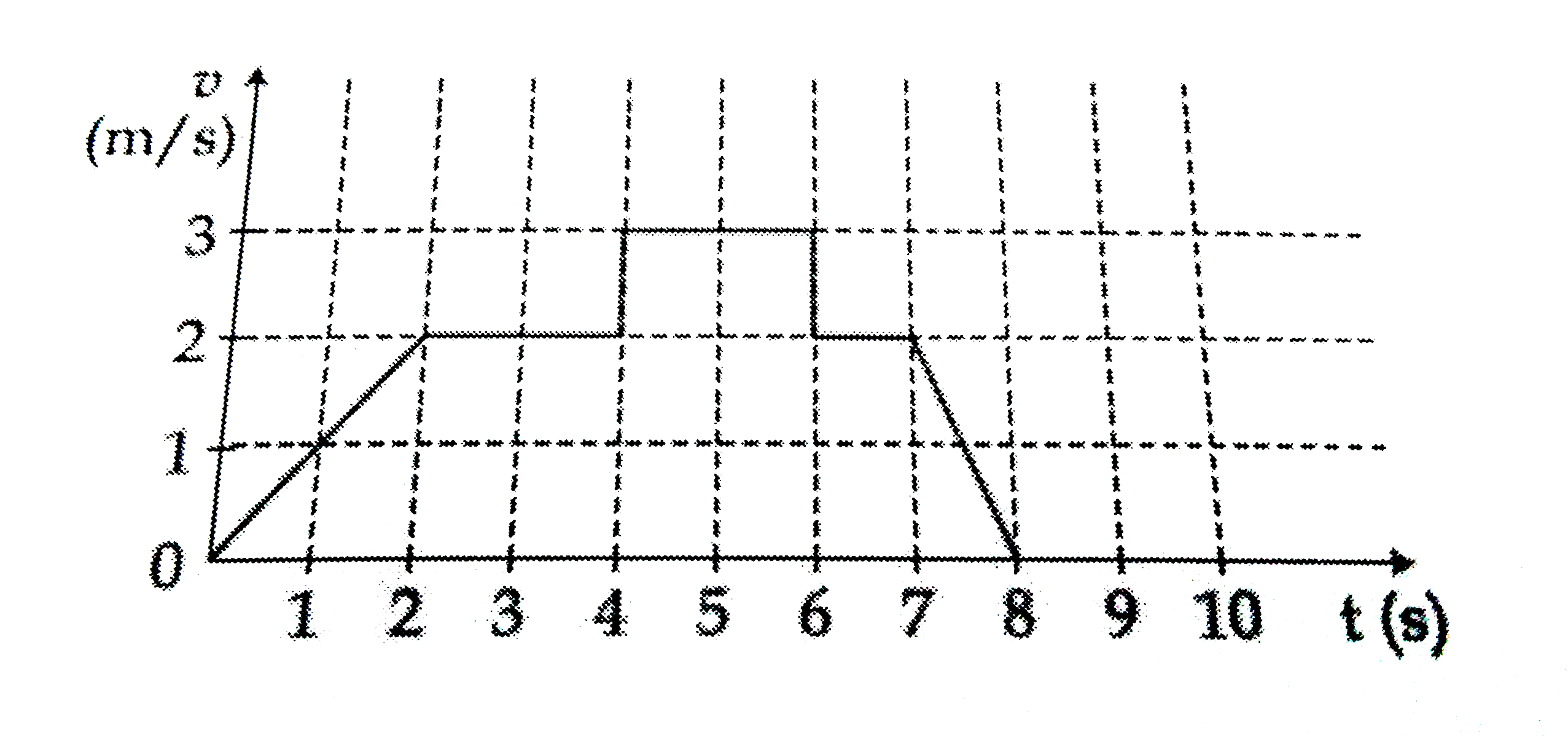
View Solution
Knowledge Check
Two identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
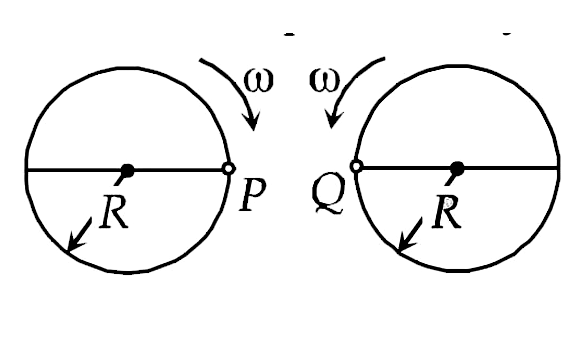 A
A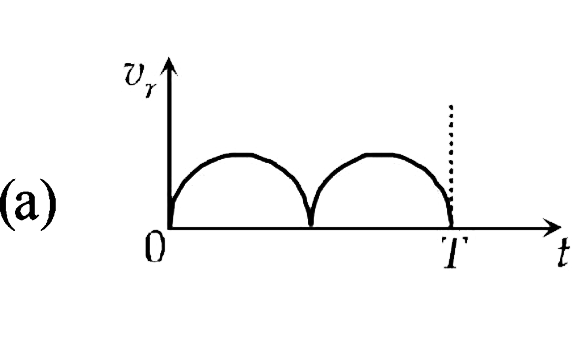 B
B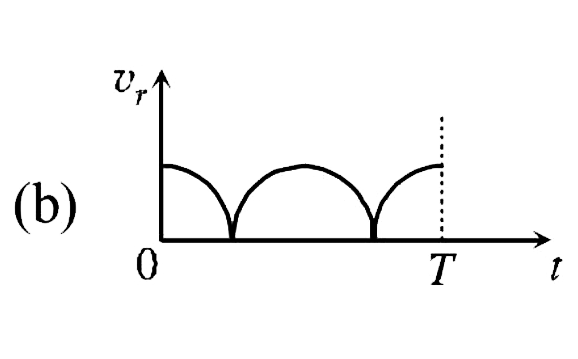 C
C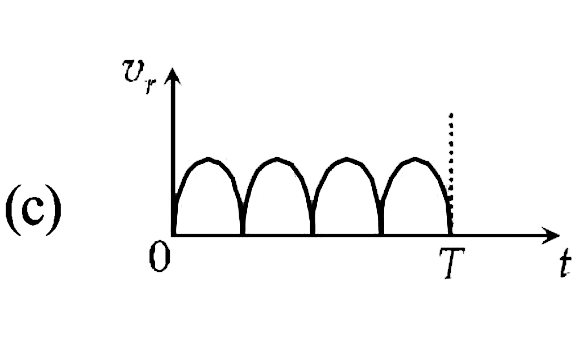 D
D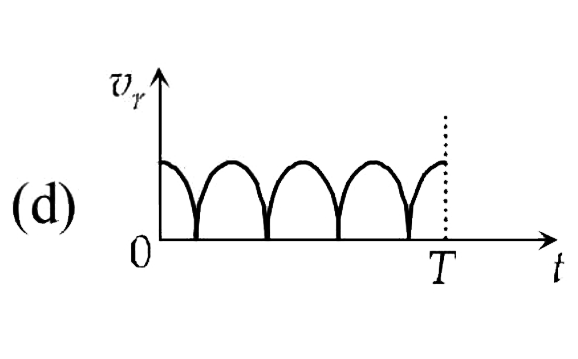
A particle moves along a circle of radius R with a constant angular speed ω. Its displacement (only magnitude) in time t will be
AωtB2RcosωtC2RsinωtD2Rsin.ωt2A particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
AωtB2RcosωtC2RsinωtD2Rsinωt2
A disc of radius 10 cm is rotating about its axis at an angular speed of 20 rad/s. Find the linear speed of
a. a point on the rim,
b. the middle point of a radius.
View Solution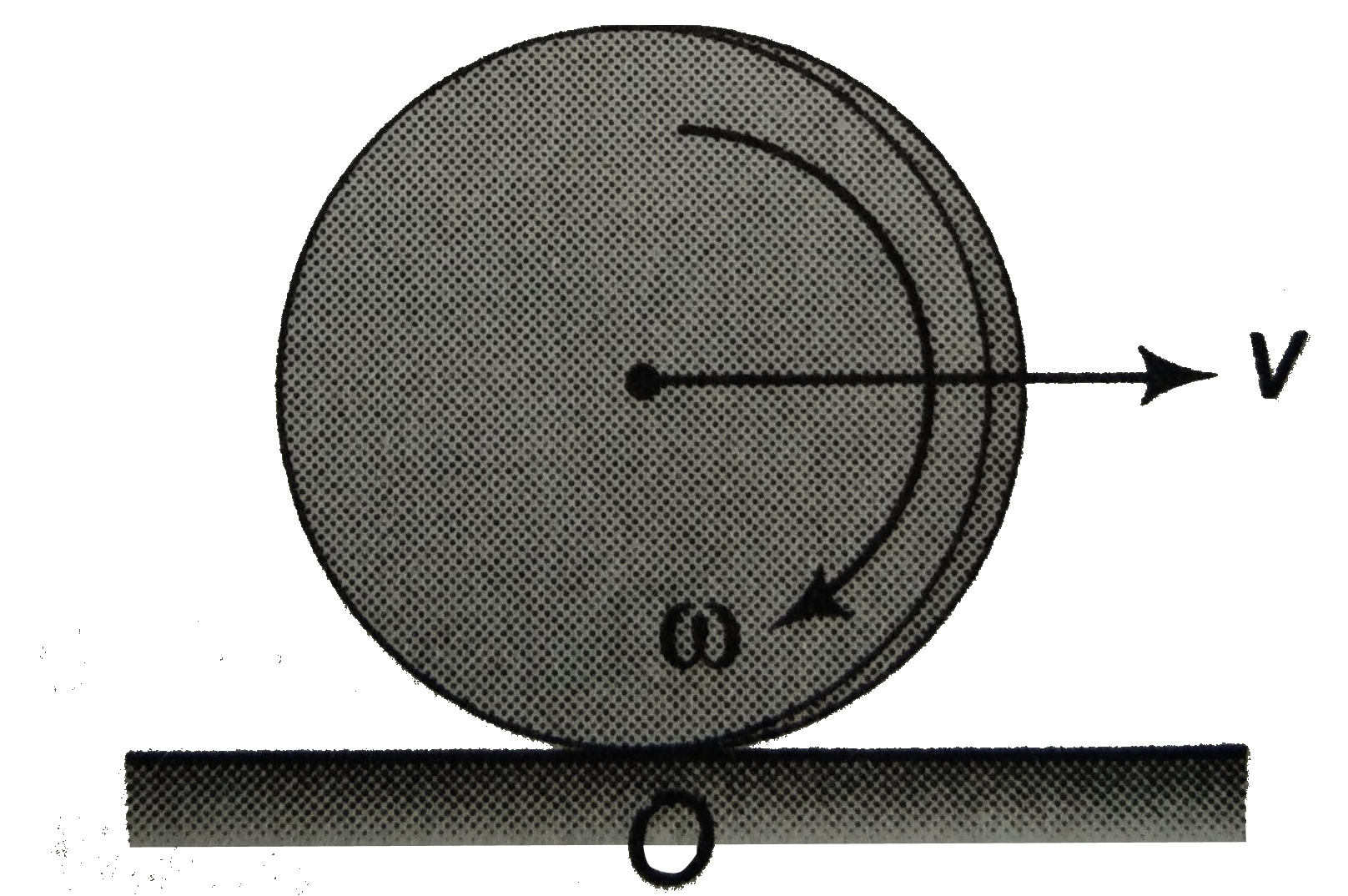
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View SolutionThe magnitude of displacement of a particle moving in a circle of radius a with constant angular speed ω varries with time t is
View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA particle is moving on a circular path of radius R with uniform angular speed ω. The magnitude of average velocityof particle during time t=0 to t=2π3ω:
View Solution
