A diver at a depth of 12 m in water (μ=4/3) sees the sky in a cone of semi-vertical angle
sin−1(43)
tan−1(43)
sin−1(34)
90∘
We can represent this diagrammatically as,

Thus, we see that C=sin−1(1μ)=sin−1(34)
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:REFRACTION OF LIGHTExercise:Exercise 2
Explore 25 Videos
- REFRACTION OF LIGHTBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:REFRACTION OF LIGHTExercise:Exercise 2
Explore 25 Videos
- RAY OPTICSBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:RAY OPTICSExercise:EXERCISE 2 (MISCELLANEOUS PROBLEMS)
Explore 19 Videos
- ROTATIONAL MOTION'Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:ROTATIONAL MOTION'Exercise:MHT CET Corner
Explore 35 Videos
Similar Questions
A ship is salling in river. An observe is situated at a depth h in water (μw). If x>>h, find the angle made form vertical, of the line of slight of ship.

View SolutionWater is dropped at the rate of 3m3sec into a cone of semi vertical angle 30∘ .Then the rate at which periphery of water surface changes, when height of water in the cone is 3m ,is
View Solution
Knowledge Check
A water tank has the shape of an inverted right circular cone, whose semi-vertical angle is tan−1(12). Water is poured into it at a constant rate of 5 cu m/min. Then, the rate (in m/min) at which the level of water is rising at the instant when the depth of water in the tank is 10 m is
A2πB15πC115πD110πIf the real depth of a coin in water (μ = 4/3) is 4 cm, the apparent depth is
A3 cmB13 cmC163DNone of theseA ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle 45∘ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is r(r<<R).
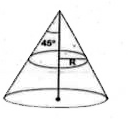
What will be the tension in the ring?Amg2√2πBmg2πCmg√2πD√2mgπ
Water is dropped at the rate of 3m3/sec into a cone of semi vertical angle 30∘ Then the rate at which periphery of water surface changes, when height of water in the cone is 3m is
View SolutionWater is dropped at the rate of 2 m3/s into a cone of semi-vertical angle is 45∘ . If the rate at which periphery of water surface changes when the height of the water in the cone is 2m is d. Then the value of 5d is _____ m/sec
View SolutionFor a fish under water, the entire outside view is confined within a cone. Draw an appropriate ray diagram for this and calculate the value of semi-vertical angle of the cone. Refractive index of water =4/3
View SolutionA ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle 45∘ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is r(r<<R).
What will be the speed of transverse wave on the ring?
View SolutionA fish at a depth of 12cm in water is viewed by an observer on the bank of a lake. To what height the images of the fish is raised ?
View Solution