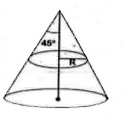
A ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle $45^{\circ}$ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is $r (r < < R)$ .

What will be the speed of transverse wave on the ring?

A

$\sqrt{g R}$

B

$\sqrt{2 g R}$

C

$\frac{1}{2} \sqrt{g R}$

D

$2 \sqrt{g R}$

Text Solution

Verified by Experts

The correct Answer is:A

$v = \sqrt{\frac{T}{μ}} = \sqrt{\frac{m g}{2 π (\frac{m}{2 π R})}} = \sqrt{g R}$

|

Updated on:21/07/2023

Class 12 PHYSICS LAWS OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A ring of mass m and radius R rests in equilibrium on a smooth cone of semi-vertical angle $45^{\circ}$ as shown. The radius of the cone is 2R. the radius of circular cross section of the ring is $r (r < < R)$ .

What will be the tension in the ring?
A $\frac{m g}{2 \sqrt{2} π}$
B $\frac{m g}{2 π}$
C $\frac{m g}{\sqrt{2} π}$
D $\frac{\sqrt{2} m g}{π}$
Question 2 - Select One
For a uniform ring of mass M and radius R at its centre
Afield and potential both are zero
Bfield is zero but potential is $\frac{G M}{R}$
Cfield is zero but potential is $- G M / R$
Dmagnitude of field is $\frac{G M}{R^{2}}$ and potential $- \frac{G M}{R}$
Question 3 - Select One or More
A unifrom metallic ring of mass $m$ , radisus $R$ , cross sectional area $' a'$ and young'/s modulus $Y$ kis kept on a smooth cone of radius $2 R$ and semivertex angle $45^{\circ}$ as shown. [Assume that extension in the ring is small]

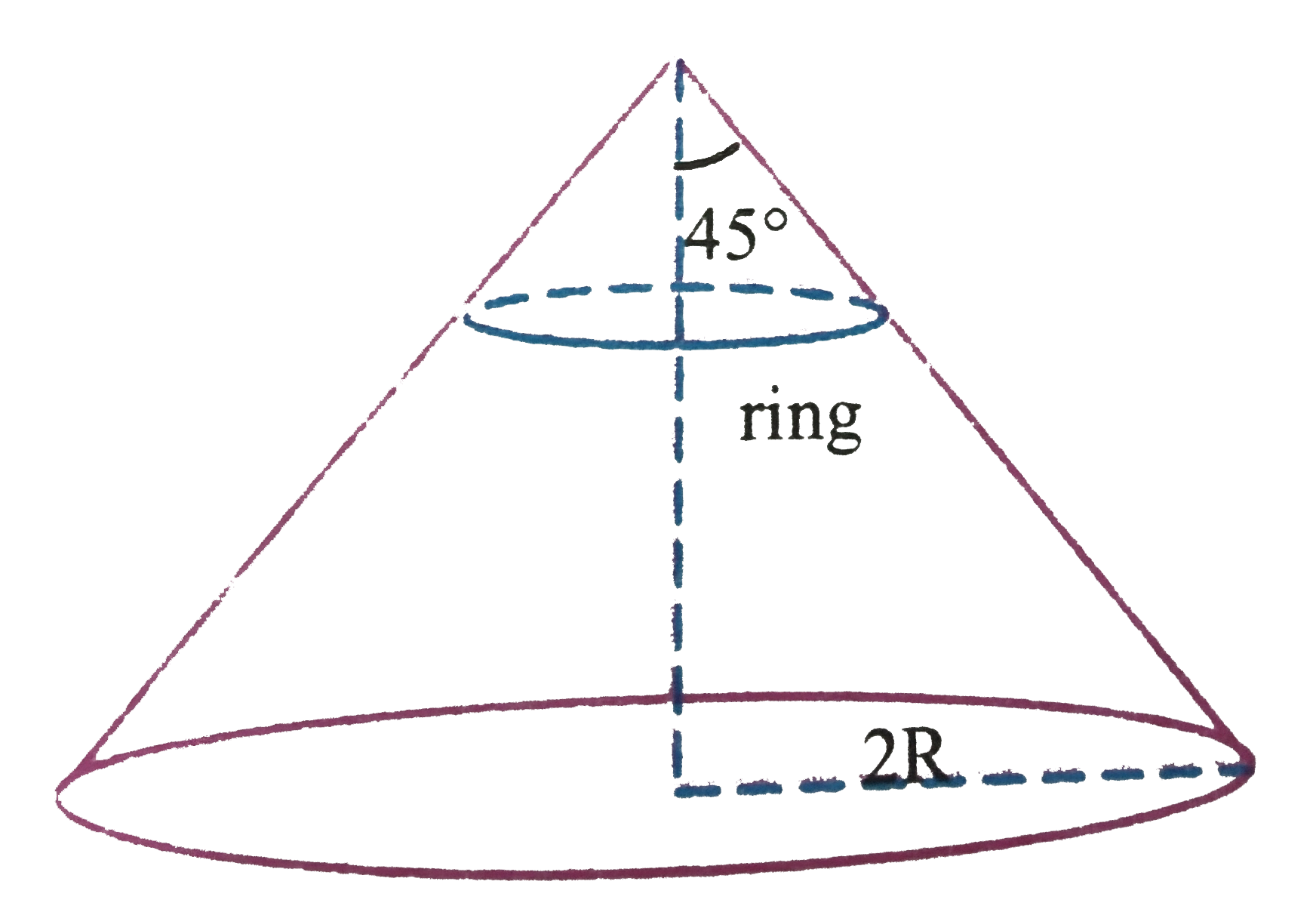AThe tension in the ring will be same through out
BThe tension in the ring will be independent of radius of ring.
CThe extension in the ring will be $\frac{m g R}{a Y}$
DElastic potential energy should in the ring will be $\frac{m^{2} g^{2} R}{8 π Y a}$

FIITJEE-LAWS OF MOTION-COMPREHENSION - II

Home
Ask Doubt
Profile