A double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
22.86 same side of the object
22.86 opposite side of the object
44.89 same side of the object
44.89 opposite side of the object.
The correct Answer is:A
To find the position of the image formed by a double convex lens, we can follow these steps:
Step 1: Identify the Given Values
- Refractive index of the lens, n=1.56
- Radii of curvature, R1=+20cm (since it is convex, we take it as positive)
- R2=−20cm (the second radius is negative for a double convex lens)
- Object distance, u=−10cm (the object distance is negative as per the sign convention)
Step 2: Use the Lensmaker's Formula
The Lensmaker's formula is given by:
1f=(n−1)(1R1−1R2)
Substituting the values into the formula:
1f=(1.56−1)(120−1−20)
Calculating the right-hand side:
1f=0.56(120+120)=0.56(220)=0.56(110)=0.5610=0.056
Thus,
f=10.056≈17.86cm
Step 3: Use the Lens Formula to Find Image Distance
The lens formula is given by:
1f=1v−1u
Rearranging to find v:
1v=1f+1u
Substituting the values we found:
1v=117.86+1−10
Calculating each term:
117.86≈0.056and1−10=−0.1
Now substituting these values:
1v=0.056−0.1=−0.044
Thus,
v=1−0.044≈−22.72cm
Step 4: Interpret the Result
The negative sign indicates that the image is formed on the same side as the object. Therefore, the position of the image is approximately 22.72cm on the same side as the object.
Final Answer
The position of the image formed is −22.72cm (same side as the object).
---
- Refractive index of the lens, n=1.56
- Radii of curvature, R1=+20cm (since it is convex, we take it as positive)
- R2=−20cm (the second radius is negative for a double convex lens)
- Object distance, u=−10cm (the object distance is negative as per the sign convention)
The Lensmaker's formula is given by:
The lens formula is given by:
The negative sign indicates that the image is formed on the same side as the object. Therefore, the position of the image is approximately 22.72cm on the same side as the object.
The position of the image formed is −22.72cm (same side as the object).
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
View SolutionA double convex thin lens made of glass (refractive index μ=1.5) has both radii of curvature of magnitude 20 cm . Incident light rays parallel to the axis of the lens will converge at a distance L such that
View Solution
Knowledge Check
A double convex lens is made of glass of refractive index 1.55 with both faces of same radius of curvature. Find the radius of curvature required, if focal length is 20cm.
A11cmB22cmC7cmD6cm
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the image
View SolutionA double convex thin lens made of glass of refractive index 1.6 has radii of curvature 15 cm each. The focal length of this lens when immersed in a liquid of refractive index 1.63 is :
View SolutionA biconvex lens is made of glass with refractive index 1.5 and has radii of curvature 20 cm and 30 cm. If the 20 cm surface is silvered, what is the effective focal length of the mirror formed?

View SolutionA biconvex lens separates two media of refractive indices 1.3 and 1.7. the refractive index of the lens is 1.5 and the radii of curvature of the two sides of the lens are r1=10cm and r2=60cm .
The medium of refractive index 1.3 extends to 78 cm from the lens and that of refractive index 1.7 extends of 34 cm from the lens. A luminous object O is at a distance of 144 cm from the lens. Find the position of the final image from the lens.
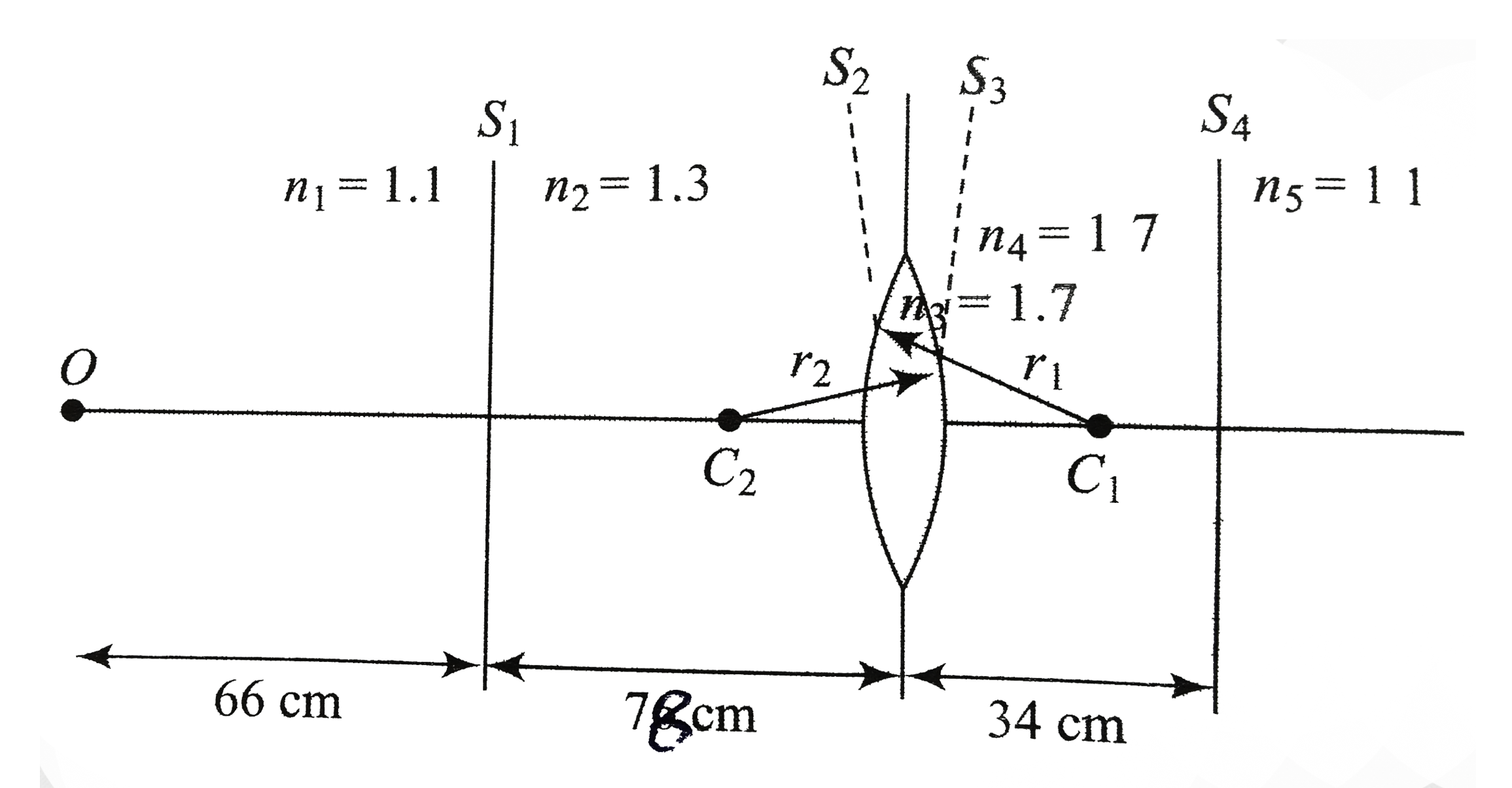
View SolutionA double convex lens is made of glass of refractive index 1.55 with both faces of same radius of curvature. Find the radius of curvature required, if focal length is 20cm.
View SolutionA double convex lens is made of glass of refractive index 1.55 with both faces of same radius of curvature. Find the radius of curvature required, if focal length is 20cm.
View SolutionA convex mirror has its radius of curvature 20 cm. Find the position of the image of an object placed at a distance of 12 cm from the mirror.

View Solution
