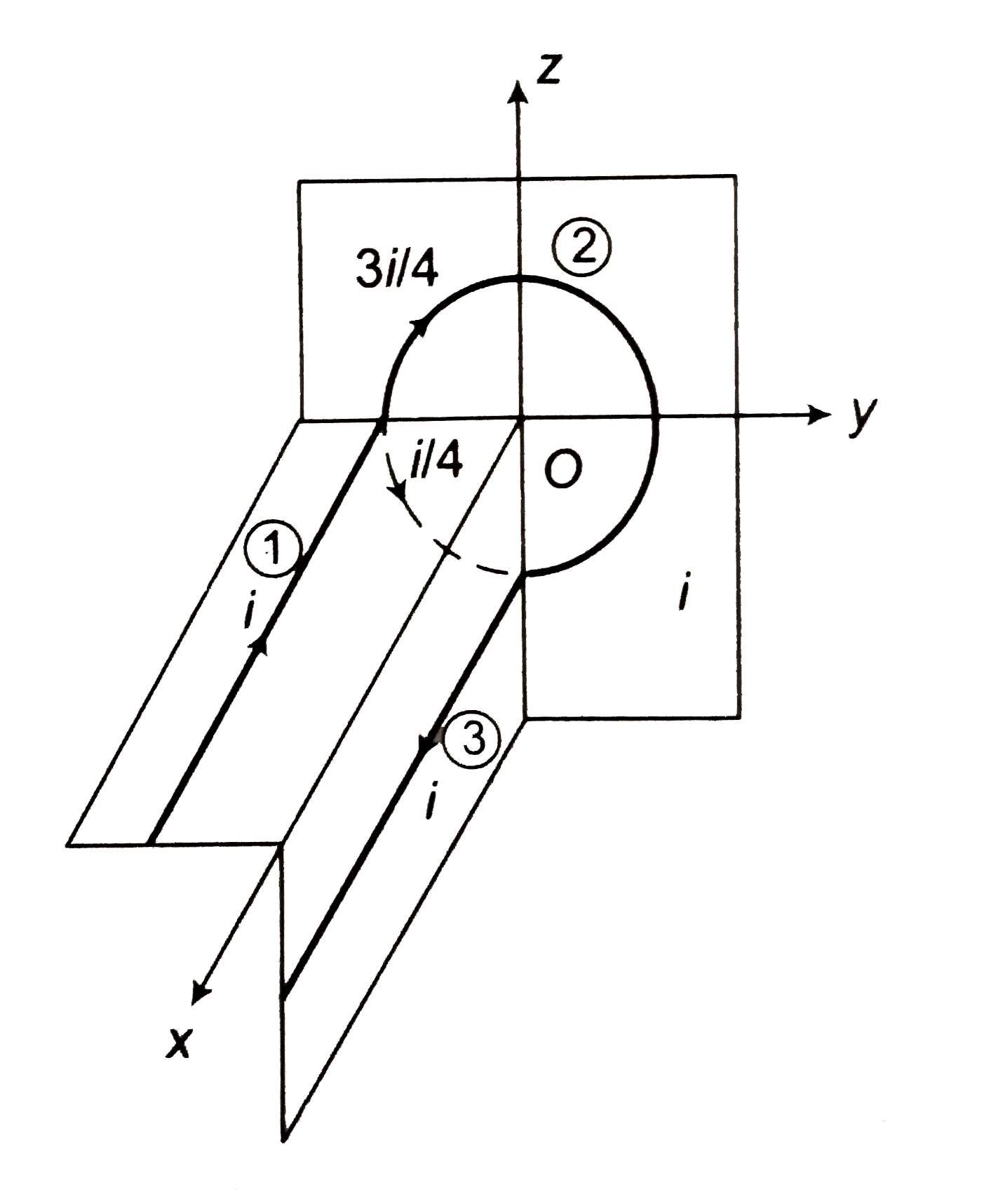
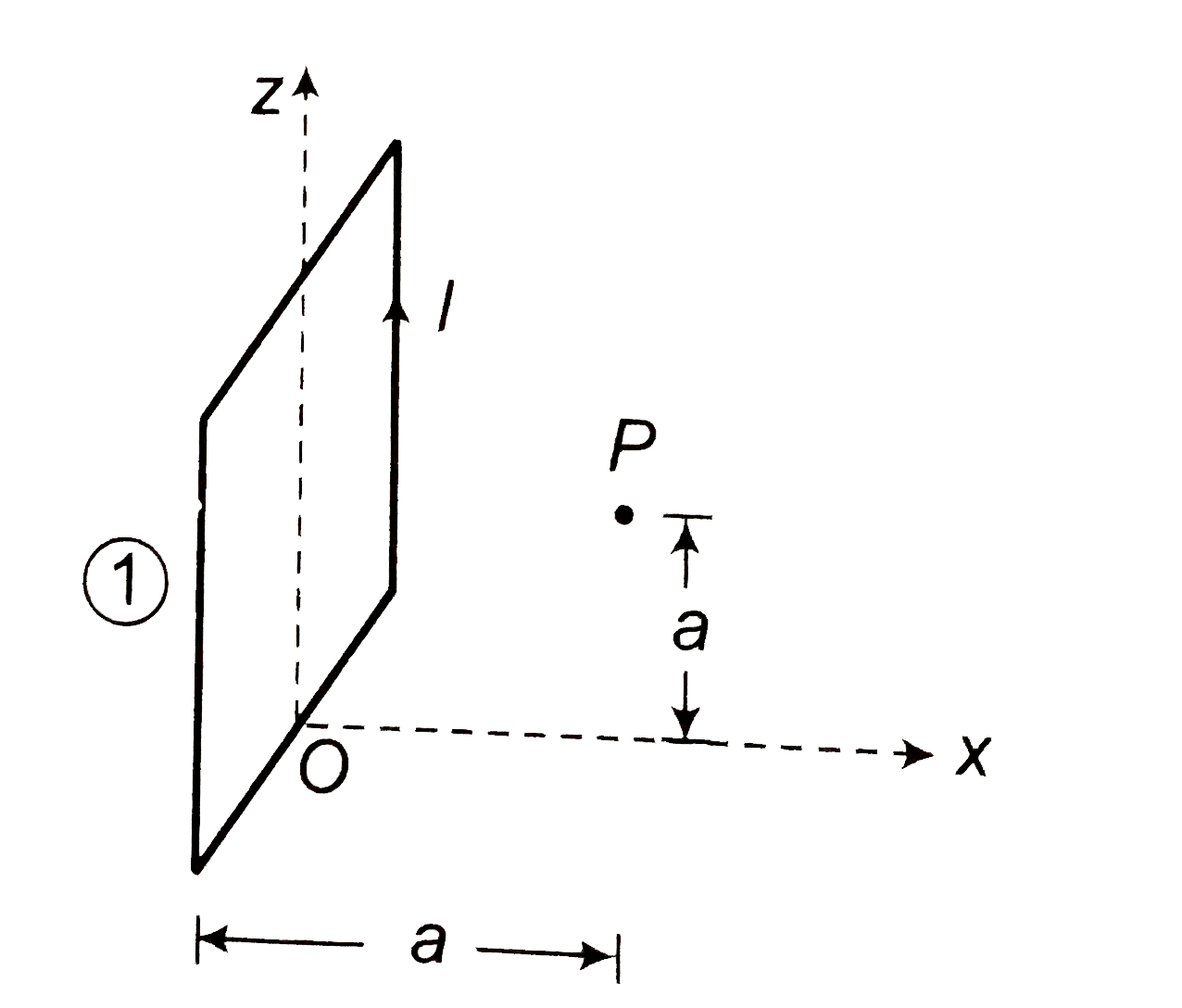
(a) Find the magnetic field at the point O if the wire carrying a current i has the shape shown. The radius of the current part of the wire is R, the linear parts of the wire are very long.
(i) 
(ii) 
(iii) 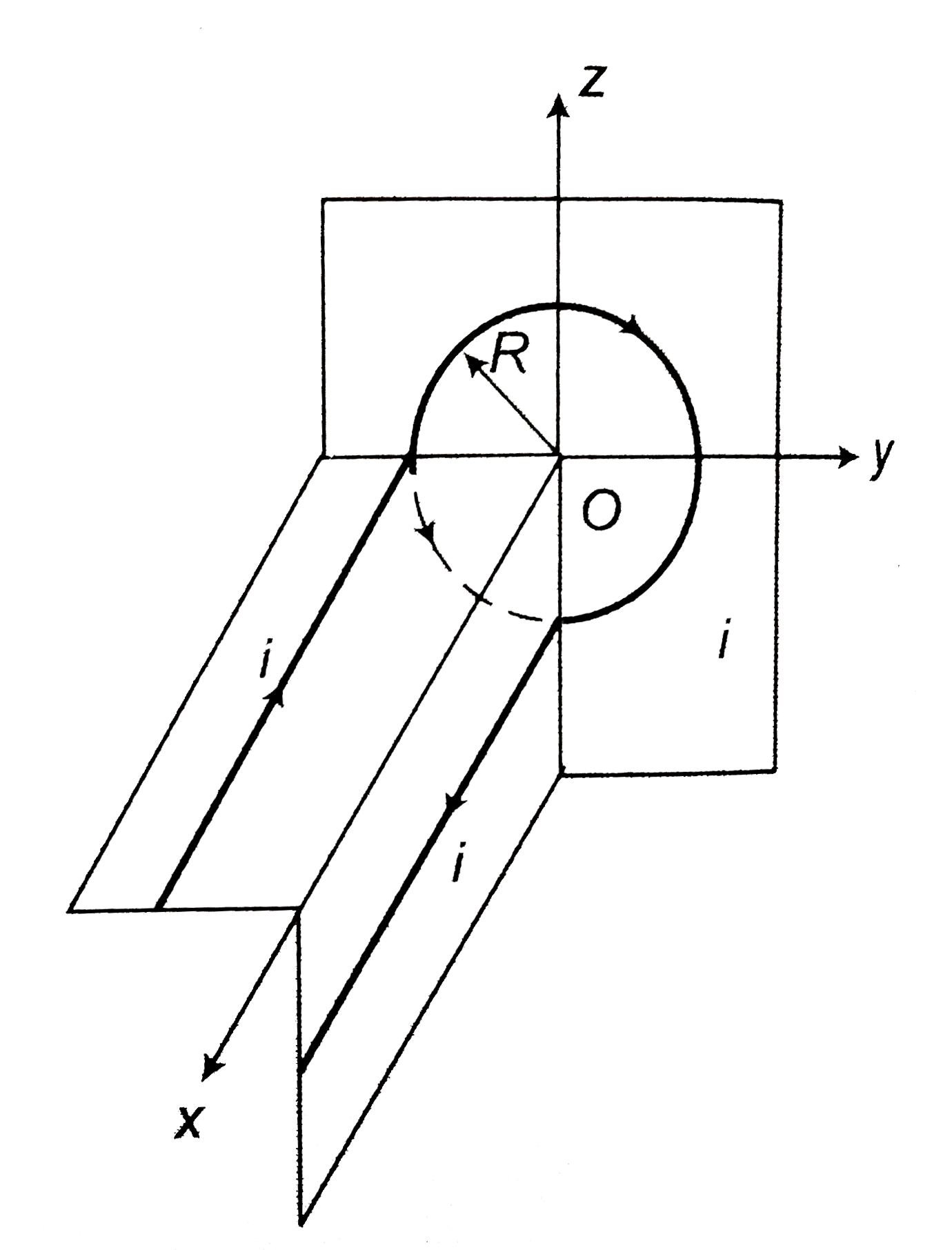
(b) A long straight wire along the z-axis carriers a current i in negative z-direction. Find magnetic field in vector from at a point having co-ordinates (x,y) on z=0 plane.
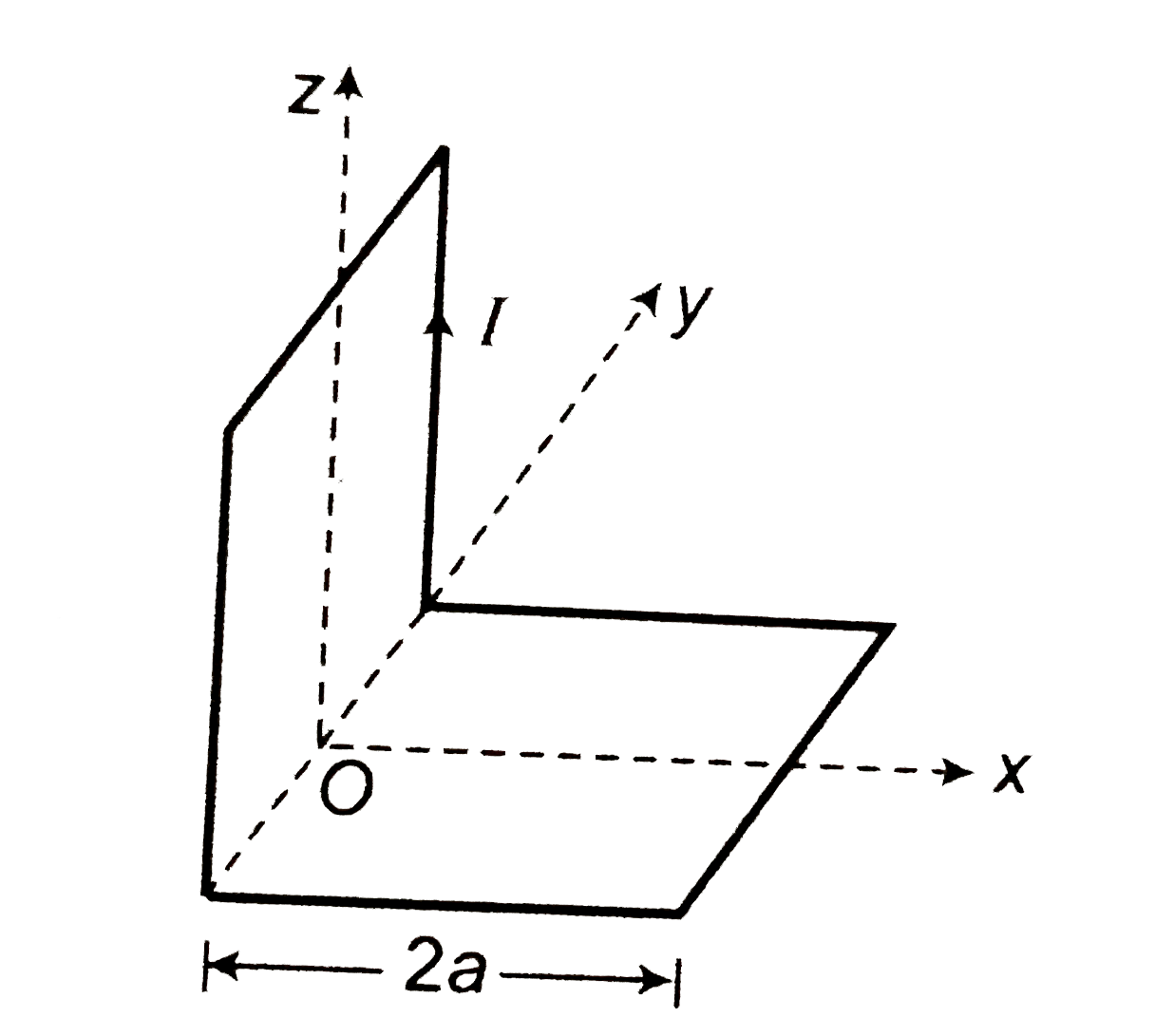
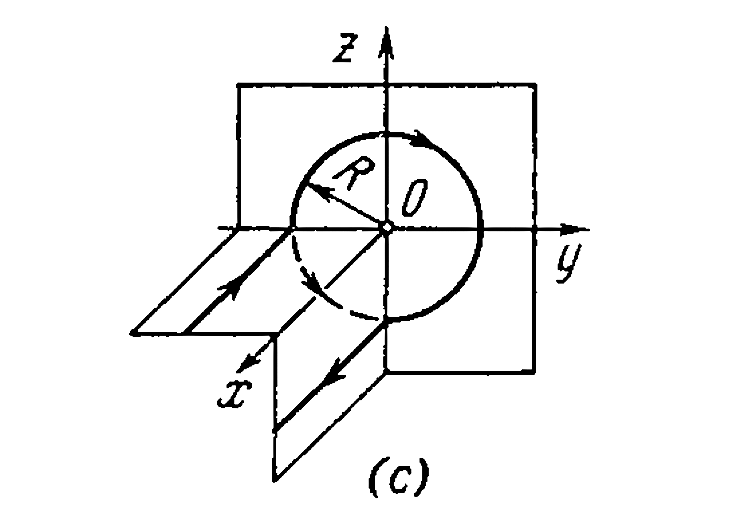
(c) A non-coplaner loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop of length 2a. find unit vector along magnetic field magnetic filed at the point P(a,0,a).
(a) (i) 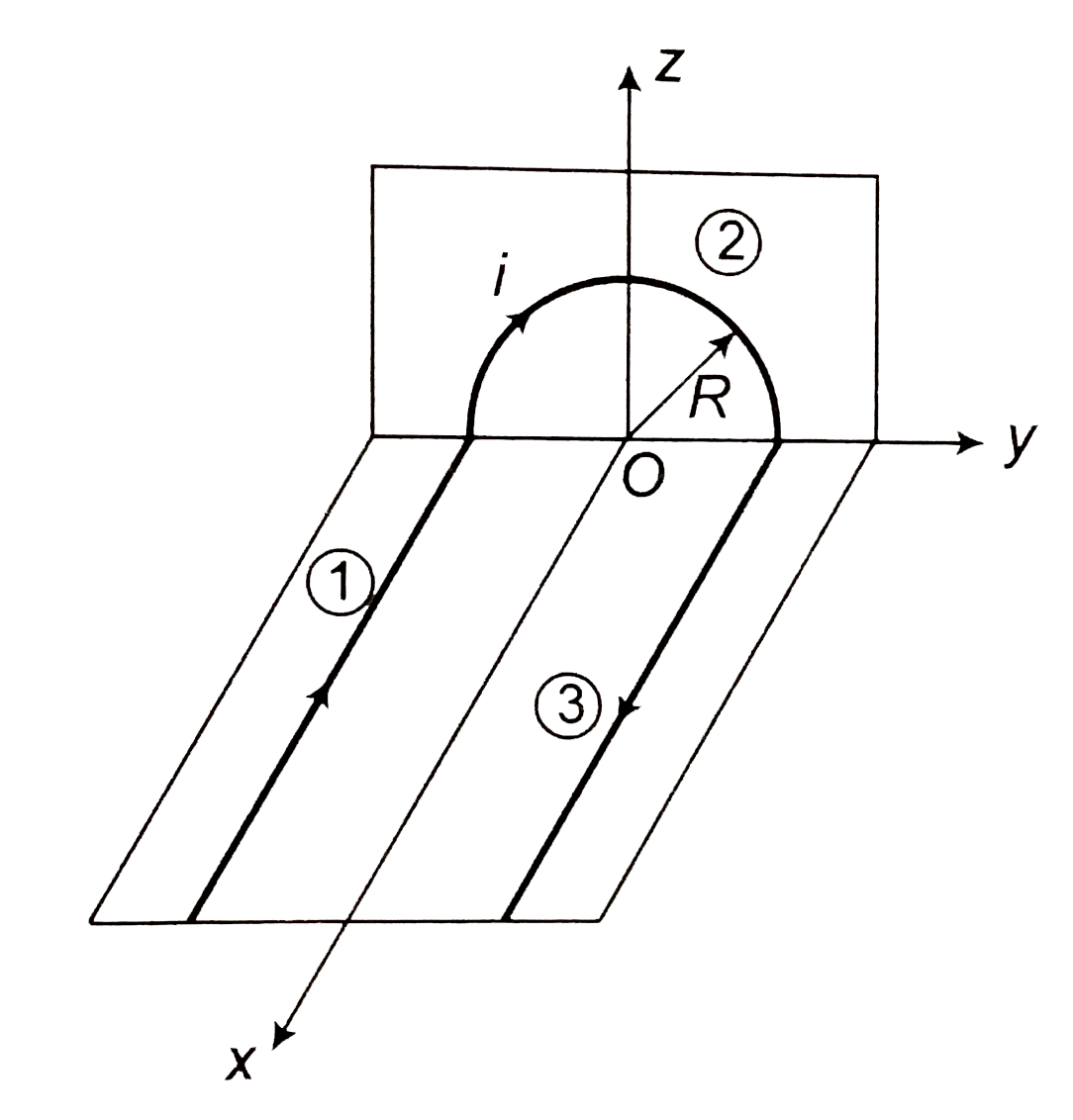
At O:
Wire ① is in x−y plane.
Magnetic field due to this wire be ⊥ar to plane x−y at O.
B1=μ0i4πR, along z-axis
Wire ② is in y−z plane.
B2=μ0i4R, along −x-axis
B3=μ0i4πR, along −z-axis
→BO=−(B1+B3)ˆk−B2ˆi
=−μ0i4Rˆi−μ0i2πRˆk
∣∣→B∣∣=Bo=μ0i4R√1+(2π)2
(ii) 
B1=μ0i4πR, along −z axis
B2=μ0i4R, along −x axis
B3=μ0i4πR, along −x axis
→BO=−(B2+B3)ˆi−B3ˆk
=−(μ0i4R+μ0i4πR)ˆi−μ04πRˆk
∣∣→BO∣∣=BO=μ0i4R√(1+1π)2+(1π)2
(iii)
B1=μ0i4πR, along −zdirection
B2=0, current is divided in two parts and magnetic field due to these parts is zero.
B3=μ0i4πR, along −y direction
→BO=−B3ˆj−B1ˆk
=−μ0i4πRˆj−μ0i4πRˆk
∣∣→BO∣∣=BO=√2μ0i4πR=μ0i2√2πR
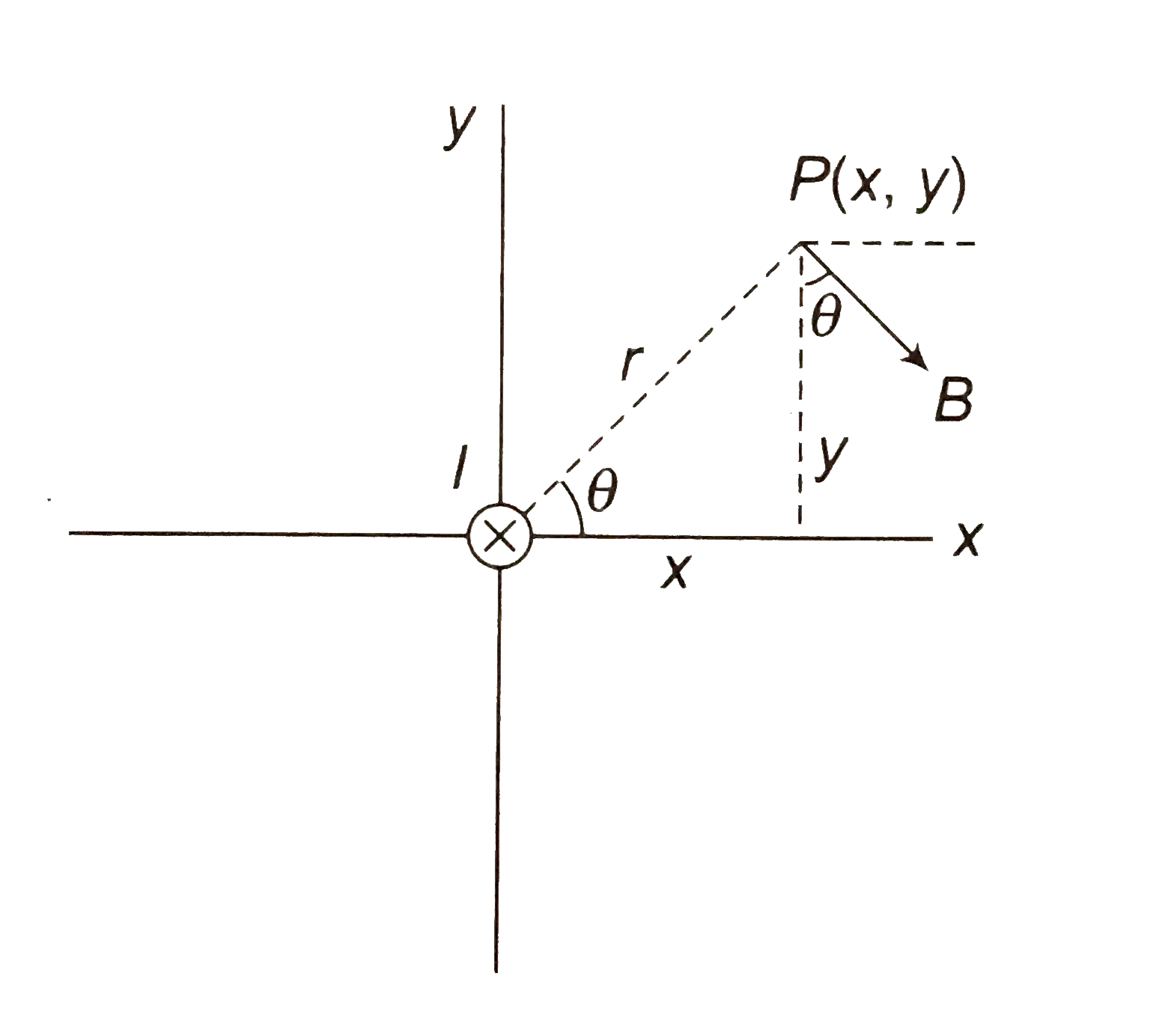
Due to long wire, magnetic field at P is
B=μ0I2πR
→B=Bxˆi−Byˆj
=Bsinθˆi−Bcosθˆj
=B(yrˆi−xrˆj)
=μ0I2πr(yrˆi−xrˆj)
=μ0I2πr2(yˆi−xˆj)
=μ0I2π(x2+y2)(yˆi−xˆj)
(c) There can be two closed loops.
Magnetic field at P due to loop, since is anticlockwise, hence magnetic field will be towards the observer i.e. along =x axis
→B1=Bˆk
where B: magnitude of magnetic field due to each loop.
→BP=→B1+→B2=Bˆi+Bˆk
Unit vector along magnetic field at P
ˆBP=→BP∣∣→BP∣∣=Bˆi+Bˆk√2B=1√2(ˆi+ˆk)
(##CPS_V02_C05_S01_008_S06##)
Topper's Solved these Questions
Similar Questions
Find the magnetic induction at the point O if the wire carrying a current I=8.0A has the shwon in Fig.


The radius of the curved part of the wire is R=100mm, the linear parts of the wire are very long.
View SolutionCalculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)
View Solution
Knowledge Check
A long straight wire along the z−aξs carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
Aμ0I(yˆi)−xˆj2π(x2+y2)Bμ0I(xˆi)+yˆj2π(x2+y2)Cμ0I(xˆj)−yˆi2π(x2+y2)Dμ0I(yxˆi)−yˆj2π(x2+y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
Aμ0I(yˆi−xˆj)2π(x2+Y2)Bμ0I(xˆi+yˆj)2π(x2+Y2)Cμ0I(xˆj−yˆi)2π(x2+Y2)Dμ0I(xˆi−yˆj)2π(x2+Y2)A long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field B at a point having coordinate (x,y) on the z=0 plane is:
Aμ0I(yˆi−xˆj)2π(x2+y2)Bμ0I(xˆi+yˆj)2π(x2+y2)Cμ0I(xˆj−yˆi)2π(x2+y2)Dμ0I(xˆi−yˆj)2π(x2+y2)
Calculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
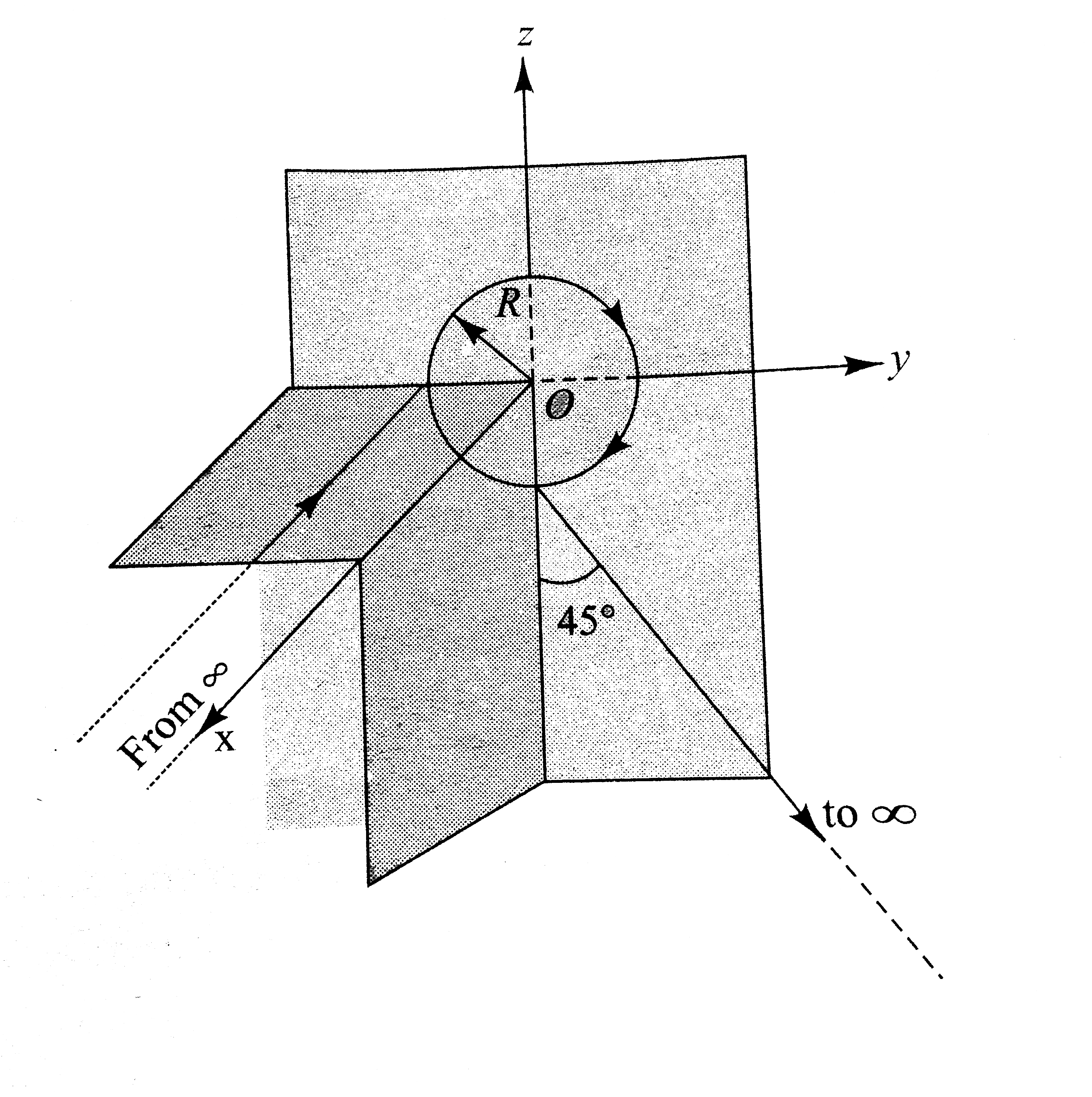
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)
View SolutionCalculate magnetic induction at point O if the wire carrying
a current I has the shape shown in Fig.
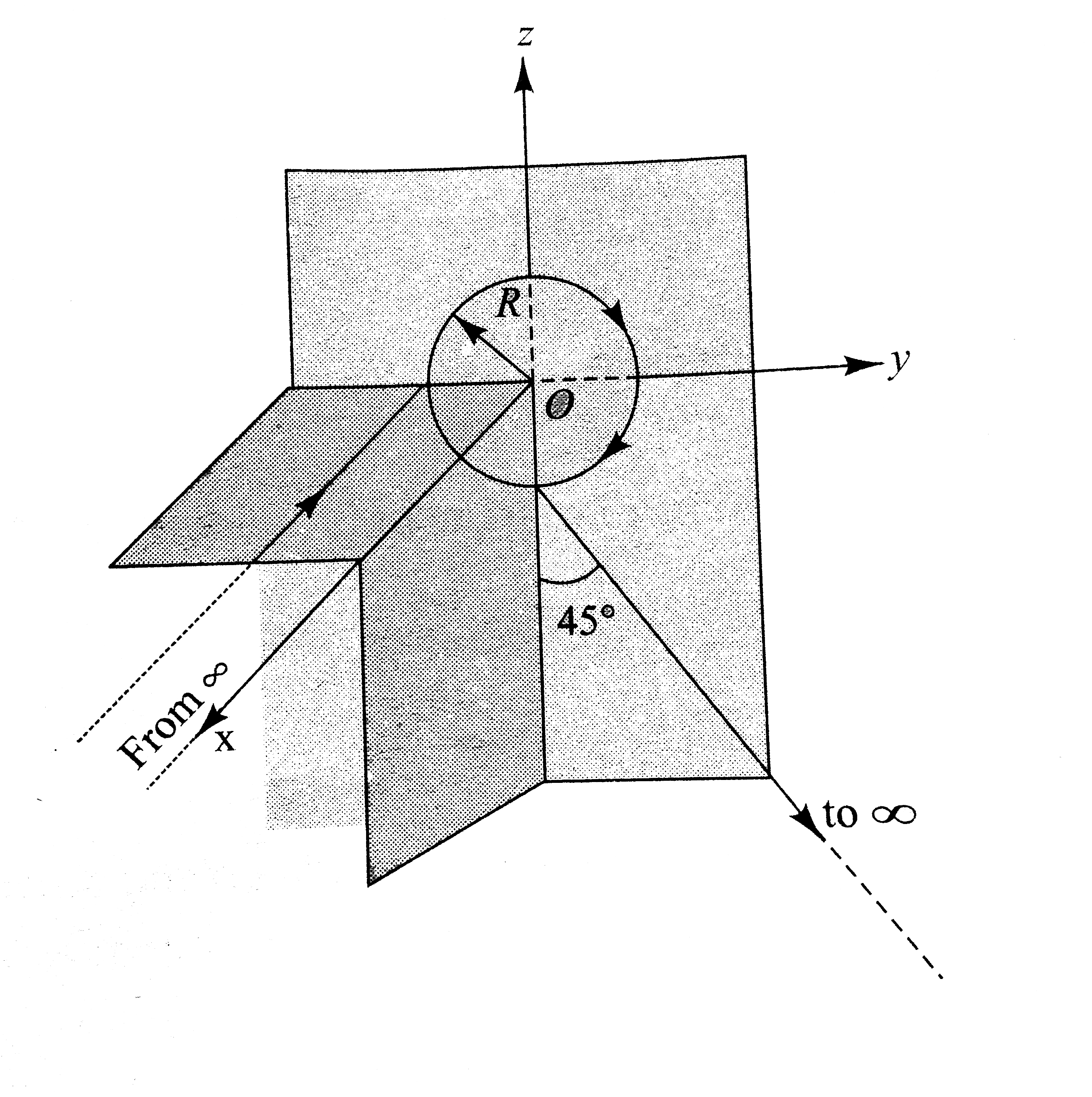
(The radius of the curved part of the wire is equal to R and linear parts of the wire are very long.)
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z-axis carries a current I in the negative z-direction. The magnetic vector field →B at a point having coordinnates (x, y) in the z = 0 plane is
View Solution
