A flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
Consider an anular ring of radius r and of thickness dr on this disc. Charge within this ring,

As ring rotates with angular velocity ω, the equivalent current is
i=(dq)(frequency)
(σ)(2πdr)(ω(2π))ori=σdrdr
=(σ)(2πdr)(ω(2π))ori=σrdr
Magnetic moment of this anulalr ring,
M=iA=(σdr)(πr2)(along the axis of rotation)
Torque on this ring
dtau=MBsin90∘=(σπr3B)dr
∴ Total torque on the disc is τ=∫R0τ(σωπB)∫R0r3dr
=σωBR44
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - Exercise160videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE1videos
MAGNETICS
- BOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery59videos
MAGNETIC FIELD AND FORCES
- BOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery1videos
MAGNETISM AND MATTER
Similar Questions
A flat insulating disc of radius 'a' carries an excess charge on its surface is of surface charge density σC/m2. Consider disc to rotate around the perpendicular to its plane with angular speed ωrad/s/ If magnetic field →B is directed perpendicular to the roation axis, then find the torque acting on the disc.
View SolutionA non-conducting thin disc of radius R charged uniformly over one side with surface density σ, rotates about its axis with an angular velocity ω. Find (a) the magnetic field induction at the centre of the disc (b) the magnetic moment of the disc.
View Solution
Knowledge Check
- Question 1 - Select One
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
AR2BR√2CR√3DR3 - Question 2 - Select One
A disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
 AzeroBωRB/πC2QωBRDnone of these
AzeroBωRB/πC2QωBRDnone of these - Question 3 - Select One
A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
A B
B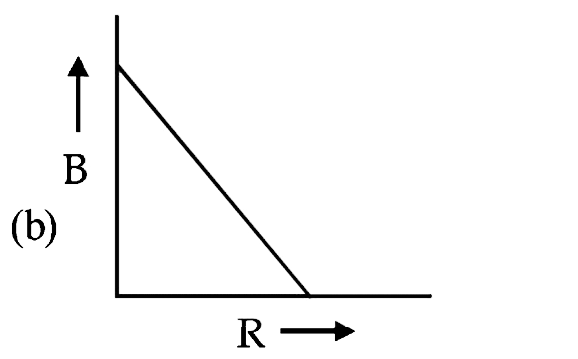 C
C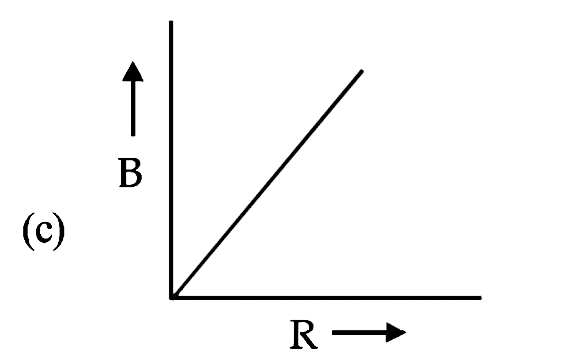 D
D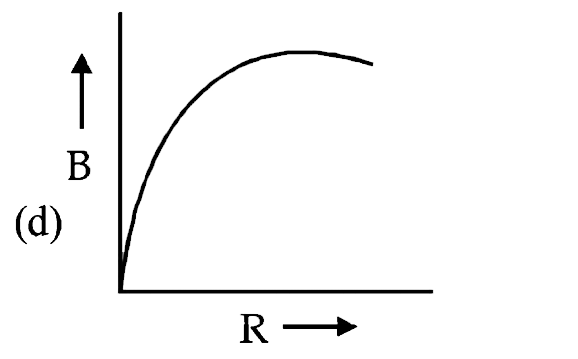
Find the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionA flat disc of radius R charged uniformly on its surface at a surface charge density σ. About its central axis of rotation it rotates at an angular speed ω. Find the magnetic moment of disc due to rotation of charges.
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionA nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity ω . The magnt moment of this disc is .
View SolutionTwo thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is :
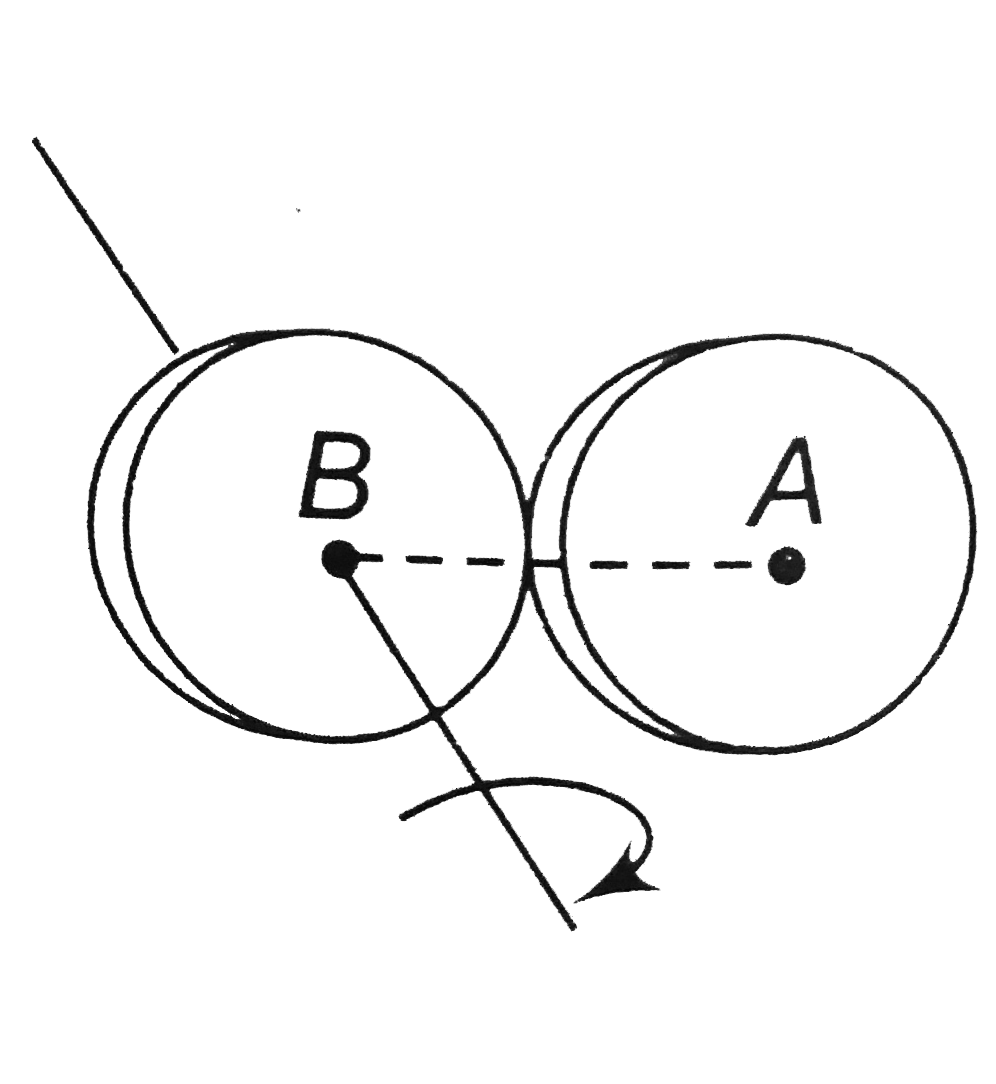 .View Solution
.View Solution

