Find the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
The correct Answer is:MR22−(M)(4R3π)2
To find the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its center of mass, we can follow these steps:
Step 1: Understand the Geometry
We have a uniform half-disc with mass M and radius R. The center of mass of the half-disc is located at a distance of 4R3π from the flat edge along the axis of symmetry.
Step 2: Moment of Inertia of a Full Disc
The moment of inertia I of a full disc about an axis perpendicular to its plane and passing through its center is given by:
Ifull=12MR2
Step 3: Moment of Inertia of the Half Disc
Since the half-disc is half of the full disc, its moment of inertia about the center (flat edge) is:
Ihalf=12Ifull=12(12MR2)=14MR2
Step 4: Apply the Parallel Axis Theorem
To find the moment of inertia about the center of mass of the half-disc, we can use the parallel axis theorem. The theorem states:
I=Icm+Md2
where d is the distance from the center of mass of the half-disc to the axis of rotation.
In our case, the distance d is 4R3π. Thus, we need to calculate:
I=Ihalf+M(4R3π)2
Step 5: Calculate the Moment of Inertia
Substituting the values we have:
I=14MR2+M(4R3π)2
Calculating (4R3π)2:
(4R3π)2=16R29π2
Thus,
I=14MR2+M⋅16R29π2
Combining the terms:
I=MR2(14+169π2)
Step 6: Final Expression
The final expression for the moment of inertia of the half-disc about the axis through its center of mass is:
I=MR2(14+169π2)
We have a uniform half-disc with mass M and radius R. The center of mass of the half-disc is located at a distance of 4R3π from the flat edge along the axis of symmetry.
The moment of inertia I of a full disc about an axis perpendicular to its plane and passing through its center is given by:
Ifull=12MR2
Since the half-disc is half of the full disc, its moment of inertia about the center (flat edge) is:
Ihalf=12Ifull=12(12MR2)=14MR2
To find the moment of inertia about the center of mass of the half-disc, we can use the parallel axis theorem. The theorem states:
I=Icm+Md2
where d is the distance from the center of mass of the half-disc to the axis of rotation.
I=Ihalf+M(4R3π)2
Substituting the values we have:
I=14MR2+M(4R3π)2
Calculating (4R3π)2:
(4R3π)2=16R29π2
Thus,
I=14MR2+M⋅16R29π2
Combining the terms:
I=MR2(14+169π2)
The final expression for the moment of inertia of the half-disc about the axis through its center of mass is:
I=MR2(14+169π2)
Topper's Solved these Questions
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 3 (Level - II)
Explore 20 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 4 (Level - I)
Explore 24 Videos
- 10 ROTATIONALBook:MOTIONChapter:10 ROTATIONALExercise:Exercise - 2 (Level - II)
Explore 25 Videos
- ALTERNATING CURRENTBook:MOTIONChapter:ALTERNATING CURRENTExercise:EXERCISE - 4 (LEVEL - II)
Explore 14 Videos
Similar Questions
State the expression for the moment of inertia of a thin uniform disc about an axis perpendicular to its plane and through its centre. Hence deduce the expression for its moment of inertia about a tangential axis perpendicular to its plane.
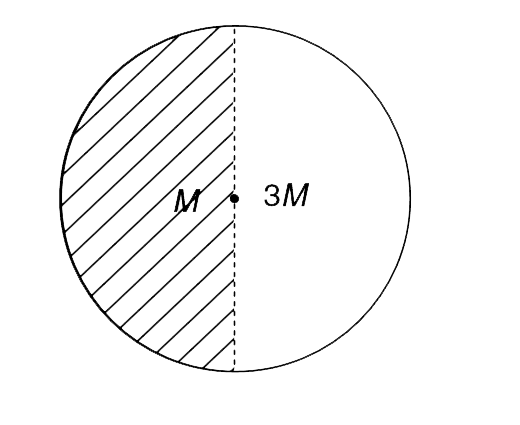
View SolutionTwo uniform semicircular discs, each of radius R, are stuck together to form a disc. Masses of the two semicircular parts are M and 3M. Find the moment of inertia of the circular disc about an axis perpendicular to its plane and passing through its centre of mass.
View Solution
Knowledge Check
The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through.
 .ABBCCDDA
.ABBCCDDAFrom a disc of radius R, a concentric circular portion of radius r is cut out so as to leave an annular disc of mass M. The moment of inertia of this annular disc about the axis perpendicular to its plane and passing through its centre of gravity is
A12M(R2+r2)B12M(R2−r2)C12M(R4+r4)D12M(R4−r4)A uniform semicircular disc of mass 'm' and radius 'R' is shown in the figure. Find out its moment of inertia about.
(a) axis 'AB'( shown in the figure 0 which passes through geometrical centre and lies in the plane of the disc
(b) axis 'CD' which passes through its centre of mass and it is perpendicular to the plane of the disc.
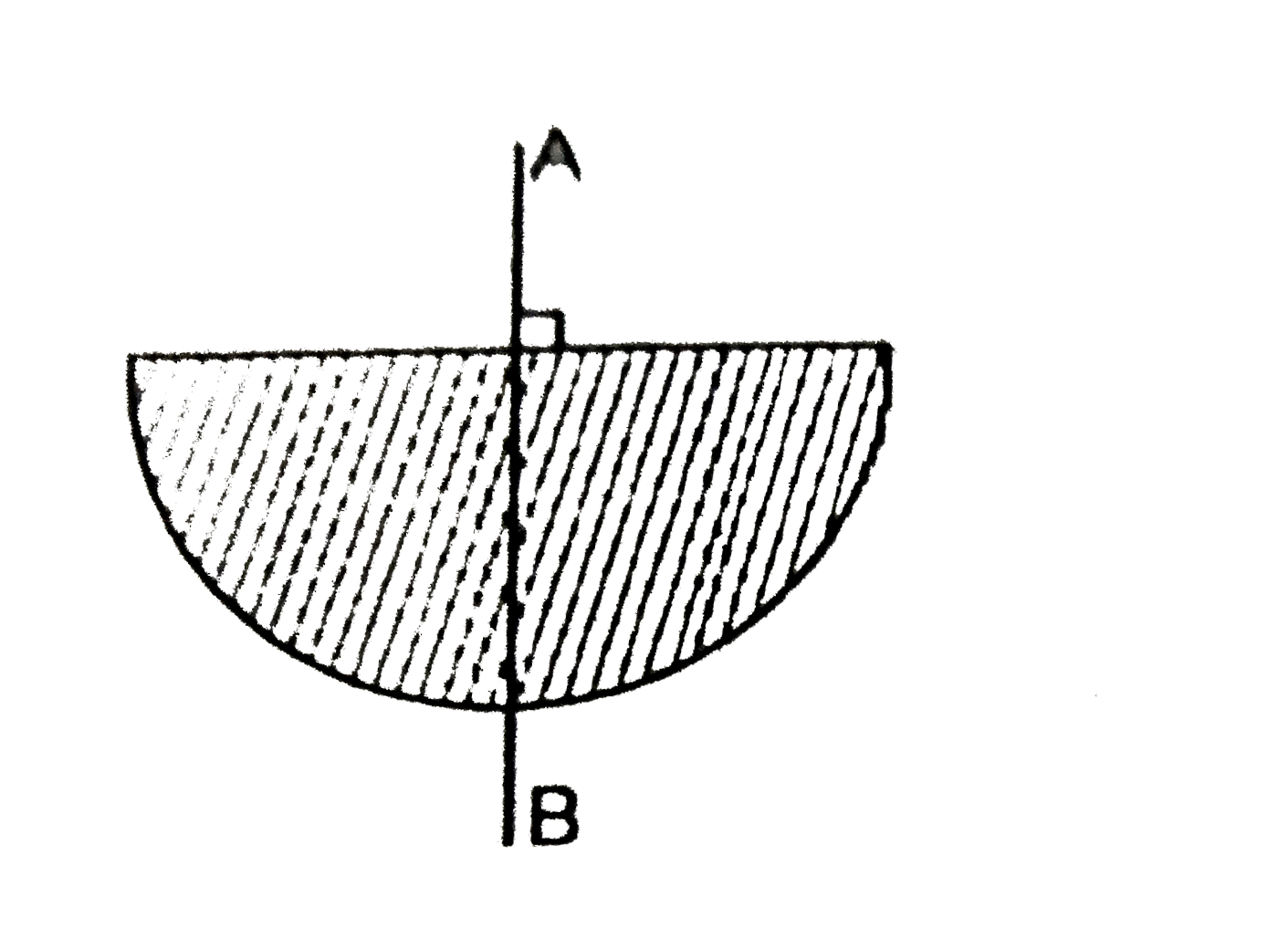 AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
AMR22−M(2Rπ)2BMR22−M(4Rπ)2CMR22+M(4R3π)2DMR22+M(2Rπ)2
Find the moment of inertia of a uniform cylinder about an axis through its centre of mass and perpendicular to its base. Mass of the cylinder is M and radius is R.
View SolutionThe mass of a thin circular plate is M and its radius is R. About an axis in the plane of plate at a perpendicular distance R/2 from centre of plate, its moment of inertia is
View SolutionThe moment of inertia of a solid sphere of radius R about an axis passing through its diameter is I. The sphere is melted and recast into a circular disc of thickness R3. The moment of inertia of this disc about an axis perpendicular to plane and passing through its centre of mass is
View SolutionRadius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
View SolutionThe moment of inertia of a uniform semicircular disc of mass disc through the centre is
View Solution