A flat uniform circular disk (radius = 2.00 m, kg) is initially stationary. The disk is free to rotate in the horizontal plane about a frictionless axis perpendic ular to the center of the disk. A 40.0-kg person, standing 1.25 m from the axis, begins to run on the disk in a circular path and has a tangential speed of relative to the ground. Find the resulting angular speed of the disk (in ) and describe the direction of the rotation.
The correct Answer is:A
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)2videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS(Linked Comprehension)3videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PROBLEMS41videos
RIGID BODY DYNAMICS-II
- BOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))3videos
RIGID BODY DYNAMICS - I
- BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)4videos
TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION
Similar Questions
x and y are the axes along the diameter of a disk of mass m and radius R. z-axis is perpendicular to plane of the disk.
Assertion: radius of gyration is same about all the axis
Reason: all axes are symmetry axes.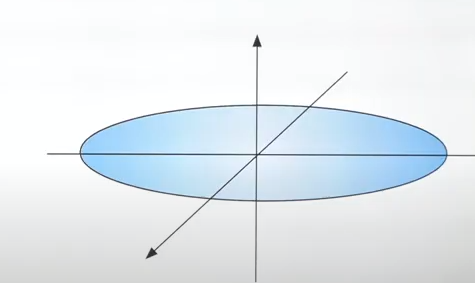 View Solution
View SolutionA disk rotstes at 70 r.p.m. in a horizontal plane. How would you place an object on the disk so that it would remain on it? The coefficient of static friction between the object and the disk is μstat=0.44.
View Solution
Knowledge Check
- Question 1 - Select One
A circular disk of radius 0.010 m rotates with a constant angular speed of 5.0 rev/s. What is the acceleration of a point on the edge of the disk?
A0.31m/s2B9.9m/s2Czero m/s2D1.6m/s2 - Question 2 - Select One
A circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
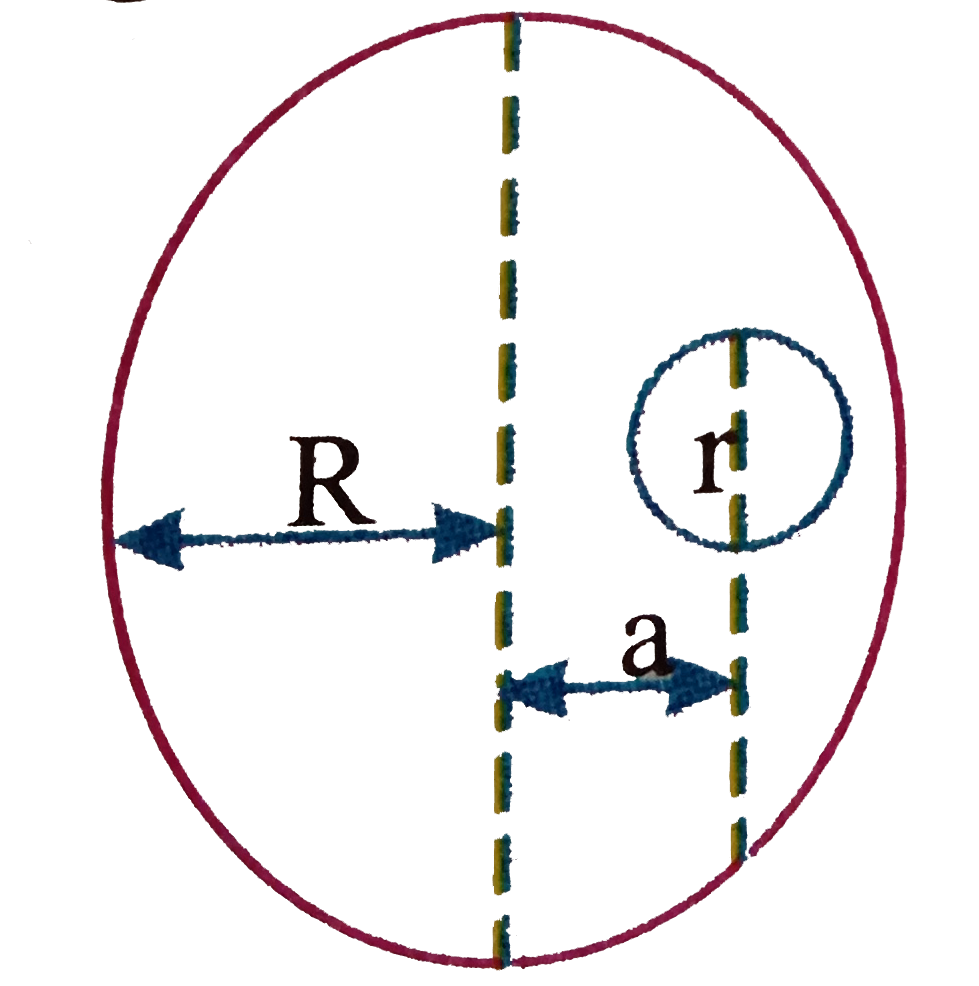 AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2
AaR2R2−r2Bar2R2−r2Ca(R2−r2)r2Da(R2−r2)R2 - Question 3 - Select One
A solid disk rotates in the horizontal plane at an angular velocity of 0.067rad/s with respect to an axis perpendicular to the disk at its center. The moment of inertia of the disk is 0.10kg.m2. From above, sand is dropped straight down onto this rotating disk, so that a thin uniform ring of sand is formed at a distance of 0.40 m from the axis. The sand in the ring has a mass of 0.50 kg. After all the sand is in place, what is the angular velocity of the disk?
A0.067rad/sB0.046rad/sC0.059rad/sD0.037rad/s
A unifrom solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .View Solution
.View SolutionA circular disk of radius 2.0 m rotates, starting from rest, with a constant angular acceleration of 20.0rad/s2. What is the tangential acceleration of a point on the edge of the disk at the instant that its angular speed is 1.0 rev/s?
View SolutionA circular disk of moment of inertia It is rotating in a horizontal plane , about its symmetry axis , with a constant angular speed ωi . Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk . Initially the second disk has zero angular speed . eventually both the disks rotate with a constant angular speed ωf . The energy lost by the initially rotating disc to friction is
View SolutionA solid circular disk has a mass of 1.2 kg and a radius of 0.16 m. Each of three identical thin rods has a mass of 0.15 kg. The rods are attached perpendicularly to the plane of the disk at its outer edge to form a three-legged stool. Find the moment of inertia of the stool with respect to an axis that is perpendicular to the plane of the disk at its center.
 View Solution
View SolutionA uniform solid disk of mass m=3.0kg and radius r=0.20m rotates about a fixed axis perpendicular to its face with angular frequency 0.6rads. The magnitude of the angular momentum of the disk when the axis of rotation momentum of the disk when the axis of rotation passes through a point midway between the centre and the rim is.
View Solution

