A small 0.500 kg object moves on a frictionless horizontal table in a circular path of radius 1.00 m. The angular speed is 6.28rad/s. The object is attached to a string of negligible mass that passes through a small hole in the table at the center of the circle. Someone under the table begins to pull the string downward to make the circle smaller. If the string will tolerate a tension of no more than 105 N, what is the radius of the smallest possible circle on which the object can move?
0.376 m
0.434 m
0.573 m
0.659 m
The correct Answer is:C
Topper's Solved these Questions
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS (More than One Option Correct Type)
2 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PRACTICE QUESTIONS(Linked Comprehension)
3 Videos
- RIGID BODY DYNAMICS-IIBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS-IIEXERCISE - PROBLEMS
41 Videos
- RIGID BODY DYNAMICS - IBOOK - RESNICK AND HALLIDAYCHAPTER - RIGID BODY DYNAMICS - IEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE))
3 Videos
- TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION BOOK - RESNICK AND HALLIDAYCHAPTER - TEMPERATURE, ZEROTH LAW OF THERMODYNAMICS AND THERMAL EXPANSION EXERCISE - PRACTICE QUETIONS (Integer Type)
4 Videos
Similar Questions
Two identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving
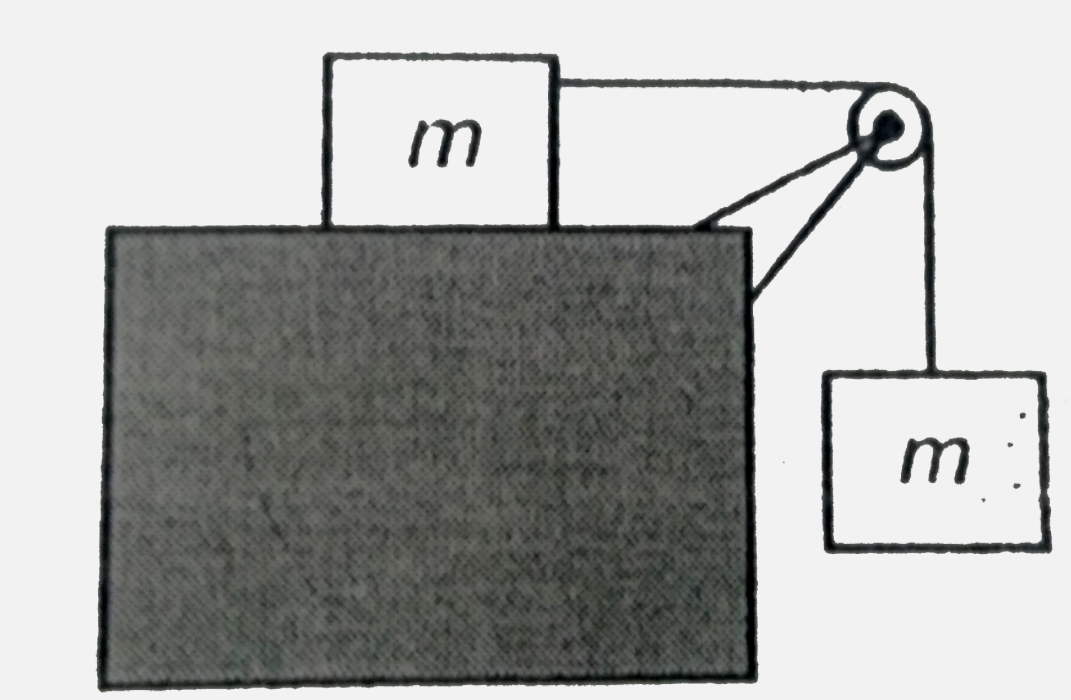
View SolutionTwo identical masses are attached by a light string that passes over a small pulley, as shown . The table and the pulley are frictionless. The hanging block is moving

View Solution
Knowledge Check
A small mass attached to a string rotates on a frictionless table top as shown in Fig. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will
 Aremain constantBincrease by a factor of 2Cincrease by a factor of 4Ddecrease by a foctor of 2
Aremain constantBincrease by a factor of 2Cincrease by a factor of 4Ddecrease by a foctor of 2A particle of mass 2 kg is on a smooth horizontal table and moves in a circular path of radius 0.6 m. The height of the table from the ground is 0.8 m. If the angular speed of the particle is 12 rad s−1 , the magnitude of its angular momentum about a point on the ground right under the centre of the circle is
A14.4kg−m2s−1B8.64kg−m2s−1C20.16kg−m2s−1D11.52kg−m2s−1A mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0. The mass is attached to a string which passes through a smooth hole in the plane as shown.
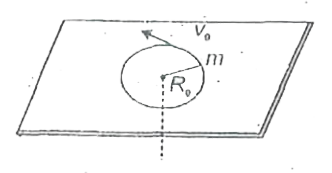
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy isA12mv20Bmv20C14mv20D2mv20
A small mass attached to a string rotates on a frictionless table top as shown. If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2, the kinetic energy of the mass will
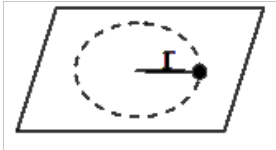
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View SolutionA particle of mass 2 kg is on a smooth horizontal table and moves in a circular path of radius 0.6 m . The height of the table from the ground is 0.8 m . If the angular speed of the particle is 12rads−1 . Find the magnitude of its angular momentum about a point on the ground right under the centre of the circle .
View SolutionA mass m moves in a circle on a smooth horizontal plane with velocity v0 at a radius R0, The mass is attached to a string which passes through a smooth hole in the plane as shown.
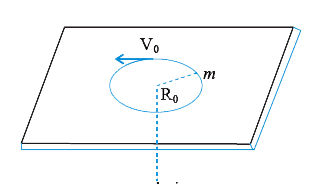
The tension in the string is increased gradually and finally m moves in a circle of radius R02. The final value of the kinetic energy is :
View Solution
