A floor-mat of mass M made up of extensible material, is rolled along its length so as to form a cylinder of radius R and kept on a rough horizontal surface. If the mat is now unrolled, without sliding, to a radius R2, the decrease in potential energy is
25MgR
57MgR
78MgR
MgR
The correct Answer is:C
To solve the problem, we need to calculate the decrease in potential energy when the mat is unrolled from a radius R to a radius R2.
1. Understanding the Initial and Final States:
- Initially, the mat is rolled into a cylinder of radius R.
- When unrolled, it forms a cylinder of radius R2.
2. Calculating the Mass Distribution:
- The mass M of the mat is uniformly distributed along its length.
- The cross-sectional area of the cylinder formed by radius R is A1=πR2.
- The cross-sectional area of the cylinder formed by radius R2 is A2=π(R2)2=πR24.
- Since the volume (and hence mass) is proportional to the cross-sectional area (assuming the length remains constant), the mass when the mat is rolled to radius R2 will be M2=M4.
3. Calculating the Heights:
- The center of mass of the cylinder when rolled to radius R is at height R.
- The center of mass of the cylinder when rolled to radius R2 is at height R2.
4. Calculating Potential Energy:
- The initial potential energy PEi when the mat is at radius R is given by:
PEi=M⋅g⋅R
- The final potential energy PEf when the mat is at radius R2 is given by:
PEf=M4⋅g⋅R2=M⋅g⋅R8
5. Calculating the Decrease in Potential Energy:
- The decrease in potential energy ΔPE is given by:
ΔPE=PEi−PEf
- Substituting the values:
ΔPE=M⋅g⋅R−M⋅g⋅R8
- Simplifying:
ΔPE=(1−18)M⋅g⋅R=78M⋅g⋅R
Final Answer:
The decrease in potential energy is 78MgR.
---
- Initially, the mat is rolled into a cylinder of radius R.
- When unrolled, it forms a cylinder of radius R2.
- The mass M of the mat is uniformly distributed along its length.
- The cross-sectional area of the cylinder formed by radius R is A1=πR2.
- The cross-sectional area of the cylinder formed by radius R2 is A2=π(R2)2=πR24.
- Since the volume (and hence mass) is proportional to the cross-sectional area (assuming the length remains constant), the mass when the mat is rolled to radius R2 will be M2=M4.
- The center of mass of the cylinder when rolled to radius R is at height R.
- The center of mass of the cylinder when rolled to radius R2 is at height R2.
- The initial potential energy PEi when the mat is at radius R is given by:
PEi=M⋅g⋅R
- The final potential energy PEf when the mat is at radius R2 is given by:
PEf=M4⋅g⋅R2=M⋅g⋅R8
- The decrease in potential energy ΔPE is given by:
ΔPE=PEi−PEf
- Substituting the values:
ΔPE=M⋅g⋅R−M⋅g⋅R8
- Simplifying:
ΔPE=(1−18)M⋅g⋅R=78M⋅g⋅R
The decrease in potential energy is 78MgR.
Topper's Solved these Questions
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - B More than One Option is Correct
26 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions
18 Videos
- WORK, POWER AND ENERGYBOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A carpet of mass M is rolled along its length so as to from a cylinder of radius R and is kept on a rough floor. When a negligibly small push is given to the cylindrical carpet, it stars unrolling itself without sliding on the floor. Calculate horizontal velocity of cylindrical part of the carpet when its radius reduces to R/2.
View SolutionA force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png)
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View SolutionA body of mass m taken form the earth's surface to the height is equal to twice the radius (R) of the earth. The change in potential energy of body will be
View SolutionA body of mass m taken form the earth's surface to the height is equal to twice the radius (R) of the earth. The change in potential energy of body will be
View SolutionA solid cylinder of mass M and radius R rolls without slipping on a flat horizontal surface. Its moment of inertia about the line of contact is
View SolutionA rectangular sheat of paper 44cm x 18cm is rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View Solution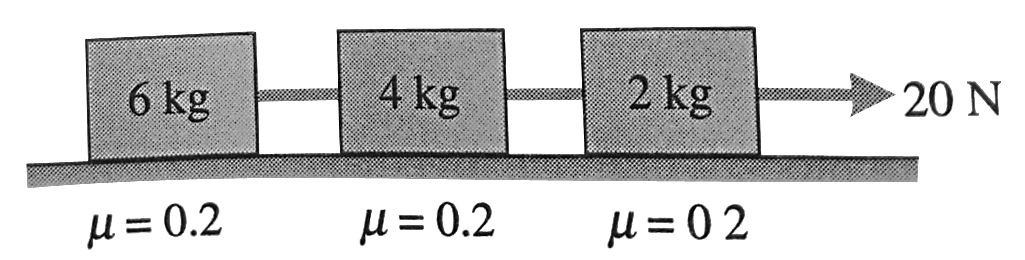
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionA rectangular sheet of paper 44cmAND18cm is a rolled along its length and a cylinder is formed. Find the radius of the cylinder.
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
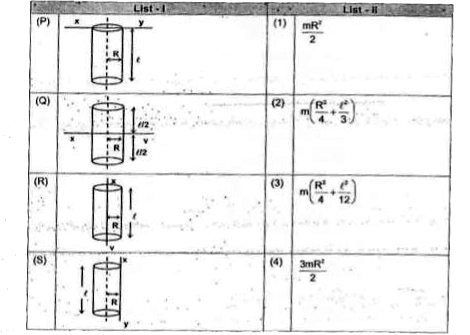
View Solution
