Match the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
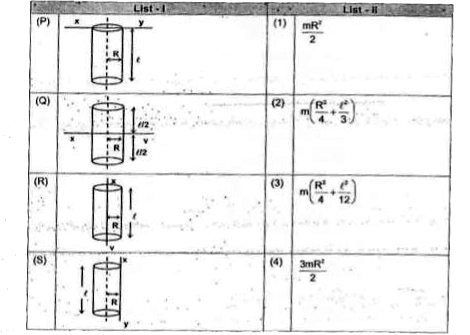
The correct Answer is:D
Step by step video & image solution for Match the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Find the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View Solution
Find the moment of inertia of a solid sphere of mass M and radius R about an axis XX shown in figure. Also find radius of gyration about the given axis.
View Solution
Find the moment of inertia of a solid sphere of mass M and radius R about an axis XX shown in figure. Also find radius of gyration about the given axis.
View SolutionWhat is moment of inertia of a cylinder of radius r, along its height?
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View SolutionThe moment of inertia of a cylinder of mass 1000gm and radius 20cm about the axis AB shown in figure is

View Solution
Find the moment of inertia of a solid sphere of mass M and radias R about an axis XX shown in figure. Also find radius of gyration about the given axis.
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionThe moment of inertia of a solid cylinder of density ρ, radius of base r, and height h about an axis passing through its centre of mass and parallel to length is
View Solution
