A force F=p+qx acts on a particle in the X - direction , where p and q are constants . If the particle is displaced from x = a to x = b , find the work done by the force .
To find the work done by the force F=p+qx on a particle as it moves from x=a to x=b, we can follow these steps:
Step 1: Understand the Work Done Formula
The work done W by a force when a particle moves from position a to position b is given by the integral of the force over the displacement:
W=∫baFdx
Step 2: Substitute the Force into the Integral
Given the force F=p+qx, we substitute this into the work done formula:
W=∫ba(p+qx)dx
Step 3: Break Down the Integral
We can split the integral into two parts:
W=∫bapdx+∫baqxdx
Step 4: Calculate Each Integral
1. The first integral:
∫bapdx=p∫ba1dx=p(x)ba=p(b−a)
2. The second integral:
∫baqxdx=q∫baxdx=q(x22)ba=q(b22−a22)=q2(b2−a2)
Step 5: Combine the Results
Now, we can combine the results of the two integrals:
W=p(b−a)+q2(b2−a2)
Step 6: Simplify the Expression
We can factor out (b−a) from the expression:
W=(b−a)(p+q2(b+a))
Final Answer
Thus, the work done by the force as the particle moves from x=a to x=b is:
W=(b−a)(p+q2(b+a))
The work done W by a force when a particle moves from position a to position b is given by the integral of the force over the displacement:
W=∫baFdx
Given the force F=p+qx, we substitute this into the work done formula:
W=∫ba(p+qx)dx
We can split the integral into two parts:
W=∫bapdx+∫baqxdx
1. The first integral:
∫bapdx=p∫ba1dx=p(x)ba=p(b−a)
∫baqxdx=q∫baxdx=q(x22)ba=q(b22−a22)=q2(b2−a2)
Now, we can combine the results of the two integrals:
W=p(b−a)+q2(b2−a2)
We can factor out (b−a) from the expression:
W=(b−a)(p+q2(b+a))
Thus, the work done by the force as the particle moves from x=a to x=b is:
W=(b−a)(p+q2(b+a))
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - PRACTICE PROBLEMS27videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WORK, ENERGY AND POWER EXERCISE - Conceptual Questions20videos
WORK, ENERGY AND POWER
- BOOK - MODERN PUBLICATIONCHAPTER - WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
WAVES
Similar Questions
A force F=a+b x acts on a particle in the X-direction, where a and b are constants. Find the work done by this force during a displacement from x=0 to x=d/
View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View Solution
Knowledge Check
- Question 1 - Select One
A force F = (2+ x)N acts on a particle in the x-direction. The work done by this force during a displacement from x = 1.0 m to x = 2.0 m is
A2.1JB2.5JC3.5JD4.5J - Question 2 - Select One
A force of (4x2+3x)N acts on a particle which displaces it from x=2m to x=3m. The work done by the force is
A32.8JB3.28JC0.328JDZero - Question 3 - Select One
A force F=(10+0.5x) acts on a particle in the x-direction. What would be the work done by this force during a displacement from x=0 to x=2m (F is in newton and x in metre)
A31.5 JB63 JC21 JD42 J
A force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA force F=(a+bx) acts on a particle in x direction where a and b are constants . Find the work done by this force during displacement from x1 to x2 .
View SolutionThe work done by a force →F during a displacement →r is given by →F.→r. Suppose a force of 12 N acts on a particle in vertically upward directionand the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionForce acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
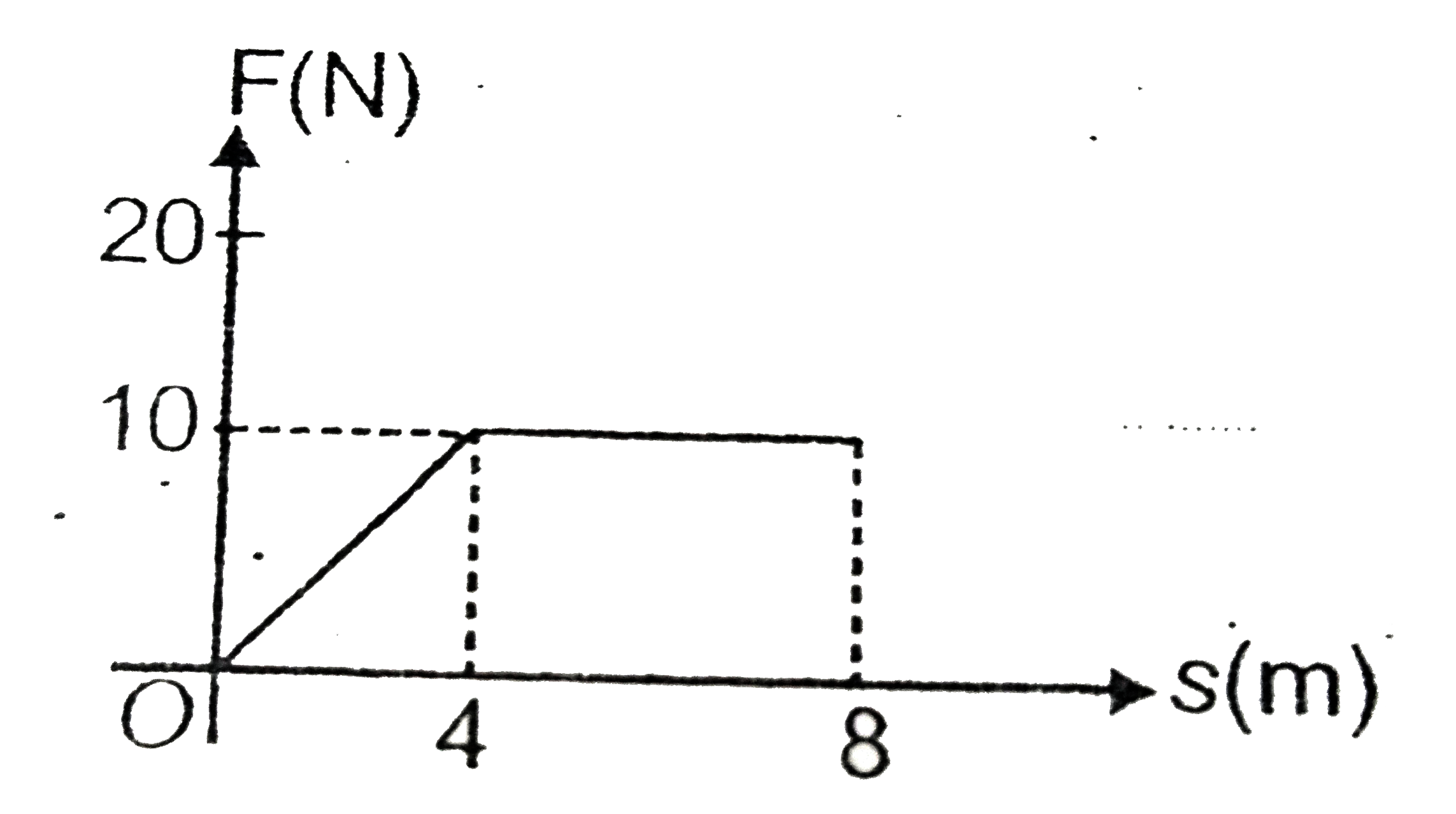 View Solution
View Solution

