The work done by a force →F during a displacement →r is given by →F.→r. Suppose a force of 12 N acts on a particle in vertically upward directionand the particle is displaced through 2.0 m in vertically downward direction. Find the work done by the force during this displacement.
The angle between the force →F and the displacement →ris1800. Thus, the work done is
W=→F.→r
=Frcosθ
=(12N)(2.0m)(cos1500
=-24N-m=-24J.
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Worked Out Examples
18 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMACHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Short Answer
14 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMACHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
Similar Questions
A force F=p+qx acts on a particle in the X - direction , where p and q are constants . If the particle is displaced from x = a to x = b , find the work done by the force .
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View Solution
Knowledge Check
A force F=(2+x) acts on a particle in x-direction where F is in newton and x in metre. Find the work done by this force during a displacement form 1. 0 m to x = 2.0 m.
A1.5JB2.5JC3.5JD4.5JWork done by a force in displacing a body is an example of
Avector productBscalar productCaddition of vectorsDdivision of vectorsWork will be said not to be done if the force and displacement are
AparallelBperpendicularCacting, in opposite directionDNone of these.
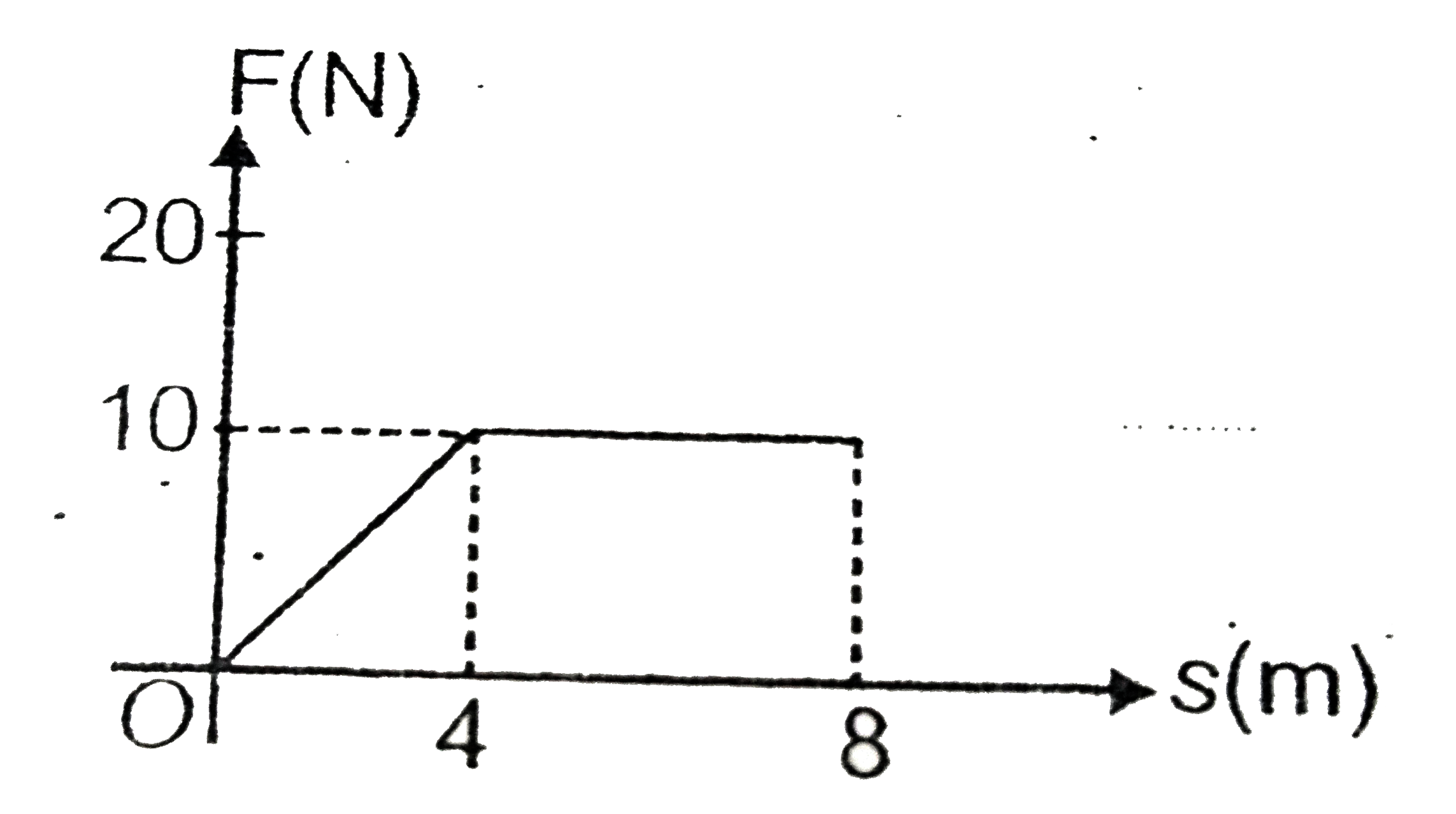
Force acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
View SolutionA force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View SolutionA force F=a+b x acts on a particle in the X-direction, where a and b are constants. Find the work done by this force during a displacement from x=0 to x=d/
View SolutionA force F=(a+bx) acts on a particle in x direction where a and b are constants . Find the work done by this force during displacement from x1 to x2 .
View Solution
