A force F=kx (where k is a positive constant) is acting on a particle Work done:
Column-1 Column-2(A)in displacing the body from x=2 to x=4(P) Negative(B)In displacing the body from x=-4 to x=-2(Q) Positive(C)In displacing the body from x=-2 to x=+2(R) Zero
The correct Answer is:(A) Q, (B) P, (C ) R
To solve the problem, we need to calculate the work done by the force F=kx during the specified displacements. The work done by a variable force can be calculated using the integral of the force over the displacement.
1. Understanding the Force:
The force acting on the particle is given by F=kx, where k is a positive constant.
2. Work Done from x=2 to x=4:
W2→4=∫42Fdx=∫42kxdx
- Integrating:
W2→4=k(x22)42=k(422−222)=k(162−42)=k(8−2)=6k
- Since k is positive, W2→4=6k is positive.
3. Work Done from x=−4 to x=−2:
W−4→−2=∫−2−4Fdx=∫−2−4kxdx
- Integrating:
W−4→−2=k(x22)−2−4=k((−2)22−(−4)22)=k(42−162)=k(2−8)=−6k
- Since k is positive, W−4→−2=−6k is negative.
4. Work Done from x=−2 to x=2:
W−2→2=∫2−2Fdx=∫2−2kxdx
- Integrating:
W−2→2=k(x22)2−2=k((2)22−(−2)22)=k(42−42)=k(2−2)=0
- Thus, W−2→2=0 is zero.
Final Answers:
- (A) Work done from x=2 to x=4 is (Q) Positive.
- (B) Work done from x=−4 to x=−2 is (P) Negative.
- (C) Work done from x=−2 to x=2 is (R) Zero.
The force acting on the particle is given by F=kx, where k is a positive constant.
W2→4=∫42Fdx=∫42kxdx
- Integrating:
W2→4=k(x22)42=k(422−222)=k(162−42)=k(8−2)=6k
- Since k is positive, W2→4=6k is positive.
W−4→−2=∫−2−4Fdx=∫−2−4kxdx
- Integrating:
W−4→−2=k(x22)−2−4=k((−2)22−(−4)22)=k(42−162)=k(2−8)=−6k
- Since k is positive, W−4→−2=−6k is negative.
W−2→2=∫2−2Fdx=∫2−2kxdx
- Integrating:
W−2→2=k(x22)2−2=k((2)22−(−2)22)=k(42−42)=k(2−2)=0
- Thus, W−2→2=0 is zero.
- (A) Work done from x=2 to x=4 is (Q) Positive.
- (B) Work done from x=−4 to x=−2 is (P) Negative.
- (C) Work done from x=−2 to x=2 is (R) Zero.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions11videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, POWER AND ENERGYEXERCISE - C Comprehension Type Questions18videos
WORK, POWER AND ENERGY
- BOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY33videos
WORK, ENERGY AND POWER
Similar Questions
A force of →F=2xˆi+2ˆj+3z2ˆkN is acting on a particle. Find the work done by this force in displacing the body from (1,2,3)m to (3,6,1)m.
View SolutionThe relationship between force and position is shown in fig ( in one dimensional case). The work done in displacing a body from x=1cm to x = 5 cm is:
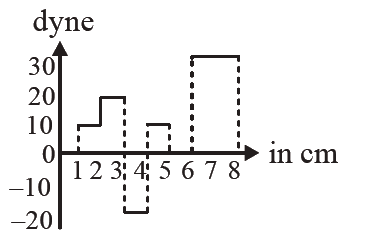 View Solution
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionThe work done by a force →F=(−6x2ˆi)N in displacing a particle from x = 4mtox = -2mis
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=+2a. Where, k is a positive constant.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
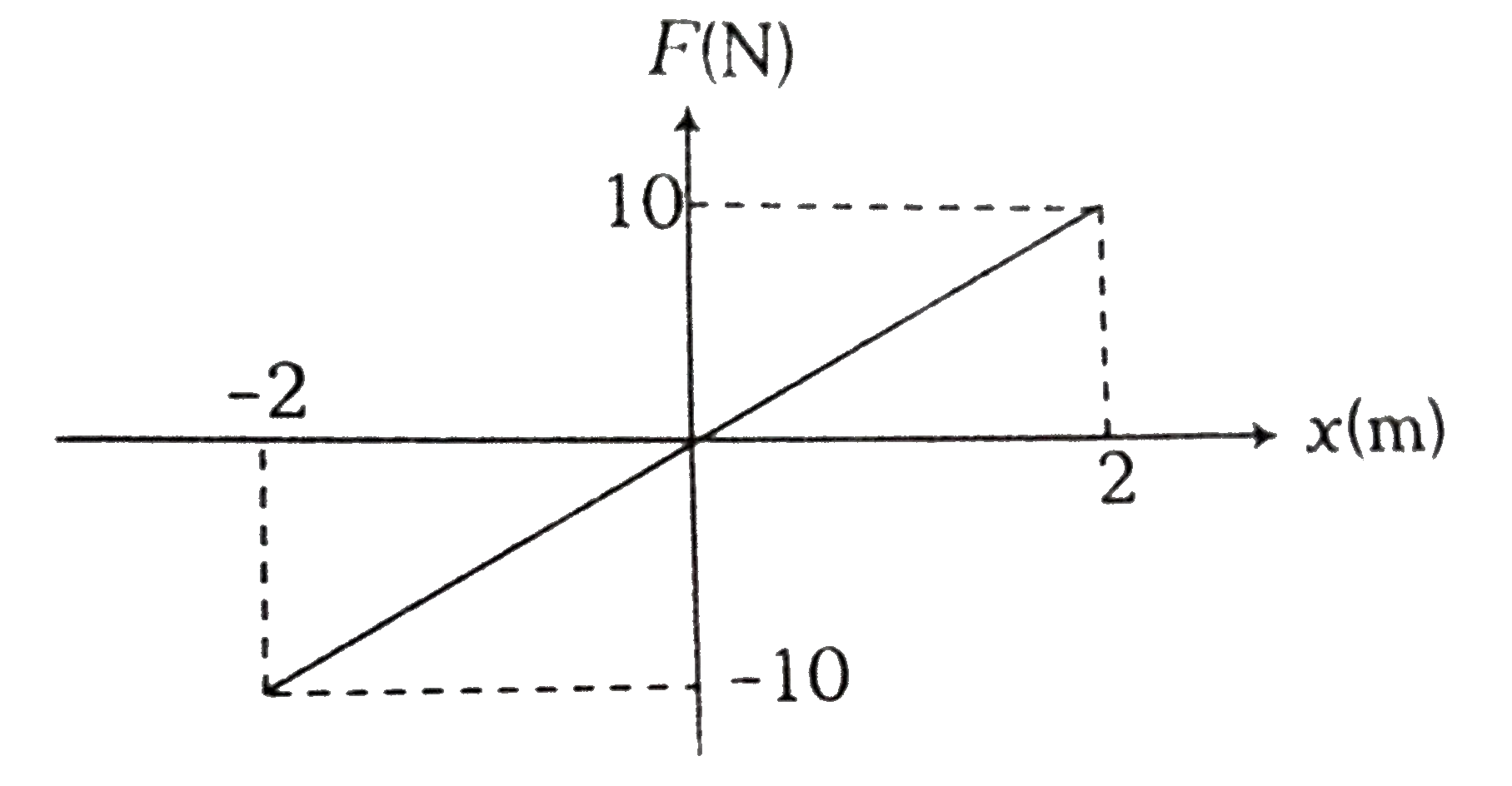 View Solution
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in Newtown and x is in meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=a+bx acts on a particle in the x-directioin, where a and b are constants. Find the work done by this force during a displacement form x=0→x=d.
View Solution

