A force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
To solve the problem, we need to calculate the work done by the force acting on the block. Here are the steps to arrive at the solution:
Step 1: Identify the Given Values
- Force (F) = 10 N
- Mass of the block (m) = 20 kg
- Coefficient of friction (μ) = 0.2
- Gravitational acceleration (g) = 10 m/s² (assuming standard value)
Step 2: Calculate the Weight of the Block
The weight (W) of the block can be calculated using the formula:
W=m⋅g
W=20kg⋅10m/s2=200N
Step 3: Calculate the Normal Force
Since the block is on a horizontal surface, the normal force (N) is equal to the weight of the block:
N=W=200N
Step 4: Calculate the Maximum Frictional Force
The maximum static frictional force (F_friction) can be calculated using the formula:
Ffriction=μ⋅N
Ffriction=0.2⋅200N=40N
Step 5: Compare Applied Force and Frictional Force
The applied force (10 N) is less than the maximum static frictional force (40 N). This means that the block will not move because the frictional force is sufficient to counteract the applied force.
Step 6: Calculate the Displacement
Since the block does not move, the displacement (d) is:
d=0m
Step 7: Calculate the Work Done by the Force
Work done (W) is calculated using the formula:
W=F⋅d
Since the displacement is zero:
W=10N⋅0m=0J
Final Answer
The work done by the force is 0 Joules.
---
- Force (F) = 10 N
- Mass of the block (m) = 20 kg
- Coefficient of friction (μ) = 0.2
- Gravitational acceleration (g) = 10 m/s² (assuming standard value)
The weight (W) of the block can be calculated using the formula:
W=m⋅g
W=20kg⋅10m/s2=200N
Since the block is on a horizontal surface, the normal force (N) is equal to the weight of the block:
N=W=200N
The maximum static frictional force (F_friction) can be calculated using the formula:
Ffriction=μ⋅N
Ffriction=0.2⋅200N=40N
The applied force (10 N) is less than the maximum static frictional force (40 N). This means that the block will not move because the frictional force is sufficient to counteract the applied force.
Since the block does not move, the displacement (d) is:
d=0m
Work done (W) is calculated using the formula:
W=F⋅d
Since the displacement is zero:
W=10N⋅0m=0J
The work done by the force is 0 Joules.
Topper's Solved these Questions
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Solved Examples
15 Videos
- WORK, POWER & ENERGYBOOK - CENGAGE PHYSICSCHAPTER - WORK, POWER & ENERGYEXERCISE - Exercise 8.1
25 Videos
- VECTORSBOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A force F is acting at an angle θ with horizontal on a block of mass 12 kg placed on a rough 3 horizontal surface having coefficient of friction μ=34 as shown in the figure. The minimum value of force F to just move the block will be (g=10ms−2)
View SolutionA horizontal force of 129.4 N is applied on a 10 kg block which rests on a horizontal surface. If the coefficient of friction is 0.3, the acceleration should be
View Solution
Knowledge Check
A block of mass 2 kg initially at rest moves under the action of an applied horizontal force of 6 N on a rough horizontal surface. The coefficient of friction between block and surface is 0.1. The work done by the applied force in 10 s is (Take g=10ms−2)
A200JB−200JC600 JD−600JA 100 N force acts horizontally on a block of 10 kg placed on a horizontal rough surface of coefficient of friction μ=0.5. If the acceleration due to gravity (g) is taken as 10ms−2, the acceleration of the block (in ms−2) is
A2.5B10C5D7.5A force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
A12B14C16D18
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
View SolutionA force of 100N is applied on a block of mass 3kg as shown in the figure. The coefficient of friction between the surface and the block is μ=1√3 . The friction force acting on the bock is.
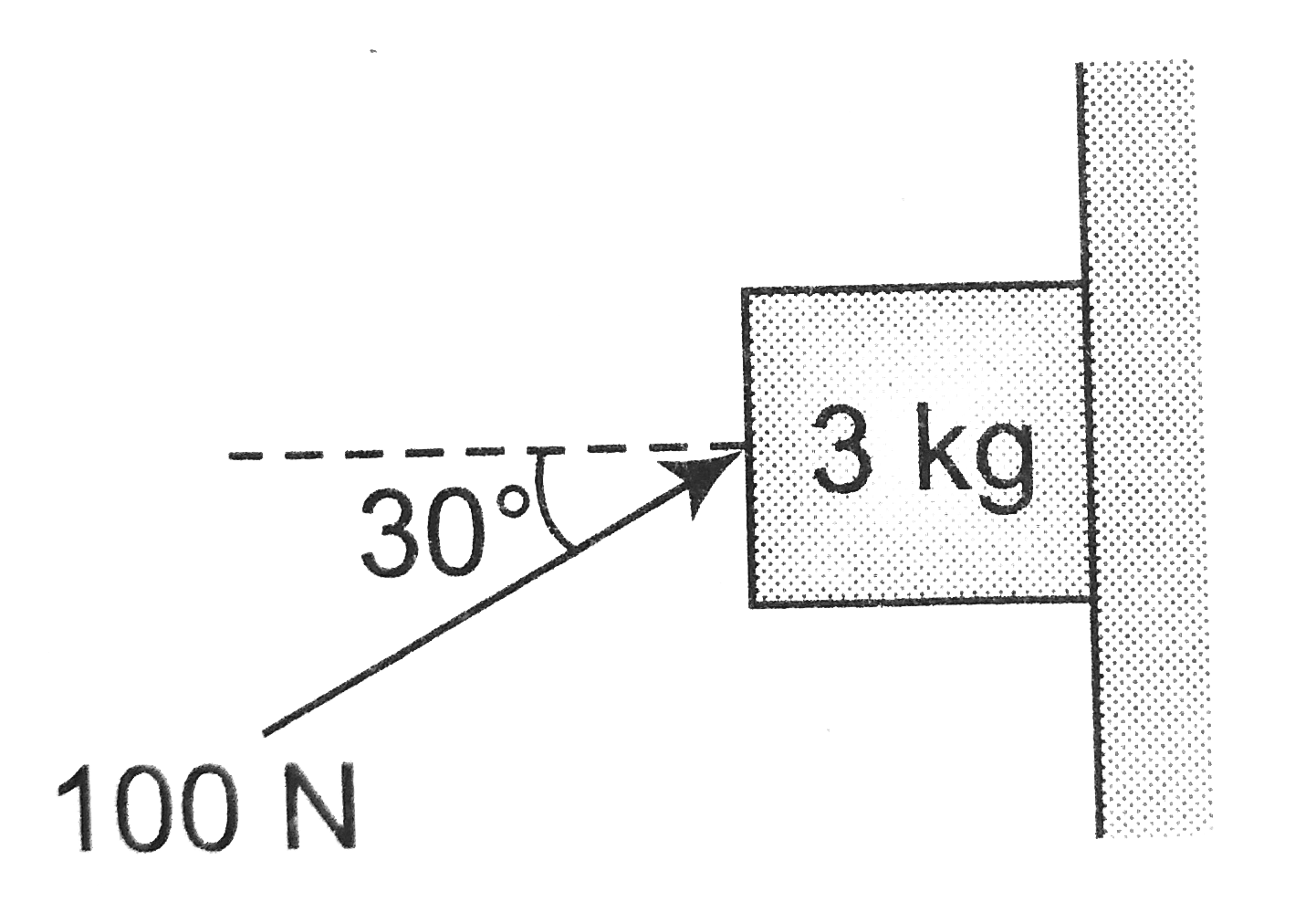
View SolutionA rectangular block of mass 5 kg is kept on a horizontal surface . The coefficient of friction between the block and the surface is 0.2 . If a force of 20 N is applied to the block at angle of 30∘ with the horizontal plane , what is the force of friction on the block ? (Take g = 10m/s2)
View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View Solution
In the figure shown, a block of weight 10 N resting on a horizontal surface. The coefficent of static friction between the block and the surface μs=0.4 . A force of 3.5 N will keep the block in uniform motion, once it has been set in motion. A horizontal force force of 3N is applid to the block, then the block will
View Solution