A force F is acting at an angle with horizontal on a block of mass 12 kg placed on a rough 3 horizontal surface having coefficient of friction as shown in the figure. The minimum value of force F to just move the block will be
36N
96N
72N
54N
To find the minimum value of the force F required to just move the block, we can follow these steps:
Step 1: Identify the forces acting on the block
The forces acting on the block include:
- The weight of the block mg acting downwards.
- The normal force N acting upwards.
- The applied force F at an angle θ with horizontal, which can be resolved into two components:
- Horizontal component: Fcosθ
- Vertical component: Fsinθ
- The frictional force f acting opposite to the direction of motion.
Step 2: Write the equations for vertical forces
In the vertical direction, the forces must balance out:
N+Fsinθ=mg
From this, we can express the normal force N:
N=mg−Fsinθ
Step 3: Write the equation for maximum frictional force
The maximum frictional force fmax is given by:
fmax=μN
Substituting for N:
fmax=μ(mg−Fsinθ)
Step 4: Set up the equation for motion
For the block to just start moving, the horizontal component of the applied force must equal the maximum frictional force:
Fcosθ=μ(mg−Fsinθ)
Step 5: Rearranging the equation
Rearranging the equation gives:
Fcosθ+μFsinθ=μmg
Factoring out F:
F(cosθ+μsinθ)=μmg
Thus, we can express F:
F=μmgcosθ+μsinθ
Step 6: Substitute values and find F
Given:
- m=12kg
- g=10m/s2
- μ=34
Substituting these values into the equation:
F=34×12×10cosθ+34sinθ
F=90cosθ+34sinθ
Step 7: Minimize the denominator
To find the minimum value of F, we need to minimize the denominator cosθ+34sinθ.
Step 8: Differentiate and find critical points
Differentiating with respect to θ and setting the derivative to zero:
−sinθ+34cosθ=0
This gives:
tanθ=34
Step 9: Calculate cosθ and sinθ
Using the triangle relationships:
sinθ=35,cosθ=45
Step 10: Substitute back to find F
Substituting cosθ and sinθ back into the equation for F:
F=9045+34⋅35
Calculating the denominator:
=9045+920=901620+920=902520=90×2025=72N
Final Answer
The minimum value of the force F required to just move the block is 72N.
---
The forces acting on the block include:
- The weight of the block mg acting downwards.
- The normal force N acting upwards.
- The applied force F at an angle θ with horizontal, which can be resolved into two components:
- Horizontal component: Fcosθ
- Vertical component: Fsinθ
- The frictional force f acting opposite to the direction of motion.
In the vertical direction, the forces must balance out:
N+Fsinθ=mg
From this, we can express the normal force N:
N=mg−Fsinθ
The maximum frictional force fmax is given by:
fmax=μN
Substituting for N:
fmax=μ(mg−Fsinθ)
For the block to just start moving, the horizontal component of the applied force must equal the maximum frictional force:
Fcosθ=μ(mg−Fsinθ)
Rearranging the equation gives:
Fcosθ+μFsinθ=μmg
Factoring out F:
F(cosθ+μsinθ)=μmg
Thus, we can express F:
F=μmgcosθ+μsinθ
Given:
- m=12kg
- g=10m/s2
- μ=34
F=34×12×10cosθ+34sinθ
F=90cosθ+34sinθ
To find the minimum value of F, we need to minimize the denominator cosθ+34sinθ.
Differentiating with respect to θ and setting the derivative to zero:
−sinθ+34cosθ=0
This gives:
tanθ=34
Using the triangle relationships:
sinθ=35,cosθ=45
Substituting cosθ and sinθ back into the equation for F:
F=9045+34⋅35
Calculating the denominator:
=9045+920=901620+920=902520=90×2025=72N
The minimum value of the force F required to just move the block is 72N.
Similar Questions
A force F is applied on a block of mass √3kg which rests on a horizontal surface with a coefficient of friction 12√3. The maximum value of F for which the block doesn't move, is [Take g=10ms−2]
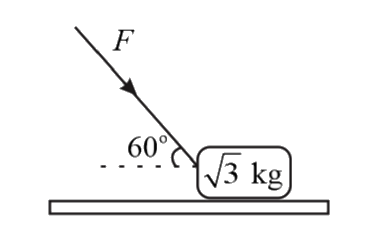
View SolutionA force of 10N is acting on a block of 20kg on horizontal surface with coefficient of friction μ=0.2. Calculate the work done by the force.
View Solution
Knowledge Check
A block of mass 10kg is placed on a rough horizontal surface having coefficient of friction μ=0.5 . If a horizontal force of 100N is acting on it, then acceleration of the will be.
A0.5m/s2B5m/s2C10m/s2D15m/s2A block of mass 2 kg is kept on a rough horizontal floor an pulled with a force F. If the coefficient of friction is 0.5. then the minimum force required to move the block is :-
 A10 NB10011NC1008ND20 N
A10 NB10011NC1008ND20 NA force of 49 N just able to move a block of wood weighing 10 kg on a rough horizontal surface , then coefficient of friction is
A12B14C16D18
What is the value of applied force ‘F’ which is exerted at an angle θ with the horizontal on a block of mass ‘m’ placed on a horizontal rough surface, if the coefficient of static friction between the block and the surface is , such that the block is on the verge of moving horizontally?
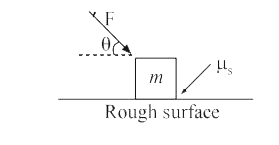
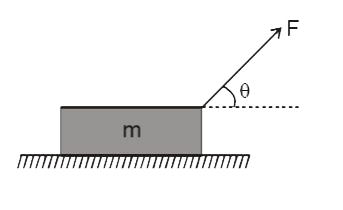
View SolutionA wooden block of mass m resting on a rough horizontal table (coefficient of friction =μ ) is pulled by a force F as shown in figure.The acceleration of the block moving horizontally is:
View SolutionA block is placed on a rough horizontal surface having coefficient of friction mu. A variable force F=kt,(0<t<mgksinθ acts on it at an angle θ to

View SolutionA force F is applied on a block of mass √3kg which rests on a horizontal surface with a coefficient of friction 12√3. The maximum value of F for which the block doesn't move, is [Take g=10ms−2]

View SolutionA block of mass m=5kg is resting on a rough horizontal surface for which the coefficient of friction is 0.2 . When a force F=40N is applied, the acceleration of the block will be (g=10m/s2) .

View Solution
