A force of 9 N pulls a block of 4 kg through a rope of mass 0.5 kg. The block is resting on a smooth surface. What is the force of reaction exerted by the block on the rope?
The correct Answer is:8 N
To solve the problem step by step, we will analyze the forces acting on both the block and the rope, and then use Newton's second law to find the force of reaction exerted by the block on the rope.
Step 1: Identify the Forces Acting on the Rope
- The rope has a mass of 0.5 kg and is being pulled by a force of 9 N.
- The normal reaction force (N) exerted by the block on the rope acts upwards on the rope.
- The net force acting on the rope can be expressed as:
Fnet, rope=9N−N
Step 2: Apply Newton's Second Law to the Rope
- According to Newton's second law, the net force is equal to the mass of the rope multiplied by its acceleration (A):
Fnet, rope=mrope⋅A
- Substituting the values, we have:
9−N=0.5⋅A
- Rearranging gives us:
A=9−N0.5
Step 3: Identify the Forces Acting on the Block
- The block has a mass of 4 kg and experiences the normal force (N) from the rope.
- The acceleration of the block is also A since both the block and rope are moving together.
Step 4: Apply Newton's Second Law to the Block
- For the block, the equation can be expressed as:
N=mblock⋅A
- Substituting the mass of the block:
N=4⋅A
Step 5: Substitute the Expression for A into the Block's Equation
- From the equation for A derived from the rope, substitute into the block's equation:
N=4⋅(9−N0.5)
- Simplifying gives:
N=4⋅(18−2N)
N=72−8N
N+8N=72
9N=72
N=729=8N
Step 6: Conclusion
- The force of reaction exerted by the block on the rope is 8 N.
- The rope has a mass of 0.5 kg and is being pulled by a force of 9 N.
- The normal reaction force (N) exerted by the block on the rope acts upwards on the rope.
- The net force acting on the rope can be expressed as:
Fnet, rope=9N−N
- According to Newton's second law, the net force is equal to the mass of the rope multiplied by its acceleration (A):
Fnet, rope=mrope⋅A
- Substituting the values, we have:
9−N=0.5⋅A
- Rearranging gives us:
A=9−N0.5
- The block has a mass of 4 kg and experiences the normal force (N) from the rope.
- The acceleration of the block is also A since both the block and rope are moving together.
- For the block, the equation can be expressed as:
N=mblock⋅A
- Substituting the mass of the block:
N=4⋅A
- From the equation for A derived from the rope, substitute into the block's equation:
N=4⋅(9−N0.5)
- Simplifying gives:
N=4⋅(18−2N)
N=72−8N
N+8N=72
9N=72
N=729=8N
- The force of reaction exerted by the block on the rope is 8 N.
Topper's Solved these Questions
Similar Questions
A rope of mass 0.5kg is pulling a block of mass 10kg under the action of force of 31.5N If the block is resting on a smooth horizontal surface calculate the force of reaction exerted by the block on the rope .
View SolutionA pull of 15 N is applied to a rope attached to a block of mass 7 kg lying on a smooth horizontal surface. The mass of the rope is 0.5 kg. What is the force exerted by the block on the rope?
View Solution
Knowledge Check
A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
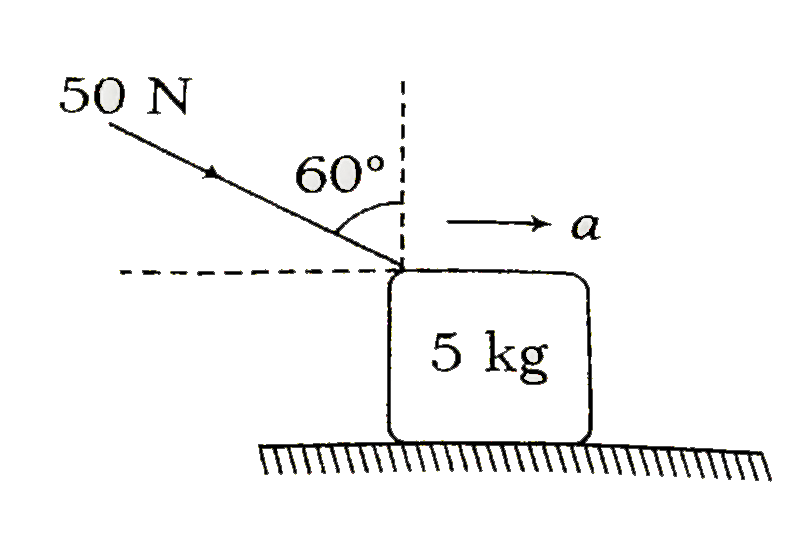 A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2A block of mass 1 kg is placed on a horizontal surface . The reaction force to the weight of the block is
AThe 10 N normal force from the surfaceBThe 10 N reaction force from the block of the surfaceCThe weight of the earthDA 10 N force on earthA block of mass 3kg is at rest on a rough inclined plane as shown in the figure. The magnitude of net force exerted by the surface on the block will be
 A26NB19.5NC10ND30N
A26NB19.5NC10ND30N
A force of 50 N acts in the direction as shown in figure. The block of mass 5kg. Resting on a smooth horizonatal surface. Find out the acceleration of the block.
View SolutionA horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View Solution
A block of mass 2 m is pulled along a horizontal frictionless surface by a rope of mass m as shown in the figure given above. What force is exerted by the rope on the block ?
View SolutionA horizontal force of 20 N is applied to a block of 10 kg resting on a rough horizontal surface. How much additional force is required to just move the block, if the coefficient of static friction between the block and the surface is 0.4 ?
View SolutionTwo forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
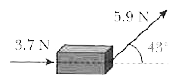
View Solution
