A force newton acts in a region where a particle moves annticlockwise in a square loop of 2m in xy plane as shown in figure . Calculate the total amount of work done. Is this force a conservative force or a non-conservative force?
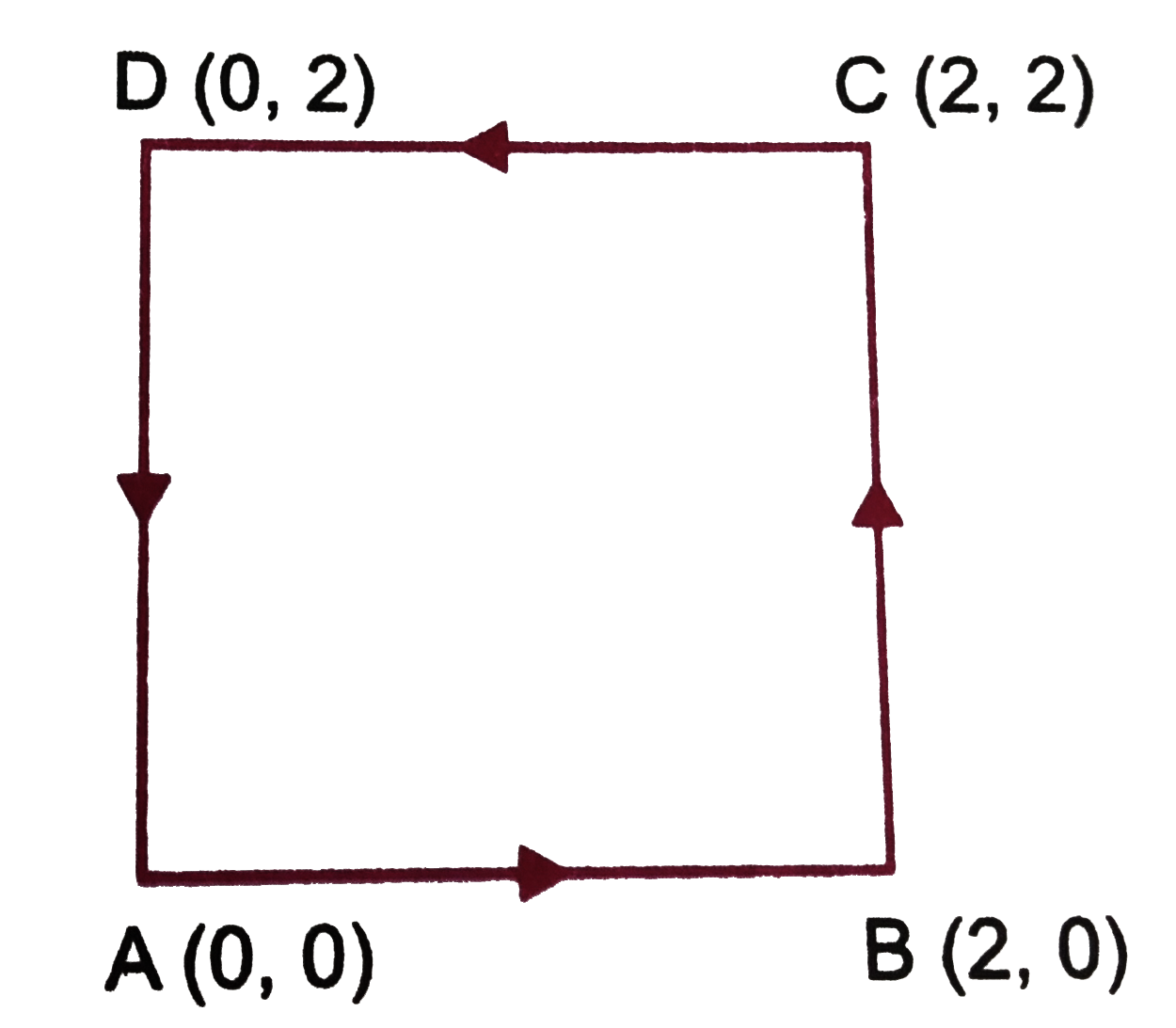
Here, newton
Total work done in moving the particle
As work done by the force around a round trip is not zero, therefore, the force must be non-conservative.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Conceptual Problems
27 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.
54 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Curiosity questions
2 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Knowledge Check
Assertion : Work is done only by conservative force.
Reason : Non conservative forces are no good to do any work.AIf both, Assertion and Reason are true and Reason is correct explantion of Assertion.BIf both, Assertion and Reason are true but Reason is not a correct explanation of the Assertion.CIf Assertion is true but the Reason is false.DIf both, Assertion and Reason are false.
Is work done by a non conservative force always negative ? Comment.
View SolutionForce acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionForce acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
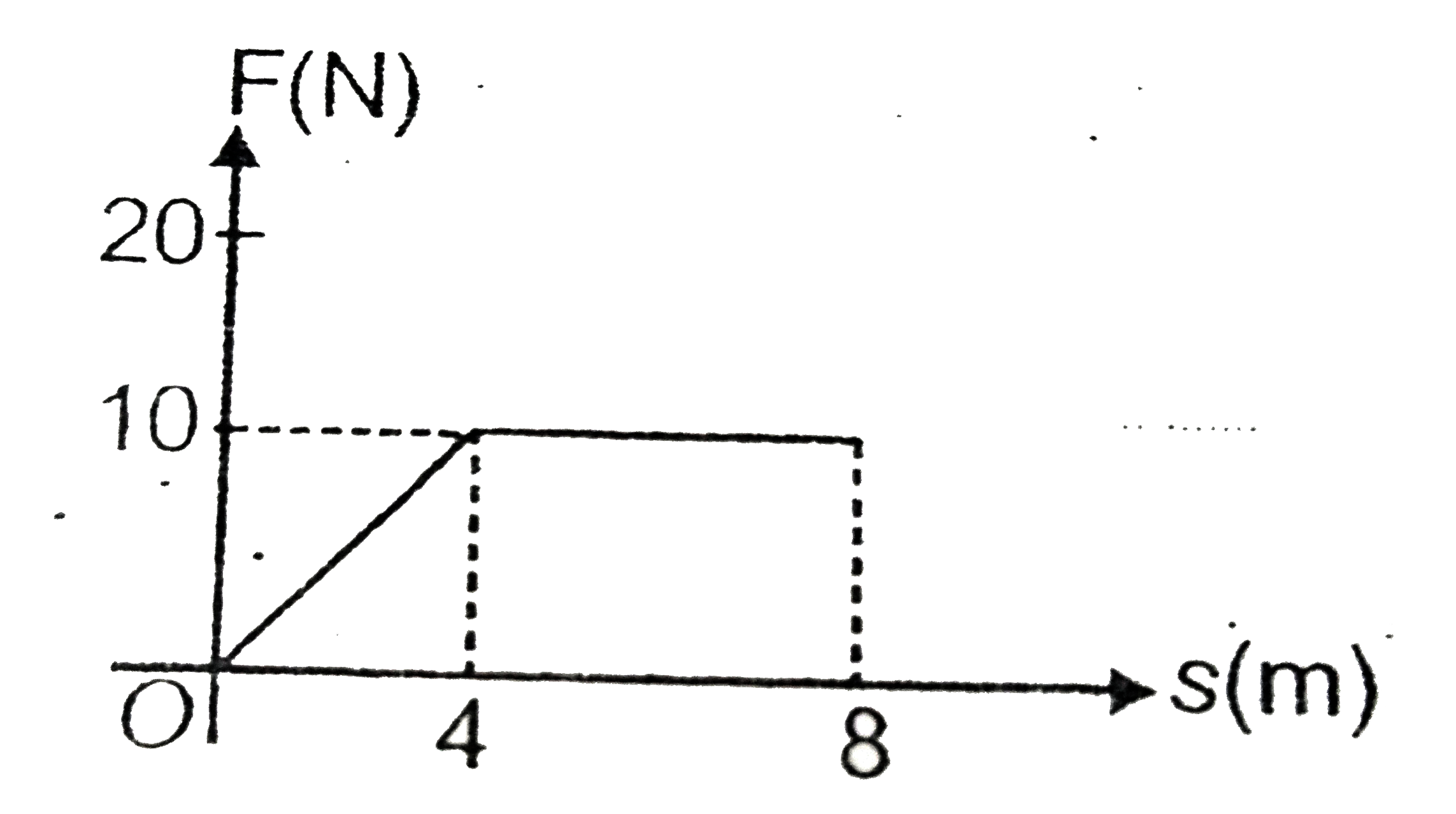
View SolutionWork done by various forces, Potential and kinetic energy. Conservative and non conservative forces
View SolutionA force →F=(−yˆi+xˆj)N acts on a particle as it undergoes counterclockwise circular motion in x-y plane in a circle of radius 4 m and with the centre at origin. If the work done by the force when the particle undergoes one complete revolution is (assume x,y are in m) 4πλ joule then calculation λ.
View SolutionA force →F=xˆi+y2ˆjN acts on a particle and the particle moves from (1,2)m to (–3,4)m. Find work done by the force →F.
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View Solution
