A frog sits on the end of a long board of length L=5m. The board rests on a frictionless horizontal table. The frog wants to jump to the opposite end of the board. What is the minimum take-off speed (in m/s), i.e., relative to ground 'v' that allows the frog to do the trick? The board and the frog have equal masses.
2√5ms−1
5ms−1
5√2ms−1
10√2ms−1
The correct Answer is:C
Let the speed of the board be u and from jumps with angle of inclination to the board θ, then from conservation of momentum in horizontal direction.
mvcosθ−μ=0
u=vcosθ..........(i)
Let distance moved by board be x
So, L−x=ut......................(ii) and x=vcosθt....................(iii)
Solving above equation, we get
Also, x=v2sing2θg
⇒(L2)=v2sin2θg ⇒v = √gL2sin2θ
Hence, v should be minimum for sin2θ=1(i.e., maximum)
⇒vmin= (√gL2=√10×102=√50=5√2ms9−1)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Match the coloumns
9 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A frog sits on the end pf a long boord of length L. the boord rests on a fricationless horizontal table. The frog wants os the minimum takes - off speed i.e relative to ground v that allows the frog yo do the trick? The board and the frog have equal masses.
View SolutionA 50kg man is standing at one end of a 3m long plank of mass 100kg. The plank is sliding towards the right with uniform velocity of 2 m / s on the frictionless horizontal ground. The man walks to the other end of the plank in 5s. Find the distance travelled (in m ) by the man'relative to the ground in this 5 s interval.
'(##CEN_KSR_PHY_JEE_C08_E01_033_Q22##)'
View Solution
Knowledge Check
A man of mass m moves with a constant speed on a plank of mass 'M' and length 'L' kept initially at rest on a frictionless horizontal surface, from one end to the other in time 't'. The speed of the plank relative to ground while man is moving, is -
ALt(Mm)BLt(mM+m)CLt(mM−m)DNone of theseA man of mass m moves with a constant speed on a plank of mass M and length l kept initially at rest on a frictionless horizontal surface, from one end to the other in time t. The speed of the plank relative to grounud while man is moving, is
Alt(Mm)Blt(mm+M)Clt(MM+m)DNone of theseOne end of an ideal spring of unstreched length lO=1m, is fixed on a frictionless horizontal table. The other end has a small disc of mass 0.1kg attached to it. The disc is projected with a velocity υ0=11m/s perpendicular to the spring.

What is the force constant of spring?A210N/mB100N/mC110N/mD200N/m
Two small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.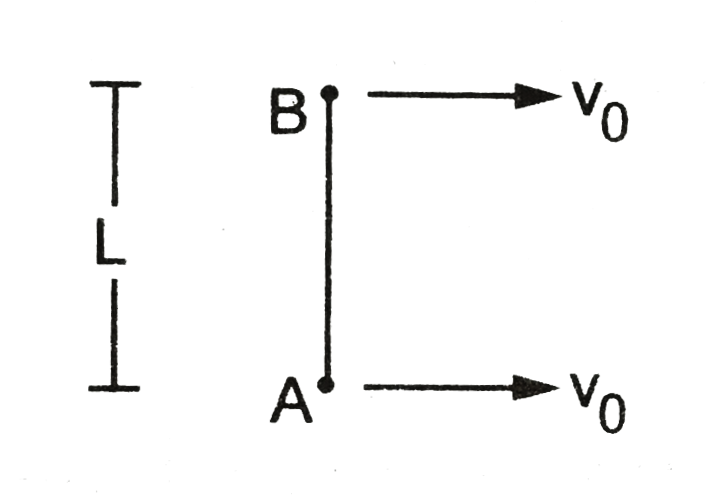
View SolutionOne end of a string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lower most point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionA boy of mass 25 kg stands on a board of maas 10 kg which in turn is kept on a frictionless horizontal ice surface. The boy maks a jump with a velocity component 5m/s in a horizontal direction with respect to the ice. With what velocity does the board recoil? with what rate are tehboy and theboard separting from each other?
View SolutionAn air puck of mass m1 is tied to a string allowed to revolved in a circle of radius R on a frictionless horizontal table . The other end of the string passes through a small hole in the centre of the table , and a load of mass m2 is tied to the string? The suspended load remains in equilibrium while the pack on the tabletop revolves.

a. Find the tension in the string
b. Find the radial force acting on the puck
c. Find the speed of the puck
d. Qualitaively describe what will happen in the monsion of the puck if the value of m2 is somewhat increased by placing an additional load on it.
e.Qualitaively describe what will happen in the monsion of the puck if the value of m2 is instead decreased removing a part from the hanging load.
View SolutionSTATEMENT-1: One end of a string of length r is tied to a stone of mass m and the other end to a small pivot on a frictionless vertical board. The stone is whirled in a vertical circle with the pivot as the centre. The minimum speed the stone must have, when it is at the topmost point on the circle, so that the string does not slack is √gR.
because
STATEMENT-2: At the topmost point on the circle, the centripetal force is provided partly by tension in the string and partly by the weight of the stone.
View Solution
