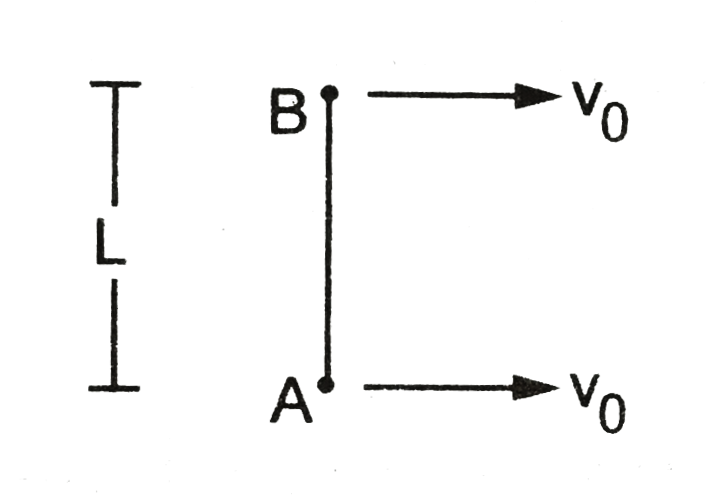
Two small balls A and B each of mass m, are joined rigidly to the ends of a light rod of length L figure. The system translates on a frictionless horizontal surface with a velocity v0 in a direction perpendicular to the rod. A particle P of mass kept at rest on the surface sticks to the ball A as the ball collides with it . Find
a. the linear speeds of the balls A and B after the collision, b. the velocity of the centre of mass C of the system A+B+P and c. the angular speed of the system about C after the collision.
The correct Answer is:A, B, C, D
Two ball A and B each of mass m are joined rigidly to the ends of a light rod of length L. The system moves with a velocity V0 in a direction perpendicular to the rod. A particle P of mass m kept at rest rod. A particle OP of masss m kept at rest on teh surface sticks to the ball A as the ball collides with it.
a. The light rod wil exert a force on the bal B only along its length. So collision will not affect its velocity.
B has a velocity =V0
if we consider the three bodies to be a system
Applying L.C.L.M.
Therefore mv0=2m×v
→v=v02
Therefore A has velocity =v02
b. If we consider the three bodies tobe a system
net exterN/Asl force =0<br>Therefore<br>V_(VCM)=(mxxv_0+2mxx(v_0/2))/(m+2m)<br>>=(mv_0+mv_0)/(3m)<br>=(2v_0)/3<br>(alongthe∈i<ialvelocityasbefoecollision)<br>c.Thevelocityof(A+P)w.r.t<br>the center of pass ={((2v_0)/3)}-(v_0-2)<br>=v_0/6<br>andthevelocityofBw.r.tthecentreofmass<br>=v_0-(2v-0)/3=v_0/3<br>(onlymagnitudehasbeentaken)<br>Distanceofthe(A+P)omcentreofmass<br>=l/3 and for B it is ((2l)/3)<br>therforeP_(cm)=L_(cm)xxomega<br>rarr 2mxxV_0/6xxl/3+mxxV_0/3xx(2l)/3
{2m(l3)2+(2l3)2m}×ω
rarr 6m(V_0l)/18=18((6ml)/9)omega<br>rarr omega=(v_0/(2l))
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective 2
15 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMACHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Exercises
51 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
Similar Questions
Two small bals A and B, each of mass m, are joined rigidlyl by a light horizontal rol of lengh L. The rod is clasmped at the centre in such a way that it c an rotate freely about a verticl axis through its centre. The systemis rotated with an angualr speed ω about the axis. A particle P of masss m kept at rest sticks to the ball A as the ball collides with it. Find the new angular speed of the rod.
View SolutionTwo small balls A and B each of mass m, are attched erighdly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View Solution
Knowledge Check
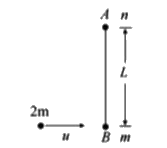
Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rod of length L. They are placed on a frictionless horizontal surface. Another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown in the figure. If the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will be
 A43ulBulC23ulDnone of these
A43ulBulC23ulDnone of these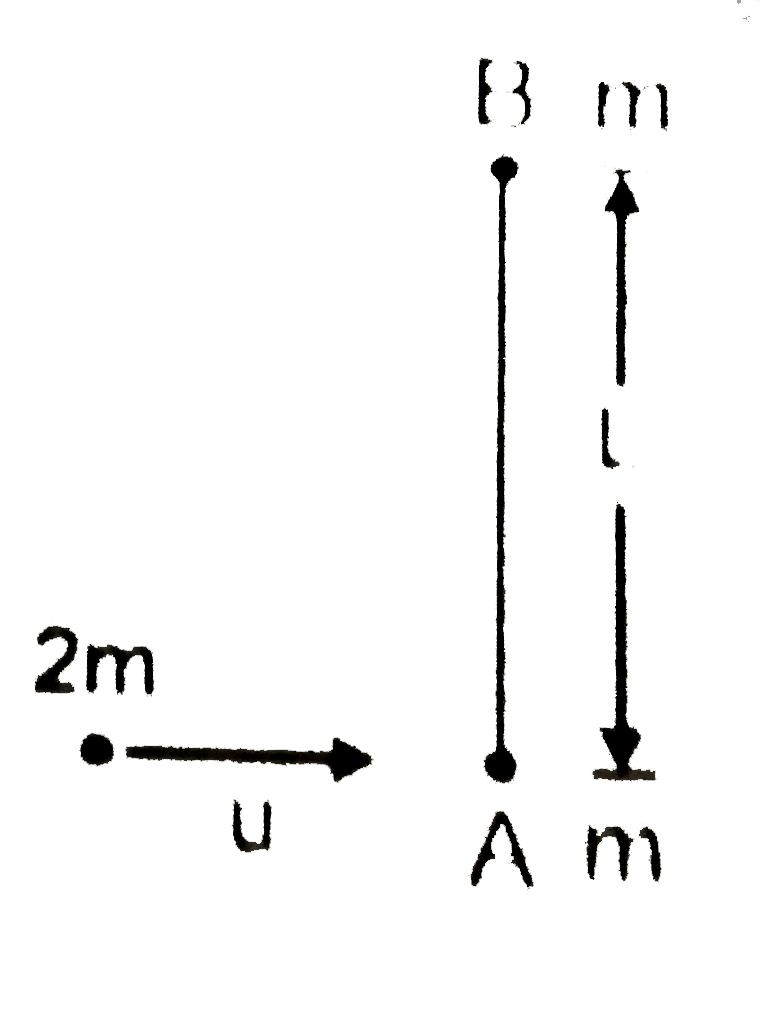
Two small balls A and B, each of mass m, are joined rigidly at the ends of a light rof of length L. they are placed on a frictionless horizontal surface another ball of mass 2 m moving with speed u towards one of the ball and perpendicular to the length of the rod on the horizontal frictionless surface as shown int he figure. if the coefficient of restitution is 1/2 then the angular speed of the rod after the collision will beA43uLBuLC23uLDnone of theseA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the centre of mass C and the angular, velocity of the system about the centre of mass after the collision.A2mvM+m,3Mv(M+2m)LBMvM+m,6Mv(M+4m)LC2mvM+m,3Mv(M+4m)LDmvM+m,6Mv(M+4m)L
A rod of mass M and length L is kept on a frictionless horizontal floor. A particle of mass m moving perpendicular to the rod with a speed v strikes at the end of the rod and sticks there. Calculate angular velocity acquired by the combined system.
View SolutionA ball of mass m is pushed with a horizontal velocity v0 from one end of a sledge of mass M and length l. if the ball stops after is first collision with the sledge, find the speeds of the ball ad sledge after the second collision of the ball with the sledge.

View SolutionTwo particles A and B, each of mass m, are connected by a light rod of length L lying on a smooth horizontal surface. A particle of mass m moving with speed v0 strikes to the end of rod and sticks to A as shown . Find
(a) the velocity of the center of mass,
(b) the angular velocity about the center of mass of system (A+B+ particle) and
(c) the linear speeds of A and B immediately after collision.

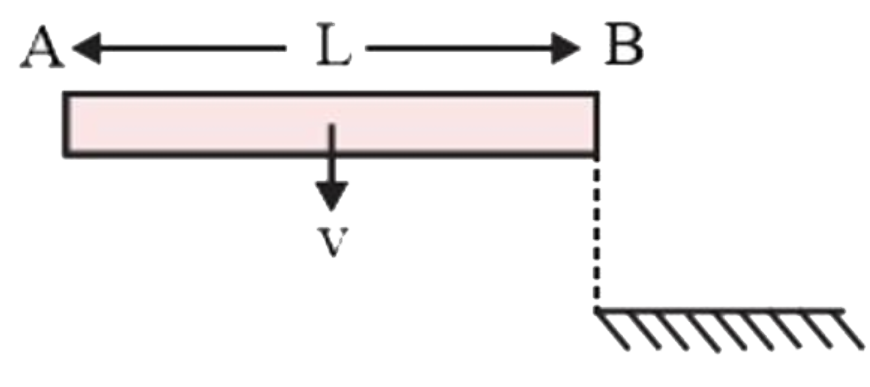
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface . It is moving with a velocity v , as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact , the angular velocity of the rod AB , just after
View SolutionA uniform rod lies at rest on a frictionless horizontal surface. A particle, having a mass equal to that of the rod, moves on the surface perpendicular to the rod collides with it, and finally sticks to it. The minimum loss of KE in the collision , under the given conditions, is
View Solution
