A frog sits on the end pf a long boord of length L. the boord rests on a fricationless horizontal table. The frog wants os the minimum takes - off speed i.e relative to ground v that allows the frog yo do the trick? The board and the frog have equal masses.
The correct Answer is:2
Apply conservation of momentum in horizontal direction
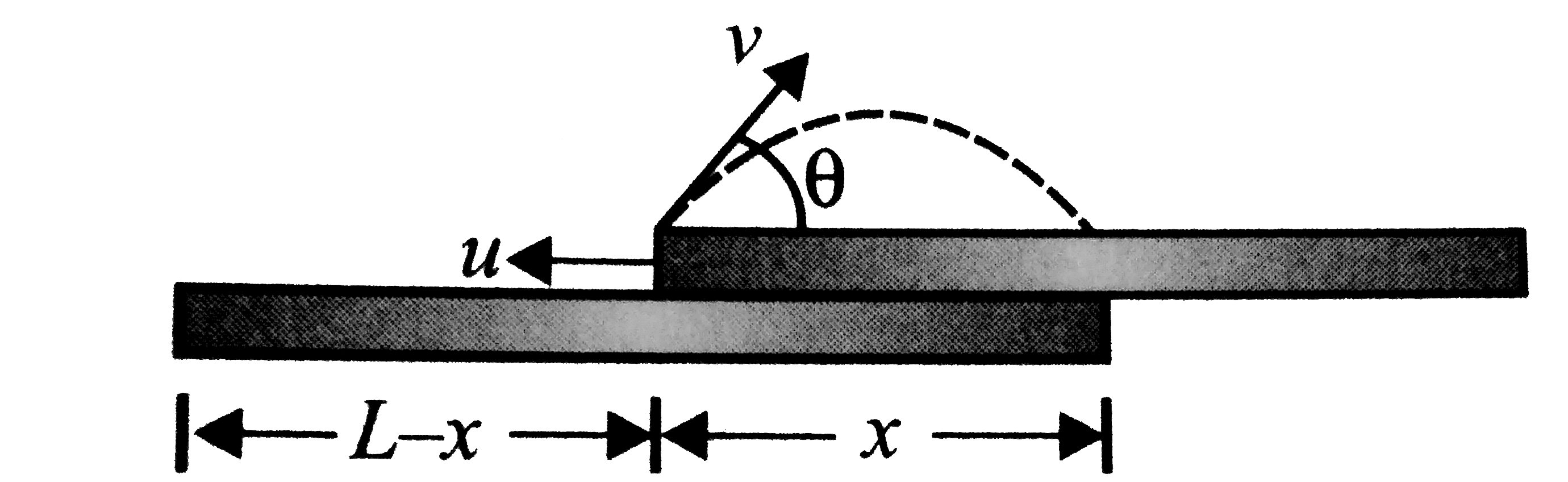
mvcosθ−μ=0⇒u=vcosθ
L−x,ut,xv=vcosθt
Solve to get x=L2
x=v2sin2θg⇒L2=v2sin2θg
⇒v=(gL2sinθ) for minimum v,sin2θ=1
⇒v=√gL2=√10×52=2s√5m/s, Hence n=2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Fill In The Blanks
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - SCQ_TYPE
12 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Linked Comprehension
105 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A table cloth of length L is lying on a table with one of its end at the edge of the table. A block is kept at the centre of the table cloth. A man pulls the end of the table cloth horizontally so as to take it off the table. The cloth is pulled at a constant speed V0. What can you say about the coefficient of friction between the block and the cloth if the block remains on the table (i.e., it does not fall off the edge) as the cloth is pulled out.
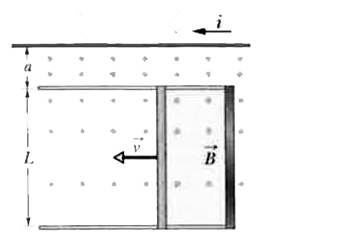
View SolutionFigure 30-50 shows a rod of length L = 12.0 cm that is forced to move at constant speed v = 5.00 m/s along horizontal rails. The rod, rails, and connecting strip at the right form a conducting loop. The rod has resistance 0.400 Ω the rest of the loop has negligible resistance. A current i = 100 A through the long straight wire at distance a= 5.00 mm from the loop sets up a (nonuniform) magnetic field through the loop. Find the (a) emf and (b) current induced in the loop. (c) At what rate is thermal energy generated in the rod? (d) What is the magnitude of the force that must be applied to the rod to make it move at constant speed? (e) At what rate does this force do work on the rod?
View Solution
Knowledge Check
A uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.
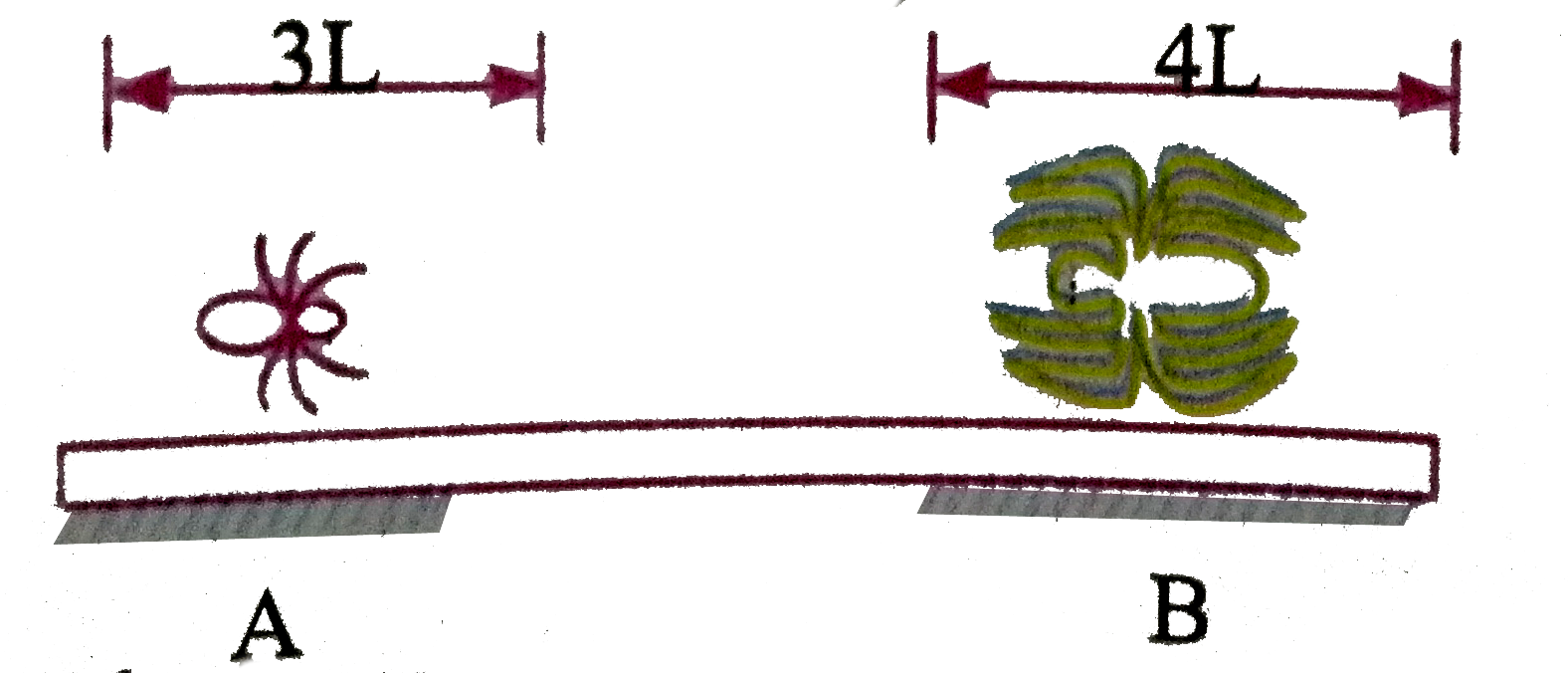
The speed of the bar after the spider eats up the moth and moves towards A isAv/2BvCv/6D2vA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.
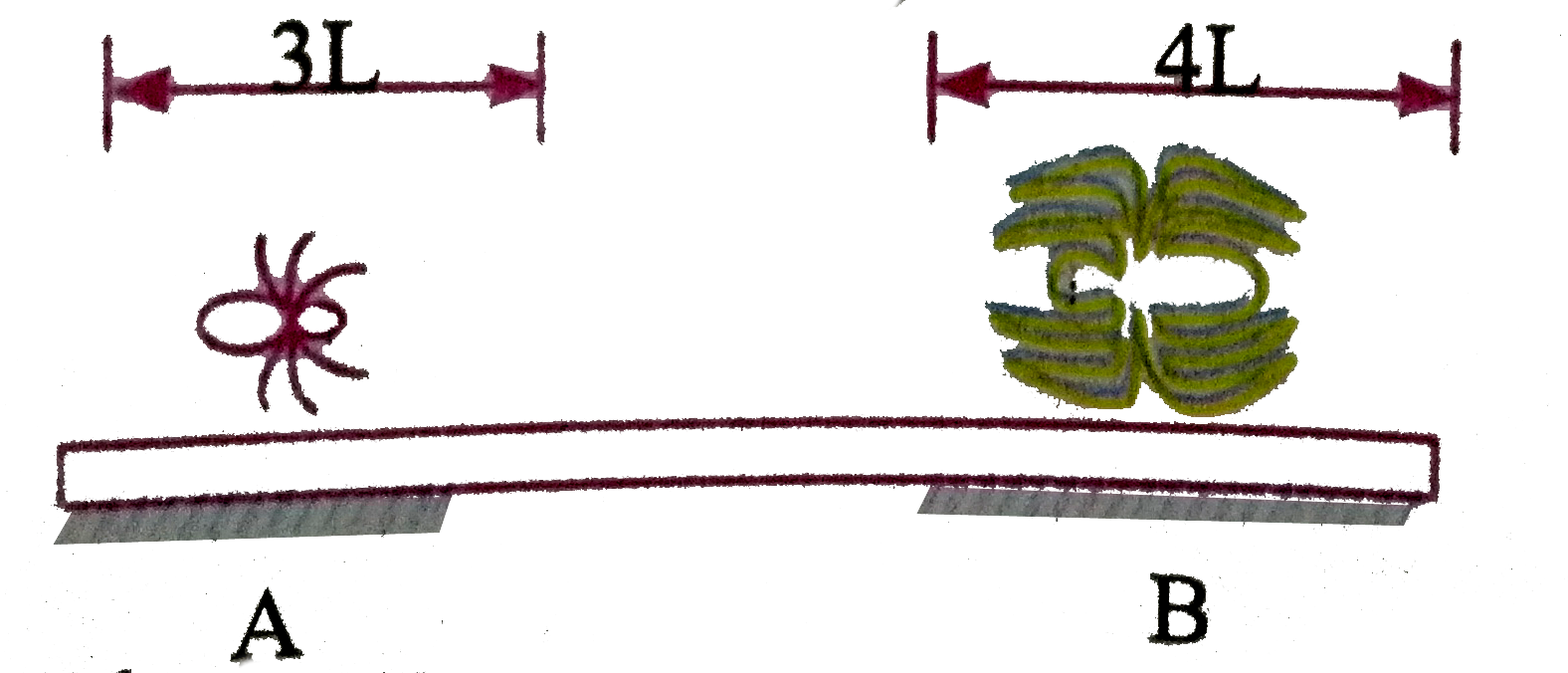
The point P is atAthe centre of the rodBthe edge of the table supporting the end BCclose to the edge of the table supporting the end ADnone of the aboveA uniform bar of length 12L and mass 48m is supported horizontally on two smooth tables as shown in the figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects start moving towards each other along the rod with moth moving at speed 2v and the spider at half of this speed. They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v/2 relative to the rod towards the end A. The spider takes negligible time in eating the insect. Also, let v=L/T, where T is a constant having value 4sec.
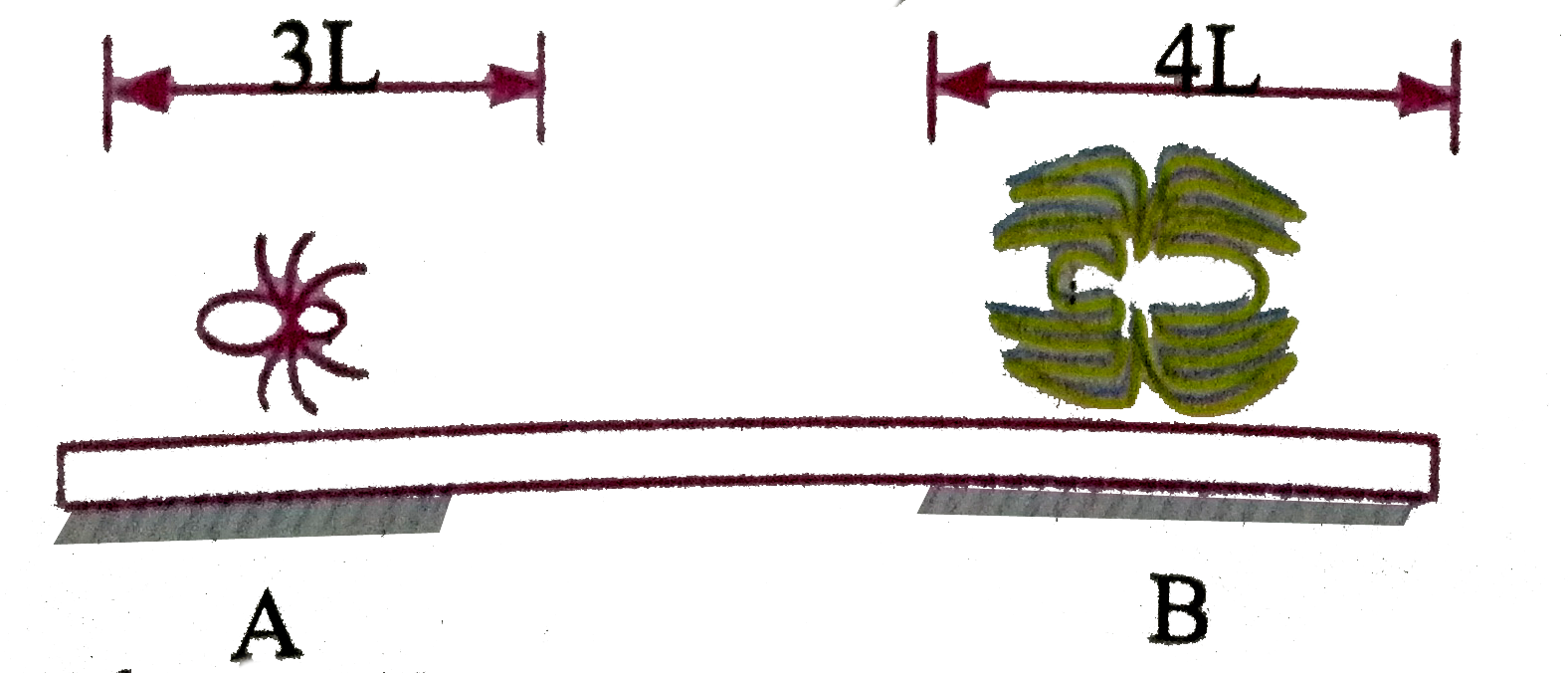
Displacement of the rod by the time when the insects meet isAL/2BLC3L/4Dzero
Figure shows a wire ab of length L and resistance R which can slide on a smooth pair of rails. Ig is current generator which supplies a constant current i in the circuit. If the wire ab slide at a speed v towards right, find the potential difference below a and b

(b) The current generator Ig show in the figure sends a constant current i through the circiut. The wire ab has a length L and mass m and can slide on the smooth horizontal rails connect to Ig . The entire system lies in a vertical magnetic field B . Find the velocity of the wire as a function of time.

(c) The system containing the rails and the wire of the previous part is kept vertically in a uniform horizontal magnetic field B that is perpendicular to the plane of the rails (figure). If is found that the wire stays in equilibrium. If th ewire ab is replaced by another wire of double its mass, how long will lit take in falling through a distance equal to its length?
The current generator Ig shown in figure sends a constant current i through the circuit. The wire cd is fixed and wire ab is made to slide on the smooth, thick rails with a constant velocity v toward right. Each of these wires has resistance r . Find the current through the wire cd .

View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
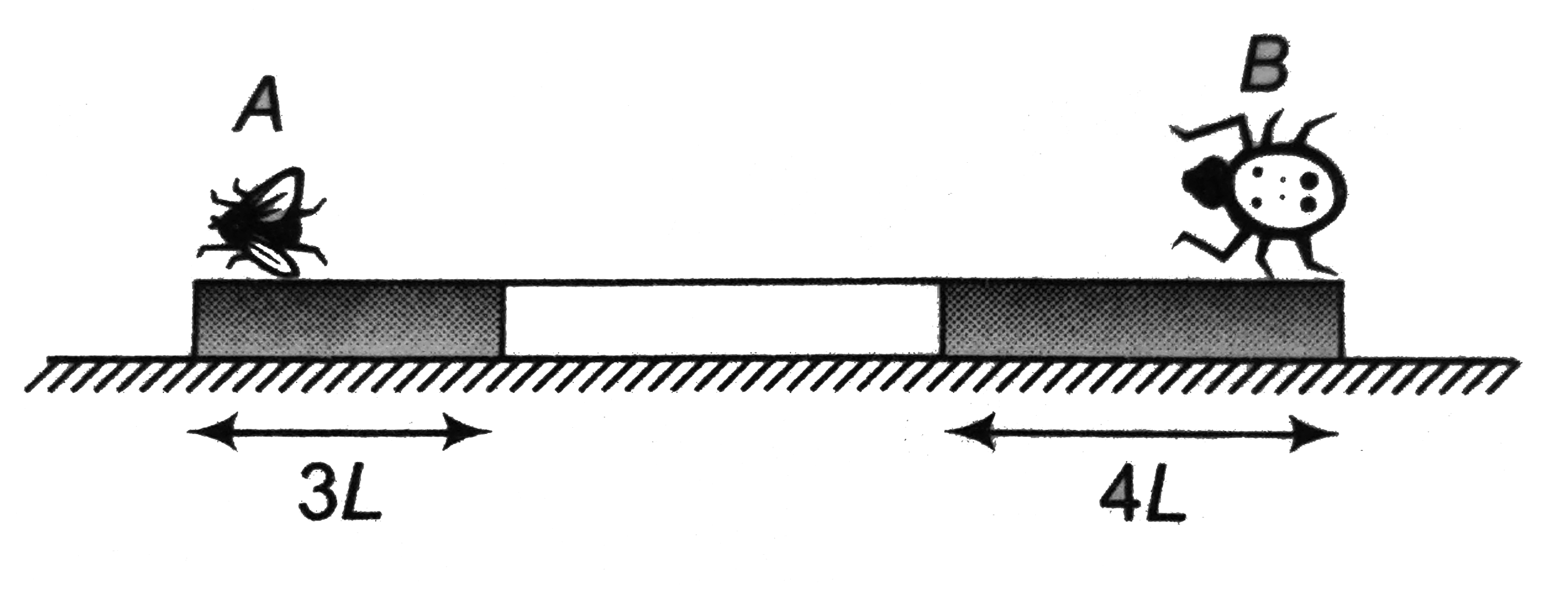
After starting from end B of the rod the spider reaches the end A at a time
View SolutionA uniform bar of length 12L and mass 48m is supported horizontally on two fixed smooth tables as shown in figure. A small moth (an insect) of mass 8m is sitting on end A of the rod and a spider (an insect) of mass 16m is sitting on the other end B. Both the insects moving towards each other along the rod with moth moving at speed 2v and the spider at half this speed (absolute). They meet at a point P on the rod and the spider eats the moth. After this the spider moves with a velocity v2 relative to the rod towards the end A. The spider takes negligible time in eating on the other insect. Also, let v=LT where T is a constant having value 4s.
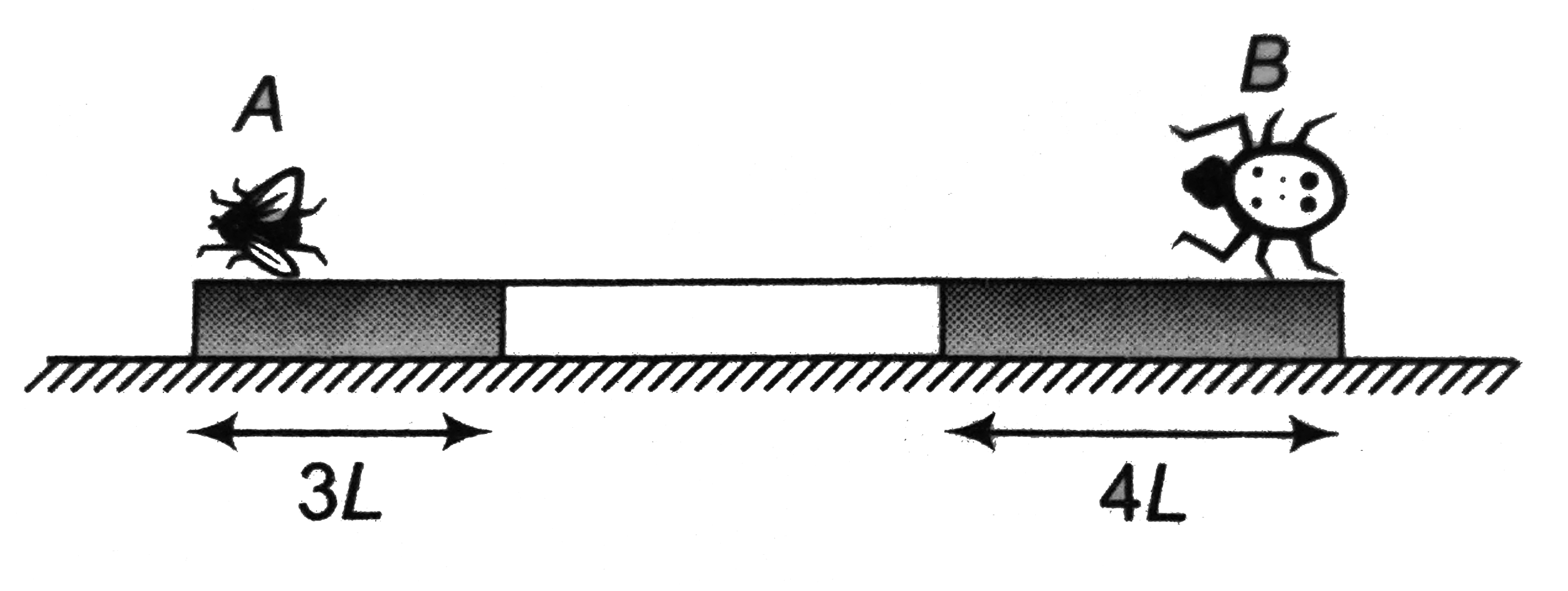
By what distance the centre of mass of the rod shifts during this time?
View SolutionRead the passage and answer the questions given below it
No one can look back on his schooldays and say with truth that they were altogether unhappy. I have good memories of St Cyprian's, among a horde of bad ones. Sometimes on summer afternoons there were wonderful expeditions across the Downs to a village called Birling Gap, or to Beachy Head, where one bathed dangerously among the boulders and came home covered with cuts. And there were still more wonderful mid-summer evenings when, as a special treat, we were not driven off to bed as usual but allowed to wander about the grounds in the long twilight, ending up with a plunge into the swimming bathe at about nine o'clock. There was the joy of waking early on summer mornings and getting in an hour's undisturbed reading (Ian Hay, Thackeray, Kipling and H. G. Wells were the favourite authors of my boyhood) in the sunlit, sleeping dormitory. There was also cricket, which I was no good at but with which I conducted a sort of hopeless love affair up to the age of about eighteen. And there was the pleasure of keeping caterpillars — the silky green and purple puss-moth, the ghostly green poplar-hawk, the privet-hawk, large as one's third finger, specimens of which could be illicitly purchased for sixpence at a shop in the town — and, when one could escape long enough from the master who was ‘taking the walk’, there was the excitement of dredging the dew-ponds on the Downs for enormous newts with orange-coloured bellies. This business of being out for a walk, coming across something of fascinating interest and then being dragged away from it by a yell from the master, like a dog jerked onwards by the leash, is an important feature of school life, and helps to build up the conviction, so strong in many children, that the things you most want to do are always unattainable.
Which of the following did the boys not do on summer mornings?
View SolutionRead the passage and answer the questions given below it.
No one can look back on his schooldays and say with truth that they were altogether unhappy. I have good memories of St Cyprian.s, among a horde of bad ones. Sometimes on summer afternoonsthere were wonderful expeditions across the Downs to a village called Birling Gap, or to Beachy Head, where one bathed dangerously among the boulders and came home covered with cuts. And there were still more wonderful midsummer evenings when, as a special treat, we were not driven off to bed as usual but allowed to wander about the grounds in the long twilight, ending up with a plunge into the swimming bathe at about nine o.clock. There was the joy of waking early on summer mornings and getting in an hour.s undisturbed reading (Ian Hay, Thackeray, Kipling and H. G. Wells were the "favourite authors of my boyhood) in the sunlit, sleeping dormitory. There was also cricket, which I was no good at but with which I conducted a sort of hopeless love affair up to the age of about eighteen. And there was the pleasure of keeping caterpillars-the silky green and purple puss-moth, the ghostly green poplar-hawk, the privet-hawk, large as one.s third finger, specimens of which could be illicitly purchased for sixpence ata shop in the town - and, when one could escape long enough from the master who was .taking the walk., there was the excitement of dredging the dew-ponds on the Downs for enormous newts with orange coloured bellies. This business of being out for a walk, coming across something of fascinating interest and then being dragged away from it by a yell from the master, like a dog jerked onwards by the leash, is an important feature of school life, and helps to build up the conviction, so strong in many children, that the things you most want to do are always unattainable.
Which of the following did the boys not do on summer mornings?
View Solution
