A gas at 300 K has pressure 4×10−10N/m2. IF k=1.38×10−23J/K, the number of molecule/cm3 is of the order of
103
105
106
109
The correct Answer is:B
To find the number of molecules per cubic centimeter in a gas at a given temperature and pressure, we can use the relation derived from the ideal gas law. Here’s a step-by-step solution:
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by:
PV=nRT
where:
- P = pressure,
- V = volume,
- n = number of moles,
- R = universal gas constant,
- T = temperature in Kelvin.
Step 2: Relate Moles to Molecules
We know that:
n=NNA
where N is the number of molecules and NA is Avogadro's number.
Step 3: Use Boltzmann's Constant
We can express the ideal gas law in terms of the number of molecules:
PV=NkT
where k is Boltzmann's constant. Rearranging gives:
N=PVkT
Step 4: Convert Units
Since we need the number of molecules per cubic centimeter, we need to convert the pressure from N/m2 to N/cm2:
1m2=104cm2
Thus, the pressure in N/cm2 is:
P=4×10−10N/m2=4×10−10N/m2×1104=4×10−14N/cm2
Step 5: Substitute Values
Now, substituting the values into the equation:
N=PkT
where:
- P=4×10−14N/cm2,
- k=1.38×10−23J/K,
- T=300K.
Step 6: Calculate N
Now we can calculate N:
N=4×10−14(1.38×10−23)(300)
Calculating the denominator:
1.38×10−23×300=4.14×10−21
Now substituting back:
N=4×10−144.14×10−21≈9.66×106molecules/cm3
Step 7: Order of Magnitude
The order of magnitude of N is approximately 107 molecules/cm³.
Final Answer
Thus, the number of molecules per cubic centimeter is of the order of 107.
The ideal gas law is given by:
PV=nRT
where:
- P = pressure,
- V = volume,
- n = number of moles,
- R = universal gas constant,
- T = temperature in Kelvin.
We know that:
n=NNA
where N is the number of molecules and NA is Avogadro's number.
We can express the ideal gas law in terms of the number of molecules:
PV=NkT
where k is Boltzmann's constant. Rearranging gives:
N=PVkT
Since we need the number of molecules per cubic centimeter, we need to convert the pressure from N/m2 to N/cm2:
1m2=104cm2
Thus, the pressure in N/cm2 is:
P=4×10−10N/m2=4×10−10N/m2×1104=4×10−14N/cm2
Now, substituting the values into the equation:
N=PkT
where:
- P=4×10−14N/cm2,
- k=1.38×10−23J/K,
- T=300K.
Now we can calculate N:
N=4×10−14(1.38×10−23)(300)
Calculating the denominator:
1.38×10−23×300=4.14×10−21
Now substituting back:
N=4×10−144.14×10−21≈9.66×106molecules/cm3
The order of magnitude of N is approximately 107 molecules/cm³.
Thus, the number of molecules per cubic centimeter is of the order of 107.
Topper's Solved these Questions
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Kinetic Theory of An Ideal Gas
Explore 18 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:LAW OF EQUIPARTITION OF ENERGY
Explore 5 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Assertion And Reason
Explore 15 Videos
- LAWS OF MOTIONBook:NCERT FINGERTPS ENGLISHChapter:LAWS OF MOTIONExercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A cubical box of side 1m contains helium gas (atomic weight 4) at a pressure of 100N/m2. During an observation time of 1second, an atom travelling with the root - mean - square speed parallel to one of the edges of the cube, was found to make 500hits with a particular wall, without any collision with other atoms . Take R=253j/mol−Kandk=1.38×10−23J/K.
Evaluate the total mass of helium gas in the box.
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
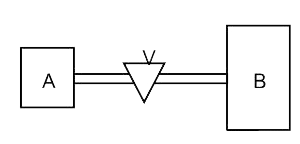
Before the valve V is opened, the ratio of number of moles of gas in A and B is :
View Solution
Knowledge Check
The Henry's law constant for the solubility of N2 gas in water at 298K is 1.0×105atm. The mole fraction of N2 in air is 0.8. The number of moles of N2 from air dissolved in 10 moles of water at 298K and 5atm. Pressure is:
A4.0×10−4B4.0×10−5C5.0×10−4D4.0×10−6
Calculate the K.E. per mole of oxygen at 27∘C. Given N=6.02×1023,k=1.38×10−23JK−1.
View SolutionA cubical box of side 1m contains helium gas (atomic weight 4) at a pressure of 100N/m2. During an observation time of 1second, an atom travelling with the root - mean - square speed parallel to one of the edges of the cube, was found to make 500hits with a particular wall, without any collision with other atoms . Take R=253j/mol−Kandk=1.38×10−23J/K.
Evaluate the temperature of the gas.
View SolutionThe Henry's law constant for the solubility of N2 gas in water at 298K is 1.0×105 atm. The mole fraction of N2 in air is 0.8. The number of moles of N2 from air dissolved in 10 moles of water at 298K and 5 atm pressure is
View SolutionA flask contains 10−3m3 gas. At a temperature, the number of molecules of oxygen at 3.0×1022. The mass of an oxygen molecule is 5.3×10−26 kg and at that temperature the rms velocity of molecules is 400m/s. The pressure in N/m2 of the gas in the flask is ..............
View SolutionThe root mean square speed of gas molecules at a temperature 27K and pressure 1.5 bar is 1×104cm/sec If both temperature and pressure are raised three times calculate the new rms speed of gas molecules .
View SolutionA sample of air weighing 1.18g occupies 1.0×103cm3 when kept at 300Kand1.0×105 pa. When 2.0cal of heat is added to it constant volume, its temperature increases by 1∘C. Calculate the amount if heat needed to increases the temperature of air by 1∘C at constant pressure if the mechanical equivalent of heat si 4.2×10−1 . Assume that air behaves as an ideal gas.
View SolutionOne mole of an ideal gas is kept enclosed under a light piston (area =10−2m2) connected by a compresses spring (spring constant 100N/m). The volume of gas is 0.83m3 and its temperature is 100K. The gas is heated so that it compresses the spring further by 0.1m. The work done by the gas in the process is N×10−1J. Find N. (Take R=8.3J/K−mole) and suppose there is no atmosphere).
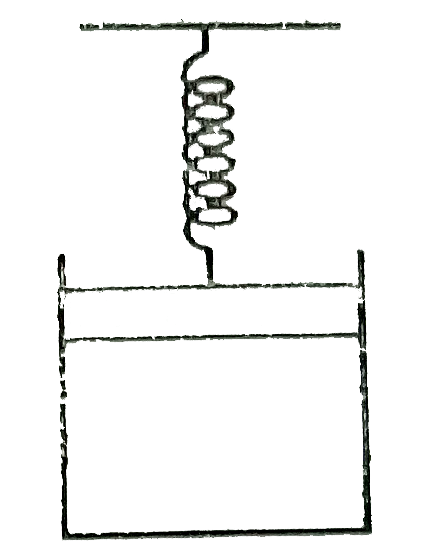
View Solution