A germanium slab of cuboidal shape with dimensions 10cm×15cm×0.1cm is coated with a thin layer of metal on two parallel sides. Calculate the capacitance across the metal plates given that the dielectric constant of germanium is 16.
To calculate the capacitance across the metal plates of a germanium slab, we will follow these steps:
Step 1: Identify the dimensions of the slab
The dimensions of the germanium slab are given as:
- Length (l) = 10 cm = 0.1 m
- Width (w) = 15 cm = 0.15 m
- Thickness (d) = 0.1 cm = 0.001 m
Step 2: Calculate the area of the plates
The area (A) of the plates can be calculated using the formula:
A=l×w
Substituting the values:
A=0.1m×0.15m=0.015m2
Step 3: Identify the dielectric constant
The dielectric constant (K) of germanium is given as:
K=16
Step 4: Use the formula for capacitance
The capacitance (C) of a parallel plate capacitor with a dielectric is given by the formula:
C=K⋅A⋅ϵ0d
where:
- ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m
- d is the separation between the plates (thickness of the slab)
Step 5: Substitute the values into the capacitance formula
Substituting the values we have:
C=16⋅0.015m2⋅8.85×10−12F/m0.001m
Step 6: Calculate the capacitance
Calculating the numerator:
16⋅0.015⋅8.85×10−12=2.1168×10−13F
Now, divide by d:
C=2.1168×10−130.001=2.1168×10−10F
Step 7: Convert to nanoFarads
To convert Farads to nanoFarads (1 F = 109 nF):
C=2.1168×10−10F=21.168nF
Final Answer
The capacitance across the metal plates is approximately:
C≈21.17nF
---
The dimensions of the germanium slab are given as:
- Length (l) = 10 cm = 0.1 m
- Width (w) = 15 cm = 0.15 m
- Thickness (d) = 0.1 cm = 0.001 m
The area (A) of the plates can be calculated using the formula:
A=l×w
Substituting the values:
A=0.1m×0.15m=0.015m2
The dielectric constant (K) of germanium is given as:
K=16
The capacitance (C) of a parallel plate capacitor with a dielectric is given by the formula:
C=K⋅A⋅ϵ0d
where:
- ϵ0 (the permittivity of free space) is approximately 8.85×10−12F/m
- d is the separation between the plates (thickness of the slab)
Substituting the values we have:
C=16⋅0.015m2⋅8.85×10−12F/m0.001m
Calculating the numerator:
16⋅0.015⋅8.85×10−12=2.1168×10−13F
C=2.1168×10−130.001=2.1168×10−10F
To convert Farads to nanoFarads (1 F = 109 nF):
C=2.1168×10−10F=21.168nF
The capacitance across the metal plates is approximately:
C≈21.17nF
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 518videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Conceptual Questions37videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - PRACTICE PROBLEMS 33videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure from a cuboidal solid metallic block of dimensions 15cm×10cm×5cm a cylindrical hole of diamter 7 cm is drilled out . Find the suface area of the remaining block .
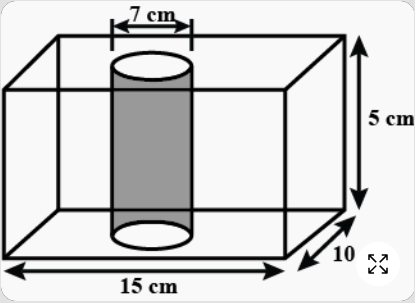 A450cm2B553cm2C550cm2D583cm2
A450cm2B553cm2C550cm2D583cm2
A cuboidal tin box opened at the top has dimensions 20cm×16cm×14cm. What is the total area of metal sheet required to make 10 such boxes?
View SolutionA cuboid is of dimensions 60cm×54cm×30cm.How many small cubes with side 6 cm can be placed in the given cuboid?
View SolutionThe dimensions of a cuboid are 15 cm × 12 cm × 10 cm . What is its total surface area ?
View SolutionWhat is the volume of a cuboid of dimensions 2.8 cm × 1.6 cm × 4 cm?
View SolutionA parallel plate capacitor with each plate of dimension 10cm×15cm and a plate separation of 0.2 cm is filled with two slabs of dielectric media as shown in the figure. Calculate the capacitance of the capacitor if K1=6andK2=9.
 View Solution
View SolutionA rectangular block of iron has dimension 1.2cm×1.2cm×1.5cm. A potential difference is to be applied to the block between parallel sides and in such a way that those sides are equipotential surfaces. What is the resistance of the block if the two parallel sides are (1) the square ends (with dimensions 1.2cm×1.2cm) and (2) two rectangular sides (with dimensions 1.2cm×15cm)?
View SolutionThe plates of a parallel plate capacitance 1.0 F are separated by a distance d =1 cm. Find the plate area .
View Solution

