A girl dropped an orange in a moving bus with acceleration a, what will be the acceleration of the apple with respect to the bus?
To solve the problem of finding the acceleration of the orange with respect to the moving bus, we can follow these steps:
Step 1: Understand the scenario
The girl drops an orange from a moving bus. The bus has an acceleration a (which is given as 8 m/s² in the video transcript). When the orange is dropped, it will have two components of acceleration: the acceleration of the bus and the acceleration due to gravity.
Step 2: Identify the accelerations
- The acceleration of the bus, a, is in the horizontal direction (let's assume it is in the positive x-direction).
- The acceleration of the orange due to gravity, g, is acting downwards (in the negative y-direction).
Step 3: Represent the accelerations as vectors
- The acceleration of the bus can be represented as:
→abus=a^i(where ^i is the unit vector in the x-direction)
- The acceleration of the orange (just before it is dropped) is:
→aorange=0^i−g^j(where ^j is the unit vector in the y-direction)
Step 4: Calculate the acceleration of the orange with respect to the ground
When the orange is dropped, its acceleration with respect to the ground is simply the acceleration due to gravity, which is:
→aorange=−g^j
Step 5: Calculate the acceleration of the orange with respect to the bus
The acceleration of the orange with respect to the bus can be calculated using the formula:
→aorange, bus=→aorange−→abus
Substituting the values:
→aorange, bus=(−g^j)−(a^i)=−g^j−a^i
Step 6: Determine the magnitude and direction
The resultant acceleration vector has components in both the x and y directions:
- The x-component is −a
- The y-component is −g
To find the magnitude of the acceleration of the orange with respect to the bus, we use the Pythagorean theorem:
|→aorange, bus|=√(−a)2+(−g)2=√a2+g2
Step 7: Conclusion
The acceleration of the orange with respect to the bus is directed downward and has a magnitude given by:
|→aorange, bus|=√a2+g2
The girl drops an orange from a moving bus. The bus has an acceleration a (which is given as 8 m/s² in the video transcript). When the orange is dropped, it will have two components of acceleration: the acceleration of the bus and the acceleration due to gravity.
- The acceleration of the bus, a, is in the horizontal direction (let's assume it is in the positive x-direction).
- The acceleration of the orange due to gravity, g, is acting downwards (in the negative y-direction).
- The acceleration of the bus can be represented as:
→abus=a^i(where ^i is the unit vector in the x-direction)
- The acceleration of the orange (just before it is dropped) is:
→aorange=0^i−g^j(where ^j is the unit vector in the y-direction)
When the orange is dropped, its acceleration with respect to the ground is simply the acceleration due to gravity, which is:
→aorange=−g^j
The acceleration of the orange with respect to the bus can be calculated using the formula:
→aorange, bus=→aorange−→abus
Substituting the values:
→aorange, bus=(−g^j)−(a^i)=−g^j−a^i
The resultant acceleration vector has components in both the x and y directions:
- The x-component is −a
- The y-component is −g
|→aorange, bus|=√(−a)2+(−g)2=√a2+g2
The acceleration of the orange with respect to the bus is directed downward and has a magnitude given by:
|→aorange, bus|=√a2+g2
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - REVISION EXERCISE (FILL IN THE BLANKS)
10 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - REVISION EXERCISE (SHORT ANSWER QUESTIONS)
19 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - HIGHER ORDER THINKING SKILL AND ADVANCED LEVEL QUESTION WITH ANSWER
5 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - Chapter Practice Test
15 Videos
- OSCILLATIONS BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - Practice Test (For Board Examination)
12 Videos
Similar Questions
Find the acceleration of an orange fallen in a bus moving with acceleration a, with respect to the road.
View SolutionA railway carriage moves over a straight track with acceleration a. Passenger in the carriage drops a stone. What is the acceleration of the stone w.r.t. the carriage and the earth?
View Solution
Knowledge Check
A ball is dropped from an elevator moving upward with acceleration 'a' by a boy standing in it. The acceleration of ball with respect to [Take upward direction positive]
ABoy is - gBBoy is −(g+a)CGround is −gDBoth (2) & (3)A lift moves downwards with an acceleration a. A passenger in the lift drops a book. The acceleration of the book with respect to the floor of lift is-
(assume acceleration due to gravity = g)AgBaCg−aDg+aIf A and B moves with acceleration a block c moves up with acceleration b calculate acceleration of D with respective A.
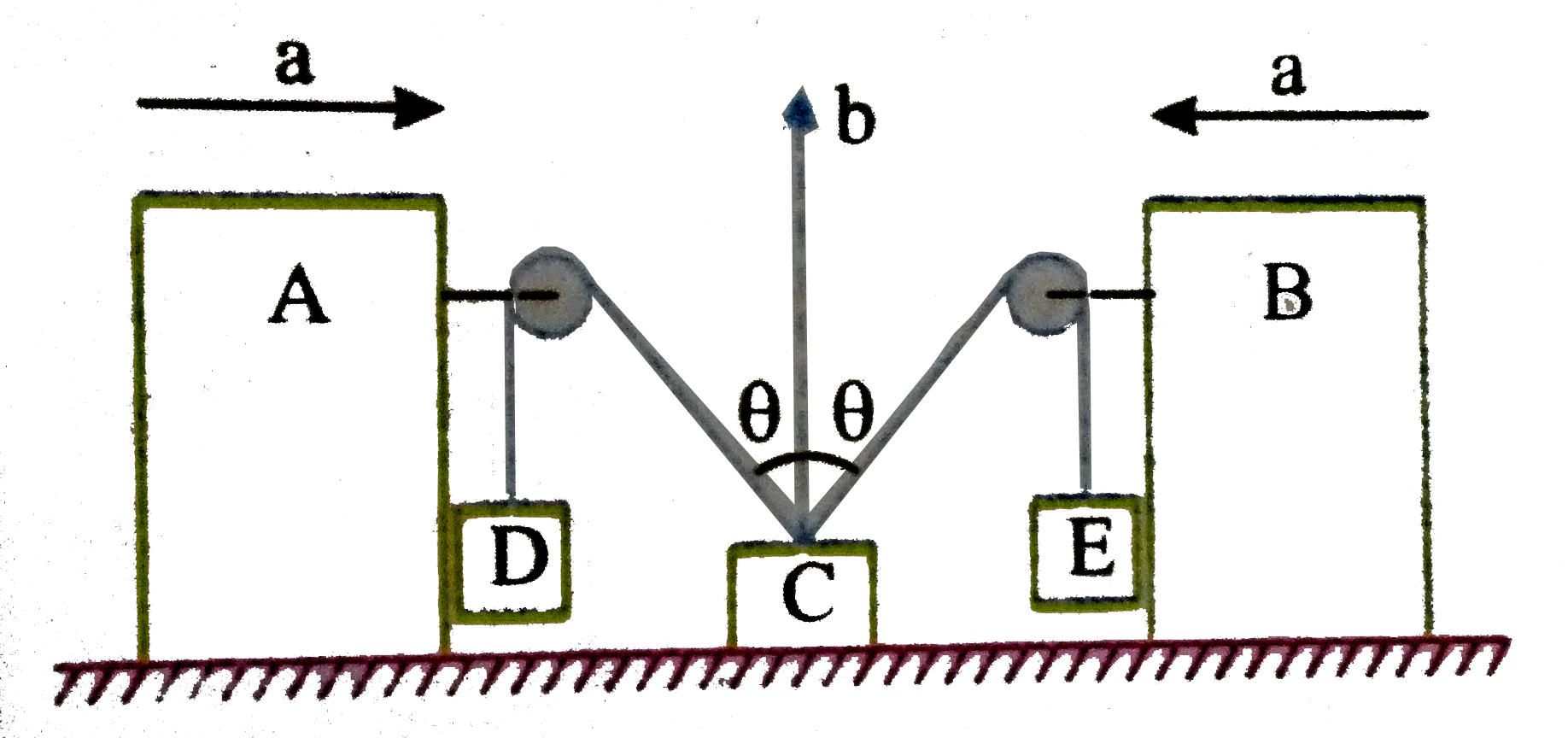 .A2a+bB2a+bcosθCbcosθ+asinθDbsinθ+acosθ
.A2a+bB2a+bcosθCbcosθ+asinθDbsinθ+acosθ
A bus moves over a straight level road with a constant acceleration a. A boy in the bus drops a ball out side. The acceleration of the ball w.r.t the bus and the earth are respectively
View SolutionA lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
View SolutionA lift is moving down with acceleration a. A man in the lift drops a ball inside the lift. The acceleration of the ball as observed by the man in the lift and a man standing stationary on the ground are respectively
View SolutionA bus starts from rest and moves whith acceleration a=2ms2. The ratio of the distance covered in 6th second to that covered in 6 seconds is
View SolutionA car is standing 800 m behind a bus, which is also at rest. The two start moving at the same instant but the different forward accelerations. The bus has acceleration 4m/s2 and the car has acceleration 8m/s2. The car will catch up with the bus after a time of:
View Solution
