A glass ball collides with a smooth horizontal surface ( plane) with a velocity . If the coefficient of restitution of collision be , the velocity of the ball just after the collision will be
at angle to the vertical
at angle to the vertical
at angle to the vertical
at angle to the vertical
The correct Answer is:B
To solve the problem of determining the velocity of a glass ball just after it collides with a smooth horizontal surface, we can follow these steps:
1. Identify the Initial Velocity:
The initial velocity of the ball is given as V=a^i−b^j, where a is the component in the x-direction and −b is the component in the y-direction.
2. Understand the Collision:
The collision occurs with a smooth horizontal surface (the xz-plane). The normal to this surface is in the y-direction. Therefore, the y-component of the velocity will be affected by the collision, while the x-component will remain unchanged.
3. Apply the Coefficient of Restitution:
The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach. For a collision with a surface, the velocity of approach is the negative of the y-component of the incoming velocity, which is b.
e=Velocity of separationVelocity of approach=vy,afterb
4. Determine the Velocity of Separation:
From the equation above, we can express the velocity of separation in the y-direction after the collision:
vy,after=e⋅b
Since the ball is moving upwards after the collision, the direction of this component will be positive.
5. Combine the Components of Velocity After Collision:
The final velocity of the ball after the collision can be expressed as:
Vfinal=a^i+eb^j
Here, a^i remains unchanged, and eb^j is the new y-component of the velocity.
6. Conclusion:
The velocity of the ball just after the collision is:
Vfinal=a^i+eb^j
The initial velocity of the ball is given as V=a^i−b^j, where a is the component in the x-direction and −b is the component in the y-direction.
The collision occurs with a smooth horizontal surface (the xz-plane). The normal to this surface is in the y-direction. Therefore, the y-component of the velocity will be affected by the collision, while the x-component will remain unchanged.
The coefficient of restitution e is defined as the ratio of the velocity of separation to the velocity of approach. For a collision with a surface, the velocity of approach is the negative of the y-component of the incoming velocity, which is b.
From the equation above, we can express the velocity of separation in the y-direction after the collision:
The final velocity of the ball after the collision can be expressed as:
The velocity of the ball just after the collision is:
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Multiple Correct
25 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Assertion - Reasoning
2 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Subjective
23 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e.
(a) Find expression for the velocity of the ball immediately after the impact.
(b) If impact is perfectly elastic what do you observe?
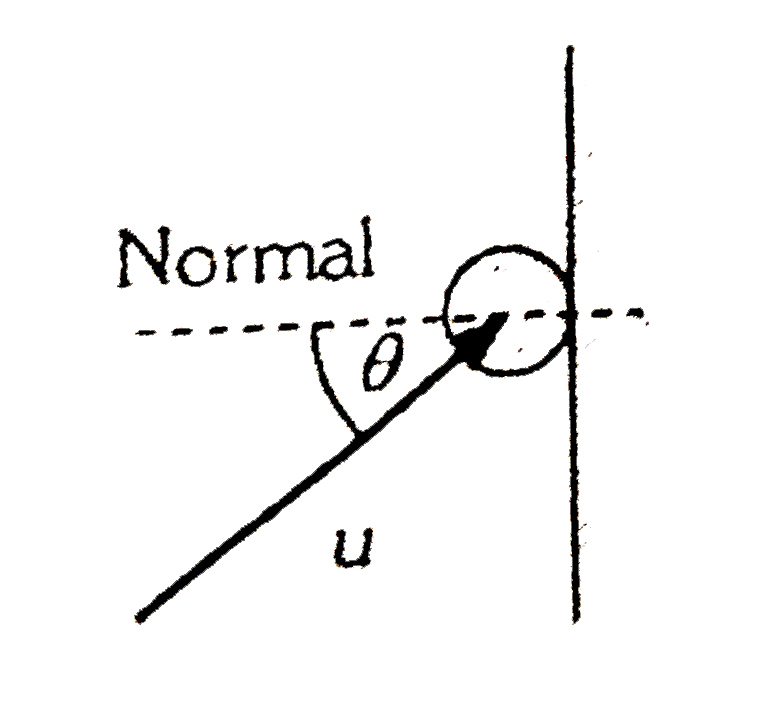
View Solution
Knowledge Check
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1
A ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

View SolutionA ball P is moving with a certain velocity v, collides head-on with another ball Q of same mass at rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View SolutionA small ball of mass m collides with as rough wal having coeficient of friction μ at an angle θ with the normal to the wall. If after collision the ball moves wilth angle α with the normal to the wall and the coefficient of restitution is e, then find the reflected velocity v of the ball just after collision.

View SolutionA ball collides elastically with a massive wall moving towards it with a velocity of v as shown. The collision occurs at a height of h above ground level and the velocity of the ball just before collision is 2v in horizontal direction. The distance between the foot of the wall and the point on the ground where the ball lands, at the instant the ball lands, will be :
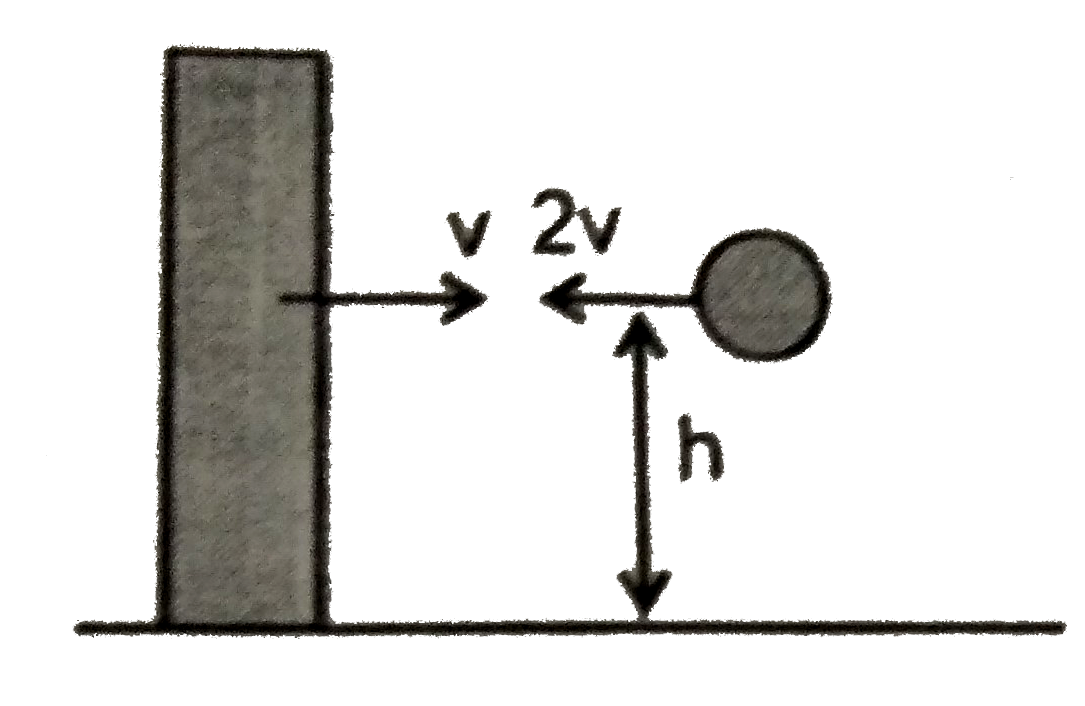
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View SolutionA ball moving with velocity 2ms−1 collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in ms−1) after collision will be
View Solution
