A glass shere of radius 2R, refractive index n has a spherical cavity of radius R, concentric with it. A black spot on the inner surface of the hollow sphere is viewed from the left as well as right. Obtain the shift in position of the object.
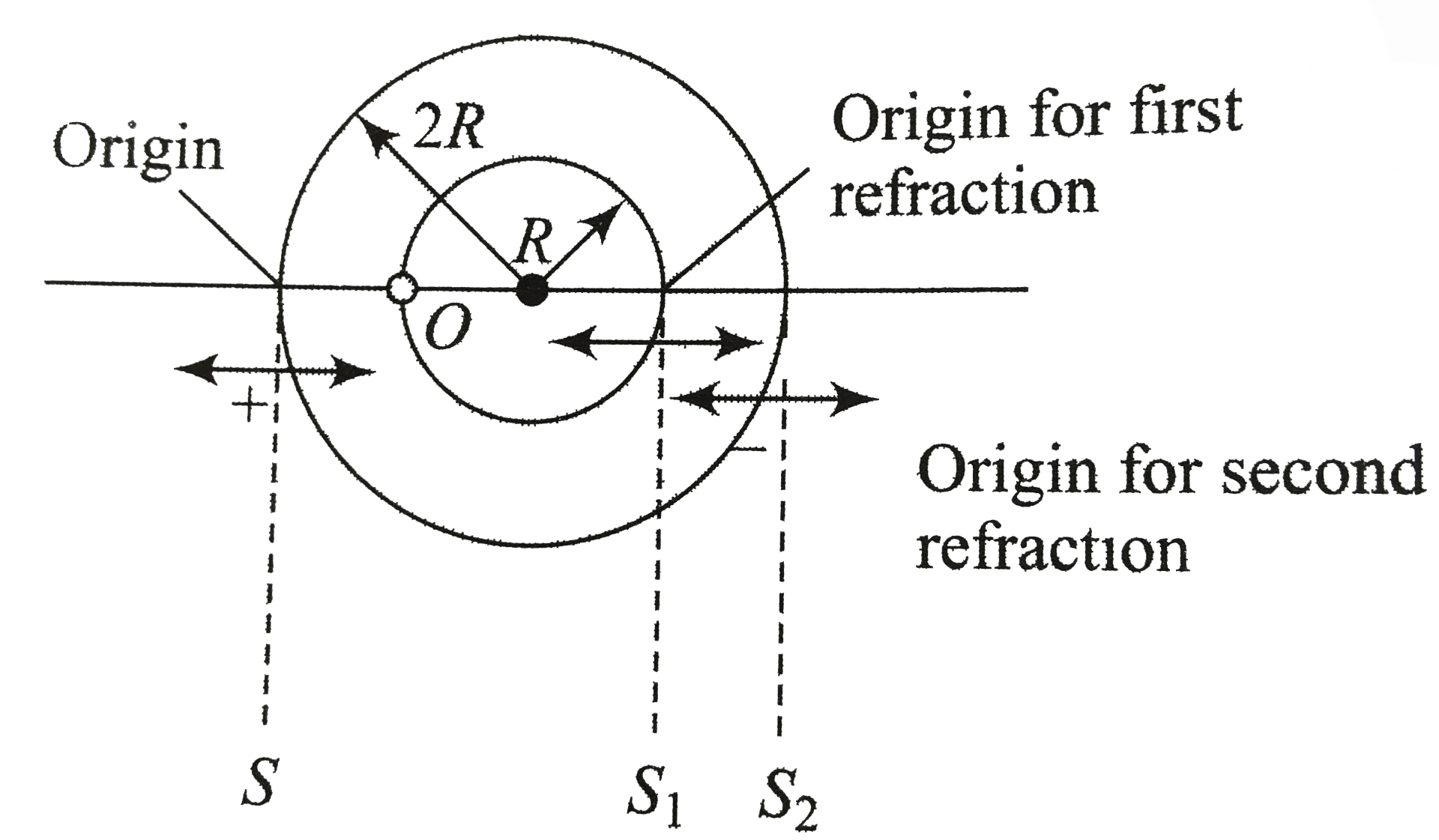
a. Viewer on the left of hollow sphere: Single refraction takes place at surface S.
From the single surface refraction equation, we have
μ2=1,μ1=n,u=−R,andR=−2R
1v−n(−R)=(1−n)(−2R)
which on solving for v yields, v=−(2Rn+1)
Image is on the right of refracting surface S.
Shift= Real depth-Apparent depth
R−(2Rn+1)=(n−1)(n+1)R
b. When the viewer is on the right, two rerfractions take place at surfaces S1 and S2.
μ2=n,μ1=1,u=−2R,andR=−R
For refraction at surface S1:nv1−1(−2R)=(n−1)(−R)
which on solving for v1=−2nR2n−1 .
The first lies to the left of S1 and acts as object for refraction at the second surface. We have to shift the origin of cartesian coordinate system to the vertex of S2. The object distance for the second surface is
u2=−[2nr2n−1+R]=−(4n−12n−1)R
Here μ2=1,μ1=n,R=−2R
⇒1v2−n−[4n−12n−1]R=1−n−2R
On solving for v2 , we get v2=−2(4n−1)(3n−1)R
The minus sign shows that image is virtual and lies to the left of S2 .
Shift= Real depth-Apparent depth
=3R−2(4n−1)R(3n−1)
=(n−1)(3n−1)R

Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Solved Examples
15 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.1
14 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
Similar Questions
A glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is ono left side of the hollow sphere, what will be the shift in position of the object?
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.
Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?

View SolutionA glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.

View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre. The charge at the inner surface, outer surface are respectively.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA cubical block of glass, refractive index 1.5, has a spherical cavity of radius r=9cm inside it as shown in figure . A luminous point object O is at a distance of 18cm from the cube. What is the apparent position of O as seen from A?
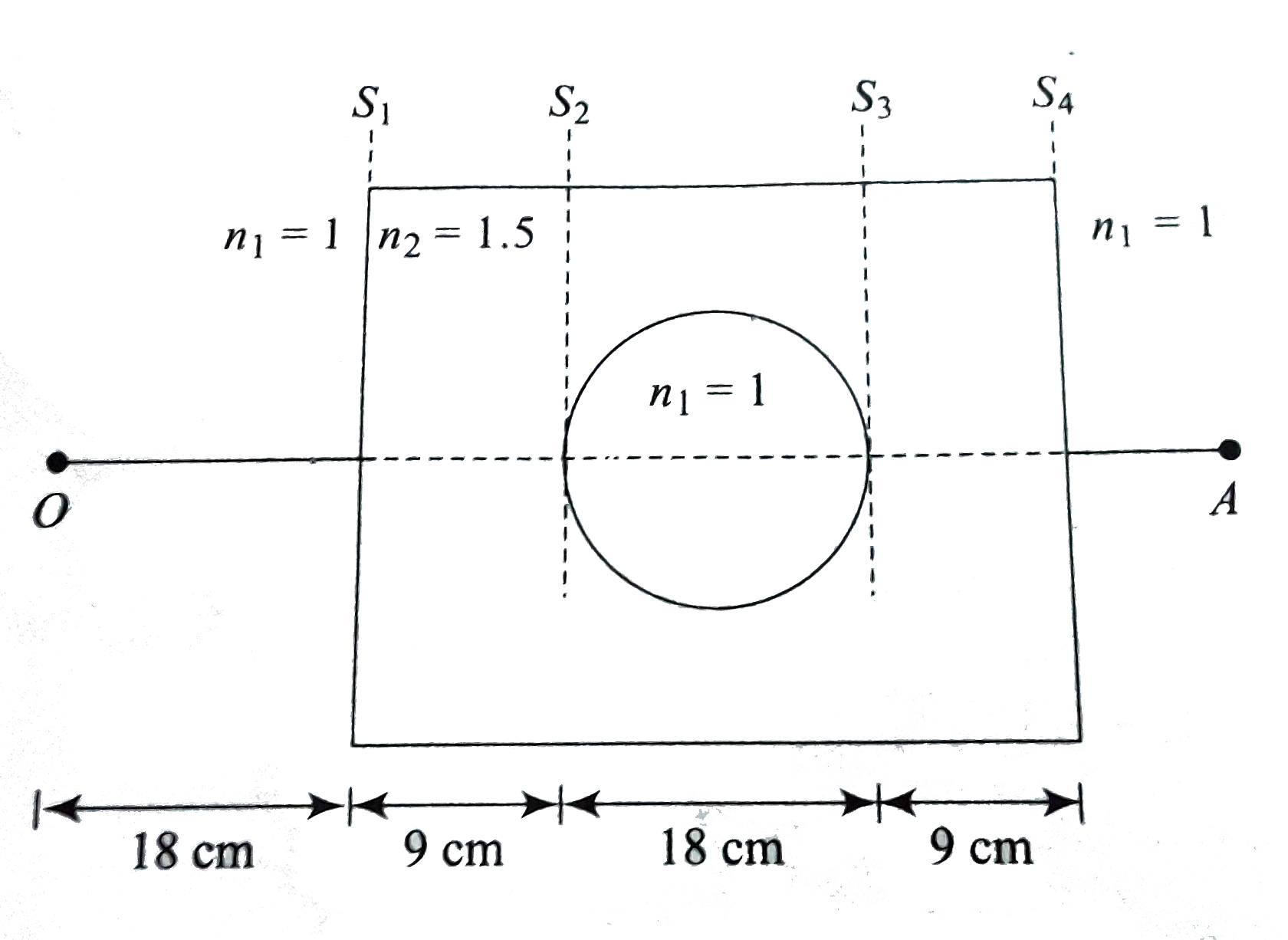
View SolutionA small object stuck on the surface of a glass sphere (n=1.5) is viewed from the diametrically opposite position. Find transverse magnification.
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
If q1 is shifted to the centre of the cavity, then: (choose the correct alternative)
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :
View Solution
