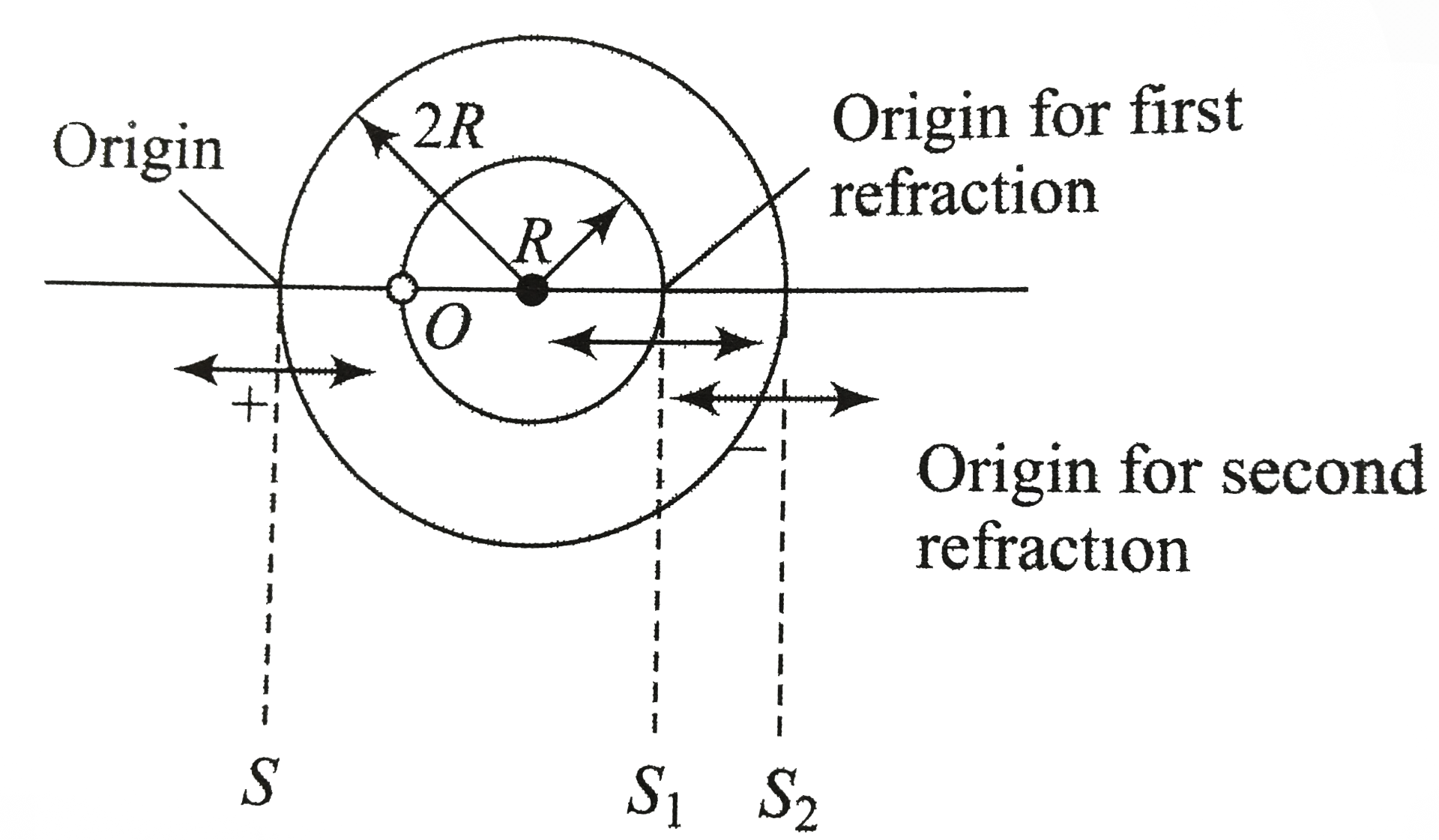
A glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.
Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?

(n−1)(3n+1)R,towards left
(n+1)(3n−1)R,towards left
(n+1)(3n+1)R,towards right
(n−1)(3n−1)R,towards right
The correct Answer is:b
(i) Viewer on the left of hollow sphere : Single refraction takes place at surface S. From the single surface refraction equation, we have
1v−n(−R)=(1−n)(−2R)
which on solving for v yields
v=−(2Rn+1)
Image is on the right of refracting surface S.
Shift = Real depth − Apparent depth
=R−(2Rn+1)=(n−1)(n+1)R
(ii) When the viewer is on the right, two refractions take place at surface S1 and S2.
For refraction at surface S1:
nv1−1(−2R)=(n−1)(−R)
which ono solving for v1 yields
v1=−2nR2n−1
The first lies to the left of S1 act as object for refraction at the second surface. We have to shift the origin of Cartesian coordinate system to the vertex of S2. The object distance for the second surface is
u2=−[2nR2n−1+R]=−(4n−12n−1)R
1v2=−n[4n−12n−1]=1−n−2R
On solving for v2 , we get
v2=−2(4n−1)3(n−1)R
The minus sign shows that image is virtual and lies to the left of S2.
Shift = Real depth − Apparent depth
=3R−2(4n−1)R(3n−1)=(n−1)(3n−1)R
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer15videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Archives7videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig2videos
GEOMETRICAL OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.315videos
ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
Similar Questions
A glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is ono left side of the hollow sphere, what will be the shift in position of the object?View SolutionA glass shere of radius 2R, refractive index n has a spherical cavity of radius R, concentric with it. A black spot on the inner surface of the hollow sphere is viewed from the left as well as right. Obtain the shift in position of the object.
 View Solution
View SolutionA glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.
 View Solution
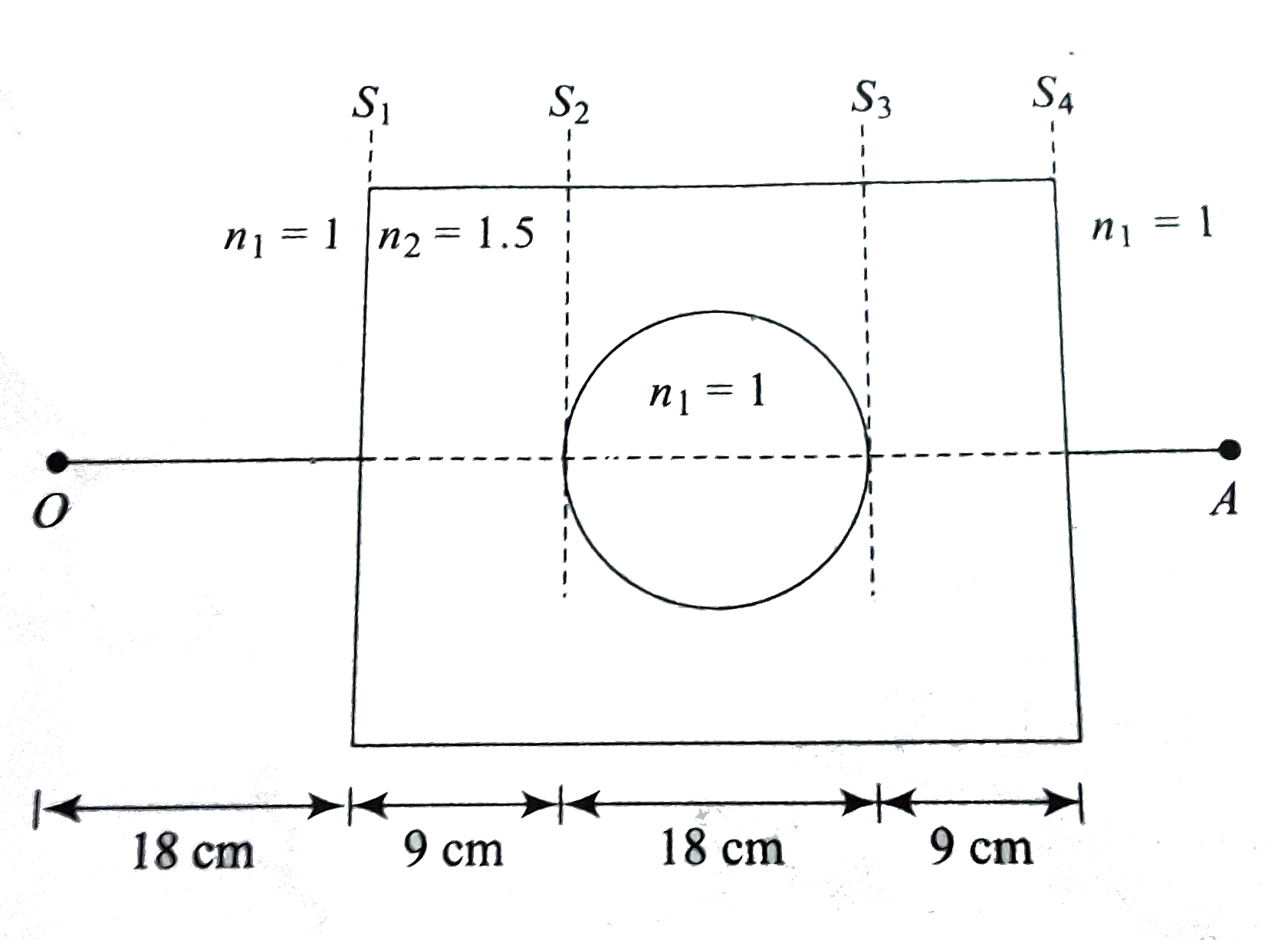
View SolutionA cubical block of glass, refractive index 1.5, has a spherical cavity of radius r=9cm inside it as shown in figure . A luminous point object O is at a distance of 18cm from the cube. What is the apparent position of O as seen from A?
 View Solution
View SolutionA sphere of radius R and charge Q is placed inside an imaginary sphere of radius 2R whose centre coincides with the given sphere. The flux related to imaginary sphere is:
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View SolutionA conducting sphere of radius r has a charge . Then .
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
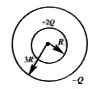
What would be the final distribution of charges if the sphres are joined by a conducting wireView SolutionA sphere of radius R has a uniform volume density ρ. A spherical cavity of radius b, whose center lies at →a, is removed from the sphere.
i. Find the electric field at any point inside the spherical cavity.
ii. Find the electric field outside the cavity
(a) at points inside the large sphere but outside the cavity and
(b) at points outside the large sphere.
 View Solution
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.

What would be the final distribution of charges if the sphres are joined by a conducting wireView Solution

