A glass sphere has radius of and a refractive index of A paperweight is constructed by slicing through the sphere on a plate that is from the centre of the sphere and perpendicular to radius of the sphere that passes through the centre of the circle formed by the intersection of the plane and the sphere. The paperweight is placed on a table and viewed from directly above an observer who is from the table top, as shown in figure. When viewed through the paperweight, how far away does the table top appear to the observer?
The correct Answer is:B, C, D
Applying we have,
Solving we get,
This is distance from P (downwards).
Distance from observer
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Subjective Questions
Explore 8 Videos
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Level 2 Single Correct
Explore 41 Videos
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Objective Questions
Explore 1 Video
- REFLECTION OF LIGHTBook:DC PANDEYChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEYChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
If a sphere of radius 10 cm is intersected by a plane at a distance 8 cm from its centre, what is the radius of the curve of intersection of the plane and the sphere?
View SolutionFind the equation of sphere which passes through (1,0,0) and has its centre on the positive direction of Y-axis and has radius 2.
View Solution
Knowledge Check
The potential of a sphere conductor of radius 5 cm is 10 V. what is the potential at the centre of the sphere?
A2 VB10 VCzeroD50 VA spherical cavity is made in a lead sphere of radius R such that its surface touches the outsides surface of lead sphere and passes through the centre. The shift in the centre of mass of the lead sphere as a result of this following, is
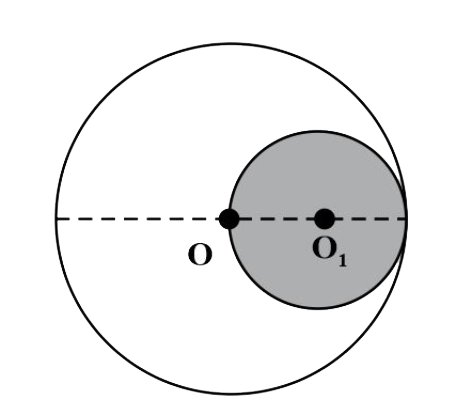 AR7BR14CR2DR
AR7BR14CR2DRAn electric dipole is placed at the centre of a sphere. Find the electric flux passing through the sphere.
A0B1C2DNone of the above
A glass sphere (μ=1.5) of radius 8 cm is placed in sunlight. Where is the image of the sun formed by the light passing through the sphere after refraction by second surface of sphere ?
View SolutionA positive charge of 17.7μC is placed at the centre of a hollow sphere of radius 0.5m. Calculate the flux density through the surface of the sphere.
View SolutionA glass sphere of diameter 20 cm is constructed with a material of refractive index 1.5. A beam of light strikes the sphere and converges at a point 40 cm behind the pole of a spherical surface. Find the position of the image.
View SolutionFlux passing through the shaded surface of a sphere when a point charge q is placed at the center is (radius of the sphere is R)
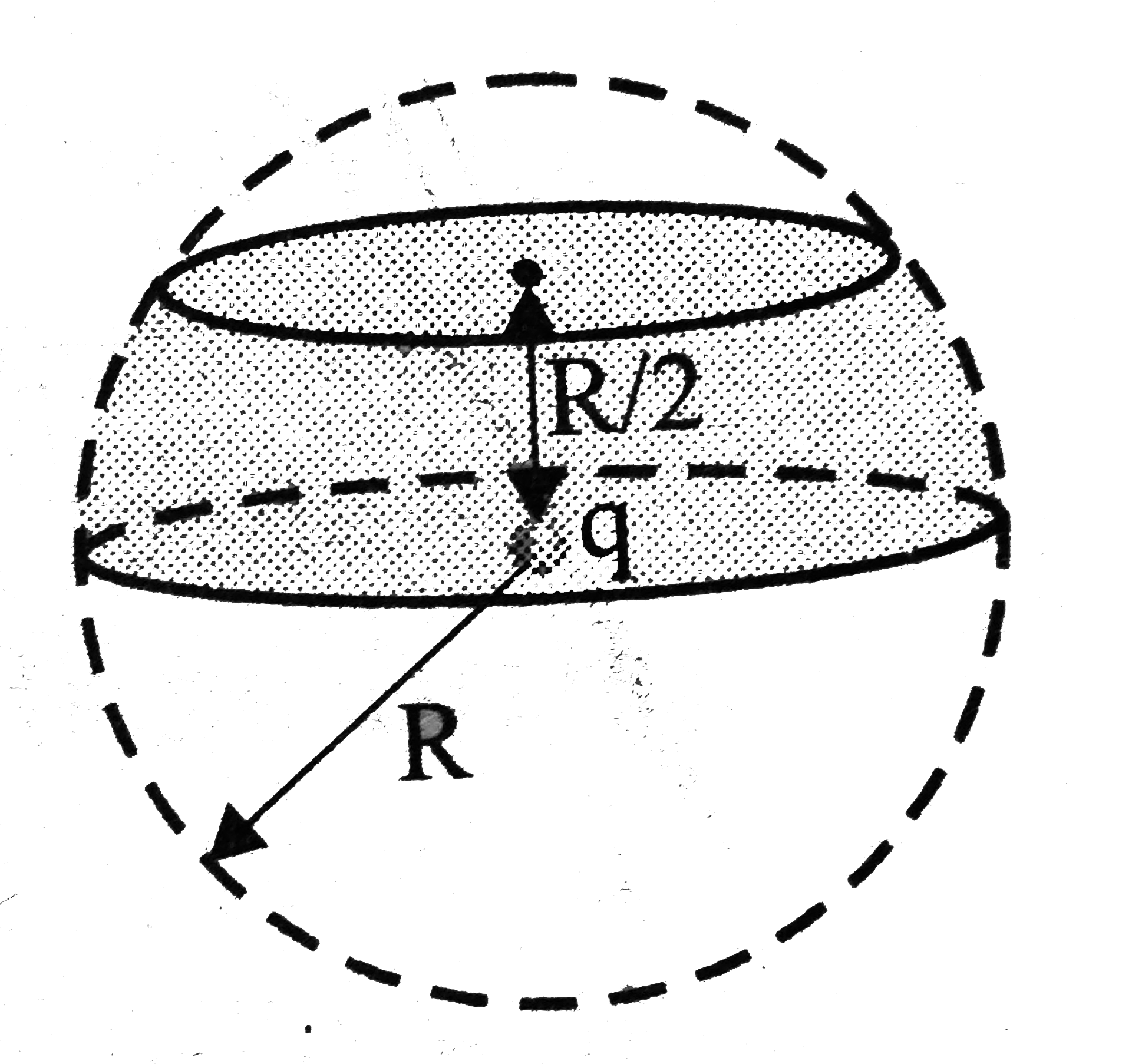
View SolutionA sphere has the same curved surface area as a cone of height 40 cm and radius 30 cm. The radius of the sphere is
View Solution