A glass sphere (μ=1.5) of radius 8 cm is placed in sunlight. Where is the image of the sun formed by the light passing through the sphere after refraction by second surface of sphere ?
4 cm
6cm
15cm
50 cm
To solve the problem of finding the image of the sun formed by a glass sphere with a refractive index of μ=1.5 and a radius of 8 cm, we can follow these steps:
Step 1: Understand the Setup
The sun is a very distant object, so we can consider the rays of sunlight entering the sphere to be parallel.
Step 2: Refraction at the First Surface
When the parallel rays of sunlight enter the sphere, they will refract at the first surface. We can use the lens maker's formula for refraction:
μ2V−μ1U=μ2−μ1R
Where:
- μ1=1 (refractive index of air)
- μ2=1.5 (refractive index of glass)
- U=∞ (the object distance for the sun)
- R=+8 cm (the radius of the sphere, taken as positive since it is convex)
Substituting the values:
1.5V−1∞=1.5−18
Since 1∞=0, we simplify this to:
1.5V=0.58
Step 3: Solve for V
Cross-multiplying gives:
1.5⋅8=0.5⋅V
12=0.5V
V=120.5=24 cm
This means the image I1 is formed 24 cm from the center of the sphere on the opposite side.
Step 4: Refraction at the Second Surface
Now, this image I1 acts as the object for the second surface of the sphere. The object distance U for the second surface is:
U=−(24−8)=−16 cm
(Note: The distance is negative because the object is on the same side as the incoming light.)
Using the same formula for the second surface:
μ2V2−μ1U=μ2−μ1R
Where:
- R=−8 cm (the radius of the second surface, taken as negative since it is concave from the perspective of the incoming light)
Substituting the values:
1.5V2−1−16=1.5−1−8
This simplifies to:
1.5V2+116=0.5−8
Step 5: Solve for V2
Now, we can rewrite this as:
1.5V2+116=−0.0625
To isolate V2, we first convert −0.0625 to a fraction:
1.5V2=−0.0625−116
Finding a common denominator (16):
−0.0625=−116
Thus:
1.5V2=−1+116=−216=−18
Cross-multiplying gives:
1.5⋅8=−V2
12=−V2⟹V2=−12 cm
Conclusion
The image of the sun formed by the light passing through the sphere after refraction by the second surface is located at 4 cm from the center of the sphere on the opposite side.
Final Answer
The image of the sun is formed at a distance of 4 cm from the center of the sphere.
---
The sun is a very distant object, so we can consider the rays of sunlight entering the sphere to be parallel.
When the parallel rays of sunlight enter the sphere, they will refract at the first surface. We can use the lens maker's formula for refraction:
- μ1=1 (refractive index of air)
- μ2=1.5 (refractive index of glass)
- U=∞ (the object distance for the sun)
- R=+8 cm (the radius of the sphere, taken as positive since it is convex)
Cross-multiplying gives:
Now, this image I1 acts as the object for the second surface of the sphere. The object distance U for the second surface is:
- R=−8 cm (the radius of the second surface, taken as negative since it is concave from the perspective of the incoming light)
Now, we can rewrite this as:
The image of the sun formed by the light passing through the sphere after refraction by the second surface is located at 4 cm from the center of the sphere on the opposite side.
The image of the sun is formed at a distance of 4 cm from the center of the sphere.
Topper's Solved these Questions
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Advance MCQs with One or More Options Correct30videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Unsolved Numerical Problems107videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Conceptual MCQs Single Option Correct43videos
GEOMETRICAL OPTICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems73videos
ELECTROSTATICS
- BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO82videos
HEAT AND THERMAL EXPANSION
Similar Questions
A small object is embedded in a glass sphere (μ−1.5) of radius 5.0cm left to the center. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.
View SolutionA small object is embedded in a glass sphere (mu =1.5) of radius 5.0 cm at a distance 1.5 cm left to the centre. Locate the image of the object as seen by an observer standing (a) to the left of the sphere and (b) to the right of the sphere.
View Solution
Knowledge Check
- Question 1 - Select One
There is a small air bubble inside a glass sphere (μ=1.5) of radius 5 cm. The bubble is 7.5 cm below the surface of the glass. The sphere is placed inside water (μ=43) such that the top surface of glass is 10 cm below the surface of water. The bubble is viewed normally from air. Find the apparent depth on the bubble.
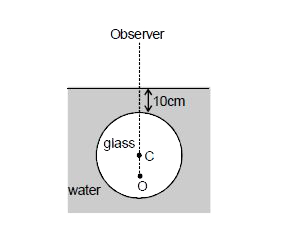 A15 cm below the surface of waterB10.5 cm below the surface of waterC16.66 cm below the surface of waterD13.5 cm below the surface of water
A15 cm below the surface of waterB10.5 cm below the surface of waterC16.66 cm below the surface of waterD13.5 cm below the surface of water - Question 2 - Select One
A glass sphere (μ =1.5) of radius 20 cm has small air bubble 4 cm below its centre. The sphere is viewed from outside and along vertical line through the bubble. The apparent depth of the bubble below the surface of sphere is (in cm)
A13.33B26.67C15D30 - Question 3 - Select One
A hollow metal sphere of radius 5 cms is charged such that the potential on its surface is 10 volts. The potential at the centre of the sphere is
A(a) zeroB(b) 10 voltsC(c) same as at a point 5 cms away from the surfaceD(d) same as at a point 25 cms away from the surface
A hemispherical portion of the surface of a solid glass sphere (mu = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
View SolutionThere is small air bubble inside a glass sphere (μ=1.5) of radius 5cm. The bubble is at 'O' at 7.5cm below the surface of the glass. The sphere is placed inside water (μ=43) such that the top surface of glass is 10cm below the surface of water. The bubble is viewed normally from air. Find the apperent depth of the bubble.
 View Solution
View SolutionRadius of a sphere is 14 cm. Find the surface area of the sphere.
View SolutionA conducting sphere of radius 10cm is charged 10μC. Another uncharged sphere of radius 20cm is allowed to touch it for some tome. After that if the sphere are separted, then surface density of chsrges, on the spheres will be in the ratio of
View SolutionThe radius of a sphere is 21cm, what is the surface area of the sphere?
View Solution

