A glass tube is open at both the ends. A tuning fork of
frequency f resonates with the air column inside the
tude. Now, the tube is placed bertically inside water
so that half the length of the tube is filled with water.
Now, the air column inside the tube is in unison with
another fork of frequency f . Then
f'=f
f'=4f
f'=2f
f'=f2
The correct Answer is:a
For fundamental frequency of vibration of air column
l=λ2⇒λ=2l
Frequency, f=vλ⇒f=v2l …(i)
When tube is placed inside water with half length
immersed in water, then

l=λ2 /2=λ24
l2=λ4⇒λ'=2l
Frequency f'=vλ'=v2l ...(ii)
From Eqs. (i) and (ii) we get f'=f
Topper's Solved these Questions
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - EXERCISE 2
27 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- SEMICONDUCTORSBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SEMICONDUCTORSEXERCISE - MHT CET Corner
25 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
Similar Questions
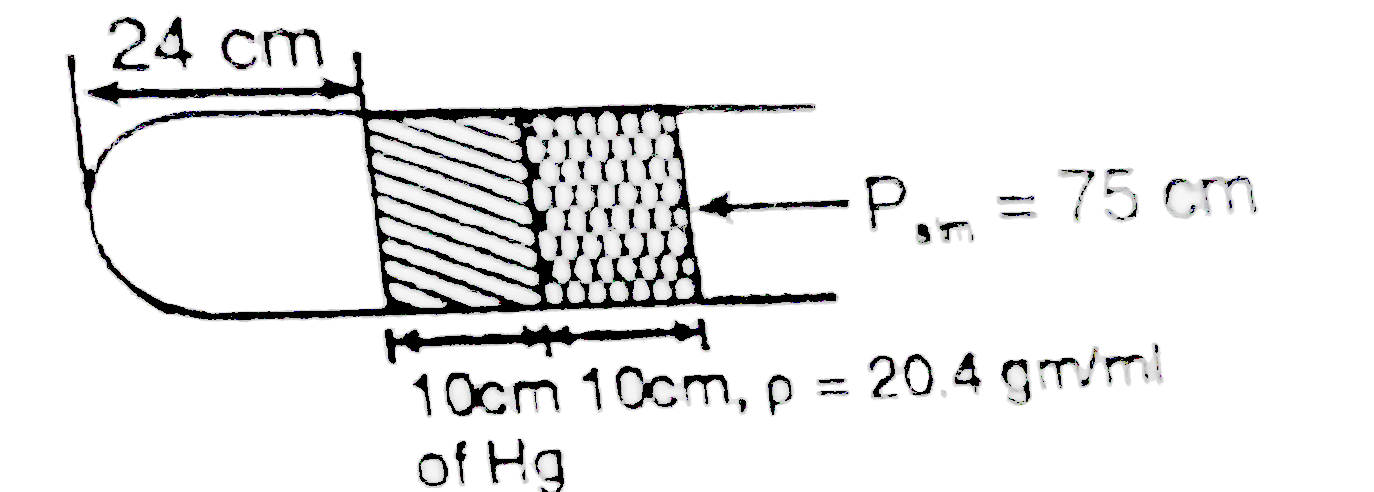
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionA cylinderical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air column is now
View Solution
Knowledge Check
A cylindrical tube open at both ends, has a fundamental frequency 'f in air. The tube is dipped vertically in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column in now
Af2B3f4CfD2fA cylindrical tube, open at the both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of it is in water . The fundamental frequency of the air column is now-
Af/2B3f/4CfD2fA cylindrical tube, open at the both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of it is in water . The fundamental frequency of the air column is now-
Af/2B4C3f/4D2f
A cylindrical tube, open at both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of its length is in water. The fundamental frequency of the air column is now
(a) f/2
(b) 3f/4
(C ) f
(d) 2f
View SolutionA cylindrical tube open at both the ends has a fundamental frequency of 390 Hz in air. If 14 th of the tube is immesed vertically in water the fundamental frequency of air column is
View SolutionA tuning fork of frequency n is held near the open end of tube, the tube is adjusted until resonance occurs. If the two shortest lengths to produce resonance are L1andL2 , then the speed of the sound is
View SolutionA cylindrical tube open at both ends, has a fundamental frequency F in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air column is now
View SolutionA cylindrical tube open at both ends, has a fundamental frequency F in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air column is now
View Solution
