A glass tube of uniform internal radius r has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r.
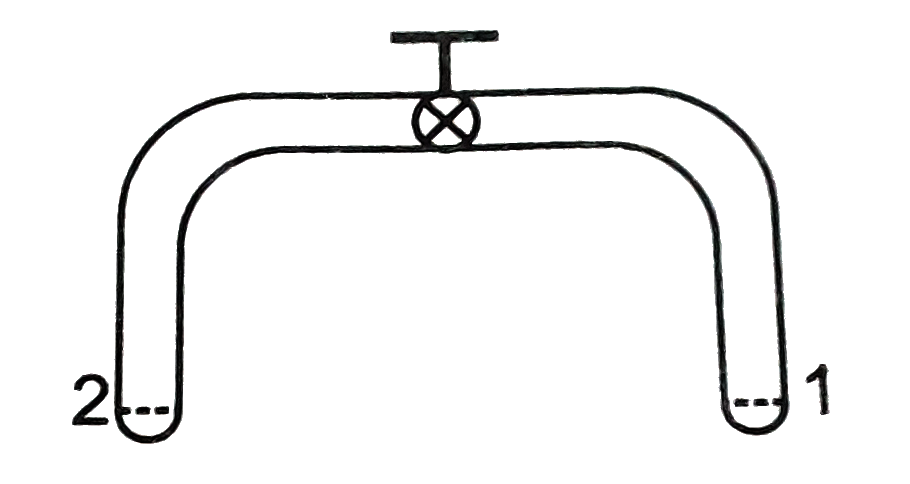
End 2 has sub-hemispherical soap bubble as shown in the figure. Just after opening the valve,
air from End 1 flows towards End 2. No change in the volume of the soap bubbles
air from End 1 flows towards End 2. Volume of the soap bubble at End 1 decreases
air from End 2 flows towards End 1. Volume of the soap bubble at End 1 increases
no change occurs
The correct Answer is:D
and
Since
So no change occurs
Topper's Solved these Questions
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - Exercise 2 (Miscellaneous Problems)
42 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- WAVE MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE MOTIONEXERCISE - MHT CET CORNER
23 Videos
Similar Questions
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.

View SolutionA glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
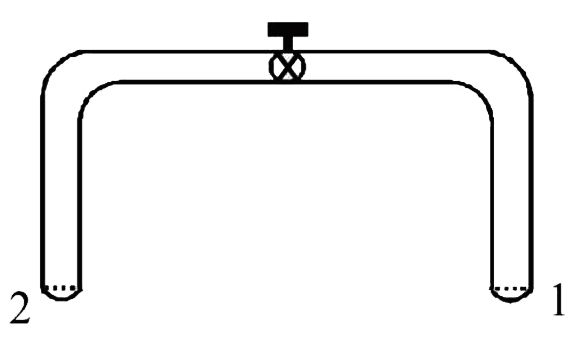
View Solution
Knowledge Check
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve.
 Aair from end 1 flows towards 2. No change in the volume of the soap bubblesBair from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesCno change occursDair form end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.
Aair from end 1 flows towards 2. No change in the volume of the soap bubblesBair from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesCno change occursDair form end 2 flows towards end 1. Volume of the soap bubble at end 1 increases.A glass tube of uniform internal radius(r) has a valve separating the two identical ends. Intially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble or radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
 A(a) air from end 1 flows towards end 2. No change in the volume of the soap bubblesB(b) air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesC(c) no changes occursD(d) air from end 2 flows towards end 1. volume of the soap bubble at end 1 increases
A(a) air from end 1 flows towards end 2. No change in the volume of the soap bubblesB(b) air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreasesC(c) no changes occursD(d) air from end 2 flows towards end 1. volume of the soap bubble at end 1 increasesTwo spherical soap bubbles of radii r1 and r2 in vacuume collapse under isothermal condition. The resulting bubble has radius R such that
AR=r1+r2BR=(r1+r2)12CR=√r21+r22DR=[(r2r2(r1+r2)]
Two soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
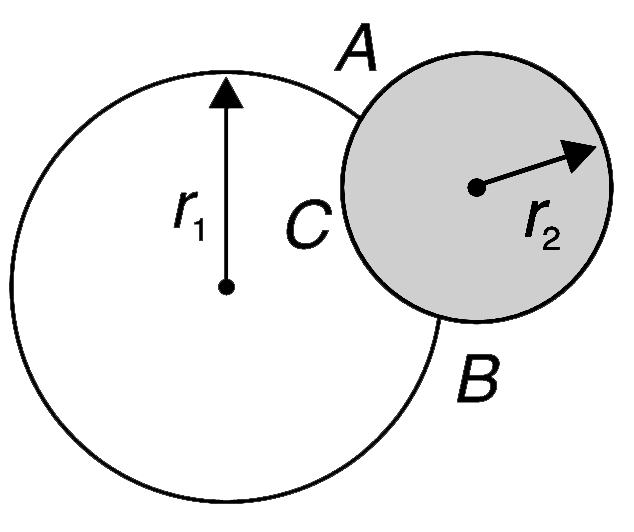
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.

View SolutionTwo soap bubbles with radius 2r and 3r come in contact. Their common surface has a radius of curvature nr, then find the value of n
View SolutionTwo soap bubbles of radius R1 and R2 combine isothermally to form a new soap bubble. Find radius of new soap bubble
View SolutionTwo spherical soap bubbles of a radii 1 cm and 2 cm vacuum coalesce under isothermal conditions . The resultant bubble has a radius of
View Solution
