When two soap bubbles of radius r1 and r2(r2>r1) coalesce, the radius of curvature of common surface is
(r2−r1)
(r2+r1)
r2−r1r1r2
r1r2r2−r1
The correct Answer is:D
The excess pressure inside the first bubble of radius r1 is p1=4S/r1 and in the second bubble of radius r2 is p2=4S/r2.
∴ Excess pressure, p=4Sr=4Sr1−4Sr2

⇒1r=r2−r1r1r2⇒r=r1r2r2−r1
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - Exercise 2 (Miscellaneous Problems)42videos
SURFACE TENSION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner15videos
SURFACE TENSION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner15videos
SURFACE TENSION
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner28videos
STATIONARY WAVES
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE MOTIONEXERCISE - MHT CET CORNER23videos
WAVE MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Two soap bubbles each of radius r are touching each other. The radius of curvature of the common surface will be:
AinfiniteB2rCrDr/2 - Question 2 - Select One
If two bubble of radii 0.03 cm and 0.04 cm come in contact with each other then the radius of curvature of the common surface 'r' is given by.
A0.03B0.06C0.12D0.24 - Question 3 - Select One
A soap bubble of radius r1 is placed on another soap bubble of radius r2(r1<r2). The radius R of the soapy film separating the two bubbles is :
Ar1+r2B√r21+r22C(r31+r32)Dr2r1r2−r1
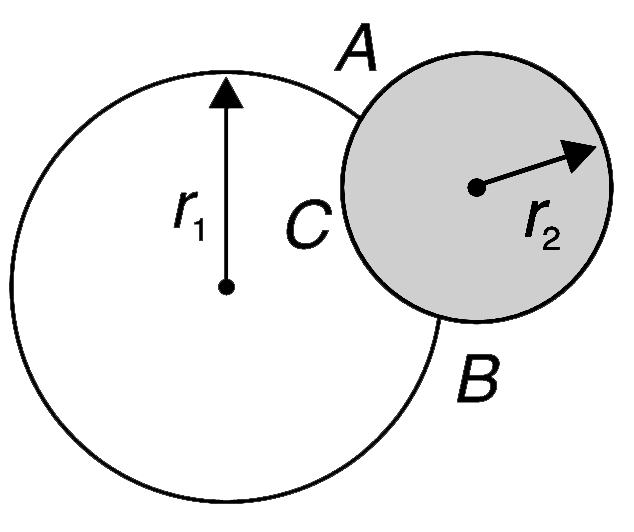
Two soap bubbles of radii r1andr2 are attached as shown. Find the radius of curvature of the common film ACB.
 View Solution
View SolutionProve that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
View SolutionUnder isothermal condition two soap bubbles of radii r1 and r2 coalesce to form a single bubble of radius r. The external pressure is p0. Find the surface tension of the soap in terms of the given parameters.
View SolutionTwo soap bubble of radius 2r and 3r are in contact with each other. If the radius of curvature of the interface between the bubble in nr then find the value of n:
View SolutionIf two soap bubbles of equal radii r coalesce then the radius of curvature of interface between two bubbles will be
View Solution


