A harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
frequency of wave may change
wave speed may change
both frequency and speed of wave may change
only frequency will change
The correct Answer is:a., b., c.,d.
To solve the problem, we need to understand the relationship between wavelength (λ), frequency (f), and wave velocity (v). The fundamental wave equation that relates these three quantities is:
v=f⋅λ
Where:
- v is the wave velocity,
- f is the frequency,
- λ is the wavelength.
Now, let's analyze the situation step by step.
Step 1: Understand the Initial Conditions
Assume the initial wavelength is λ1 and the initial frequency is f1. The initial wave velocity can be expressed as:
v1=f1⋅λ1
Step 2: Doubling the Wavelength
According to the problem, the wavelength is doubled. Therefore, the new wavelength λ2 can be expressed as:
λ2=2⋅λ1
Step 3: Analyze the Wave Velocity
If the medium remains unchanged, the wave velocity v is determined by the properties of the medium. For a stretched string, the wave velocity is constant and depends on the tension and mass per unit length of the string. Thus, we can say:
v2=v1
Step 4: Relate Frequency and Wavelength
Using the wave equation for the new conditions, we can express the new frequency f2:
v2=f2⋅λ2
Since we established that v2=v1, we can substitute:
v1=f2⋅(2⋅λ1)
Step 5: Solve for the New Frequency
We can rearrange this equation to find the new frequency f2:
f2=v12⋅λ1
Since we know that v1=f1⋅λ1, we can substitute v1:
f2=f1⋅λ12⋅λ1
This simplifies to:
f2=f12
Conclusion
In conclusion, when the wavelength of the wave is doubled:
- The wave velocity remains constant (v2=v1).
- The frequency is halved (f2=f12).
- v is the wave velocity,
- f is the frequency,
- λ is the wavelength.
Assume the initial wavelength is λ1 and the initial frequency is f1. The initial wave velocity can be expressed as:
According to the problem, the wavelength is doubled. Therefore, the new wavelength λ2 can be expressed as:
If the medium remains unchanged, the wave velocity v is determined by the properties of the medium. For a stretched string, the wave velocity is constant and depends on the tension and mass per unit length of the string. Thus, we can say:
Using the wave equation for the new conditions, we can express the new frequency f2:
We can rearrange this equation to find the new frequency f2:
In conclusion, when the wavelength of the wave is doubled:
- The wave velocity remains constant (v2=v1).
- The frequency is halved (f2=f12).
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Assertion-Reasoning6videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Comprehension45videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer1videos
TRAVELLING WAVES
- BOOK - CENGAGE PHYSICSCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct9videos
TRANSMISSION OF HEAT
- BOOK - CENGAGE PHYSICSCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct5videos
VECTORS
Similar Questions
The figure represents the instantaneous picture of a longitudinal harmonic wave travelling along the negative x-axis. Identify the correct statement related to the movement of the points shown in the figure.
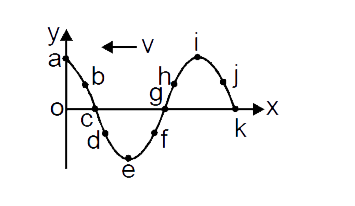
The points moving in the direction of wave areView SolutionA harmonic wave travelling in a medium has a period T and wavelength X. How far does the wave travel in time T ?
View Solution
Knowledge Check
- Question 1 - Select One
The speed of transverse wave on a stretched string is
Adirectly proportional to the tension in the stringBdirectly proportional to the square root of the tensionCinversely proportional to liveDinversely proportional to square of tension - Question 2 - Select One or More
transverse simple harmonic wave is travelling on a string. The equation of the wave:
AIs the general equation for displacement of a particle of the string at any instant tBIs the equation ofthe shape ofthe string at any instant tCMust have sinusoidal formDIs an equation ofdisplacement for the particle at any one end at a particular time t - Question 3 - Select One or More
y−x curve at an instant for a wave travelling along x−axis on a string is shown. Slope at the point A on the curve, as shown, is tan53∘.
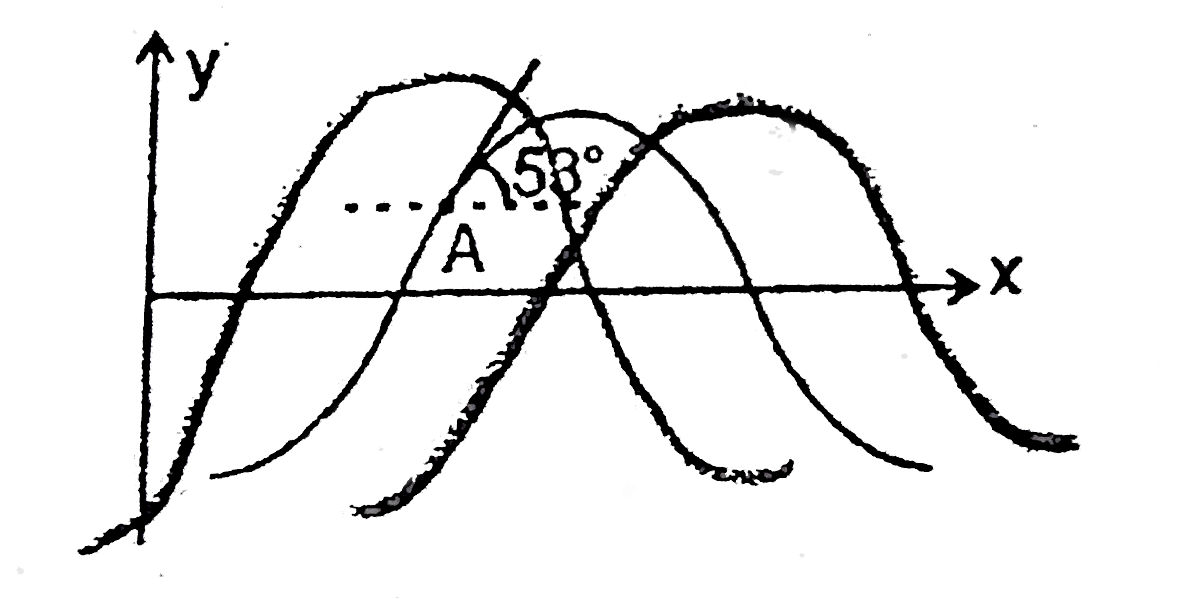 ATransverse velocity of the particle at point A is positive if the wave is travelling along positive x−axis.BTransverse velocity of the particle at point A is positive if the wave is travelling along negative x−axis of the particle at point ACMagnitude of transverse velocity of the particle at point A is greater than wave speed.DMagnitude of transverse velocity of the particle at point A is lesser than wave speed.
ATransverse velocity of the particle at point A is positive if the wave is travelling along positive x−axis.BTransverse velocity of the particle at point A is positive if the wave is travelling along negative x−axis of the particle at point ACMagnitude of transverse velocity of the particle at point A is greater than wave speed.DMagnitude of transverse velocity of the particle at point A is lesser than wave speed.
A harmonic wave travelling in a medium has a period T and wavelength X. How are X and T related ?
View SolutionStationary waves
View SolutionTwo waves are travelling in same direction along a stretched string. The waves are 90∘ out of phase. Each wave has an amplitude of 4.0 cm. Find the amplitude of the resultant wave.
View SolutionThe velocity of wave in a stretched string is proportional to
View SolutionLight waves travel in vacuum along the y-axis. Which of the following may represent the wavefront?
View Solution

