A harmonic wave is travelling in a stationary medium whose equation of this wave w.r.t. a frame which is moving along -ve x-axis with a constant speed v w.r.t. stationary medium. Also, find speed of wave in moving frame.
To solve the problem step by step, we will analyze the situation involving two frames of reference: a stationary medium and a moving frame.
Step 1: Understand the Problem
We have a harmonic wave traveling in a stationary medium. We need to find the equation of this wave in a frame that is moving along the negative x-axis with a constant speed v.
Step 2: Write the Wave Equation in the Stationary Frame
The wave equation in the stationary medium can be expressed as:
y(x,t)=Asin(kx−ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency.
Step 3: Determine the Speed of the Wave in the Stationary Medium
The speed of the wave Vw in the stationary medium is given by:
Vw=√Tμ
where:
- T is the tension in the medium,
- μ is the linear mass density.
Step 4: Analyze the Moving Frame
Now, we consider a frame (Frame 2) that is moving with a speed v along the negative x-axis. To analyze the wave in this moving frame, we need to adjust the wave equation to account for the motion of the frame.
Step 5: Adjust the Wave Equation for the Moving Frame
In the moving frame, the wave will appear to travel at a different speed. The relationship between the wave speed in the stationary frame and the moving frame can be expressed as:
Vwave,moving=Vwave,stationary+v
Since the moving frame is moving in the negative x-direction, we need to consider the direction of the wave speed as well.
Step 6: Write the Equation for the Speed of the Wave in the Moving Frame
Thus, we can write:
Vwave,moving=√Tμ+v
Step 7: Final Expression
The speed of the wave in the moving frame (Frame 2) is:
Vwave,moving=√Tμ+v
Summary of the Solution
The speed of the wave in the moving frame is the sum of the wave speed in the stationary medium and the speed of the moving frame.
We have a harmonic wave traveling in a stationary medium. We need to find the equation of this wave in a frame that is moving along the negative x-axis with a constant speed v.
The wave equation in the stationary medium can be expressed as:
y(x,t)=Asin(kx−ωt)
where:
- A is the amplitude,
- k is the wave number,
- ω is the angular frequency.
The speed of the wave Vw in the stationary medium is given by:
Vw=√Tμ
where:
- T is the tension in the medium,
- μ is the linear mass density.
Now, we consider a frame (Frame 2) that is moving with a speed v along the negative x-axis. To analyze the wave in this moving frame, we need to adjust the wave equation to account for the motion of the frame.
In the moving frame, the wave will appear to travel at a different speed. The relationship between the wave speed in the stationary frame and the moving frame can be expressed as:
Vwave,moving=Vwave,stationary+v
Since the moving frame is moving in the negative x-direction, we need to consider the direction of the wave speed as well.
Thus, we can write:
Vwave,moving=√Tμ+v
The speed of the wave in the moving frame (Frame 2) is:
Vwave,moving=√Tμ+v
The speed of the wave in the moving frame is the sum of the wave speed in the stationary medium and the speed of the moving frame.
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.2
23 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A harmonic wave is travelling along +ve x-axis, on a stretched string. If wavelength of the wave gets doubled, then
View Solutionin a sine wave ,postive of different particles at time t=0 is shown in figure. The equation for this wave if it is travelling along postive x -axis can beB
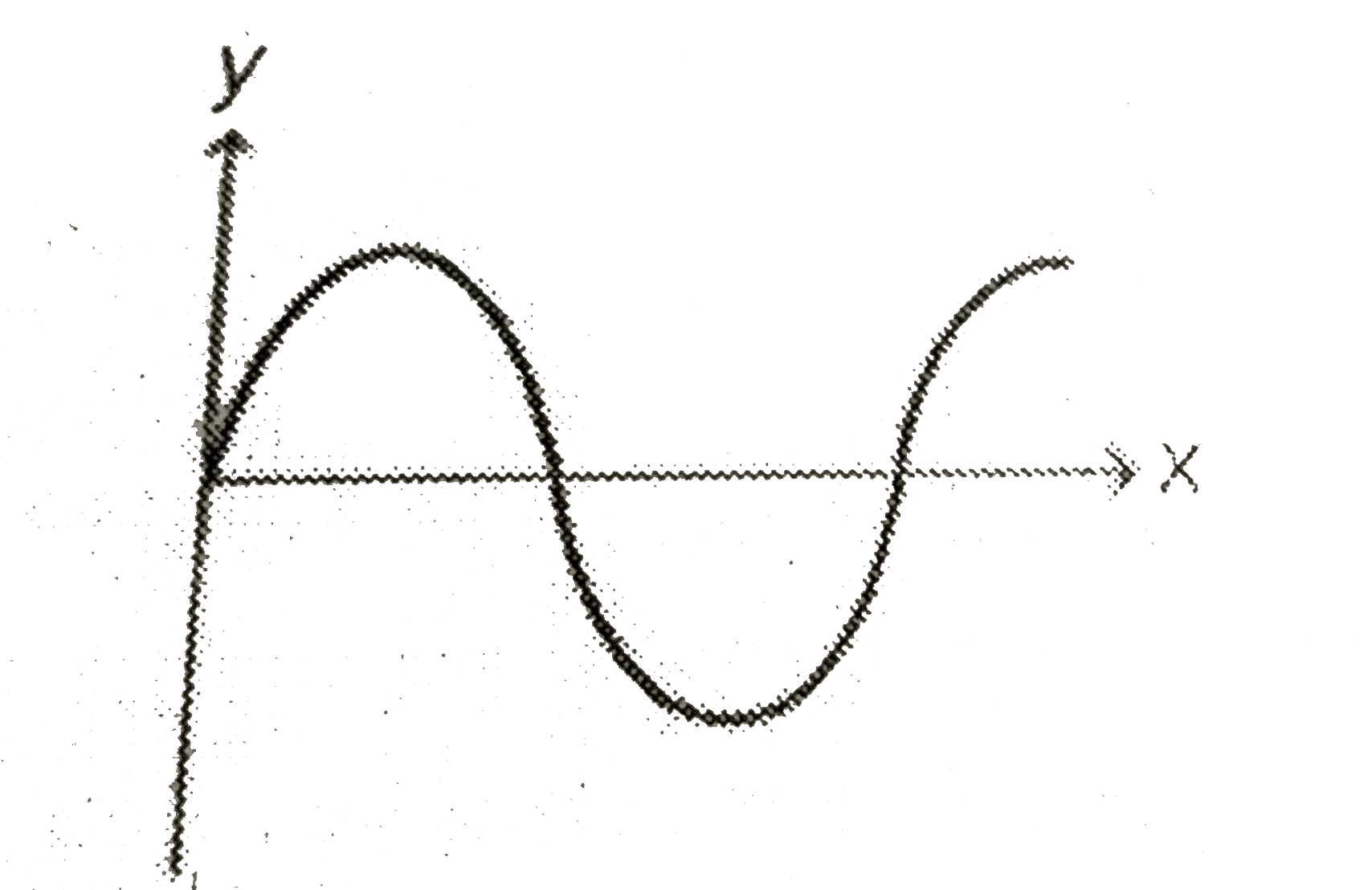
View Solutionthe equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by

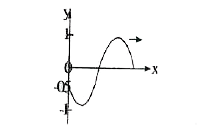
View SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t = 0 is given by
View SolutionA transverse wave travels along x-axis . The particles of medium move
View SolutionA plane sound wave is travelling in a medium. In reference to a frame A, its equation is y=a cos (ωt−kx). Which refrence to frame B, moving with a constant velocity v in the direction of propagation of the wave, equation of the wave will be
View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionA transverse wave travels along the Z-axis. The particles of the medium must move
View SolutionThe position of a transverse wave travelling in medium along positive x-axis is shown in figure at time t=0. Speed of wave is v=200 m/s
Frequency of the wave is

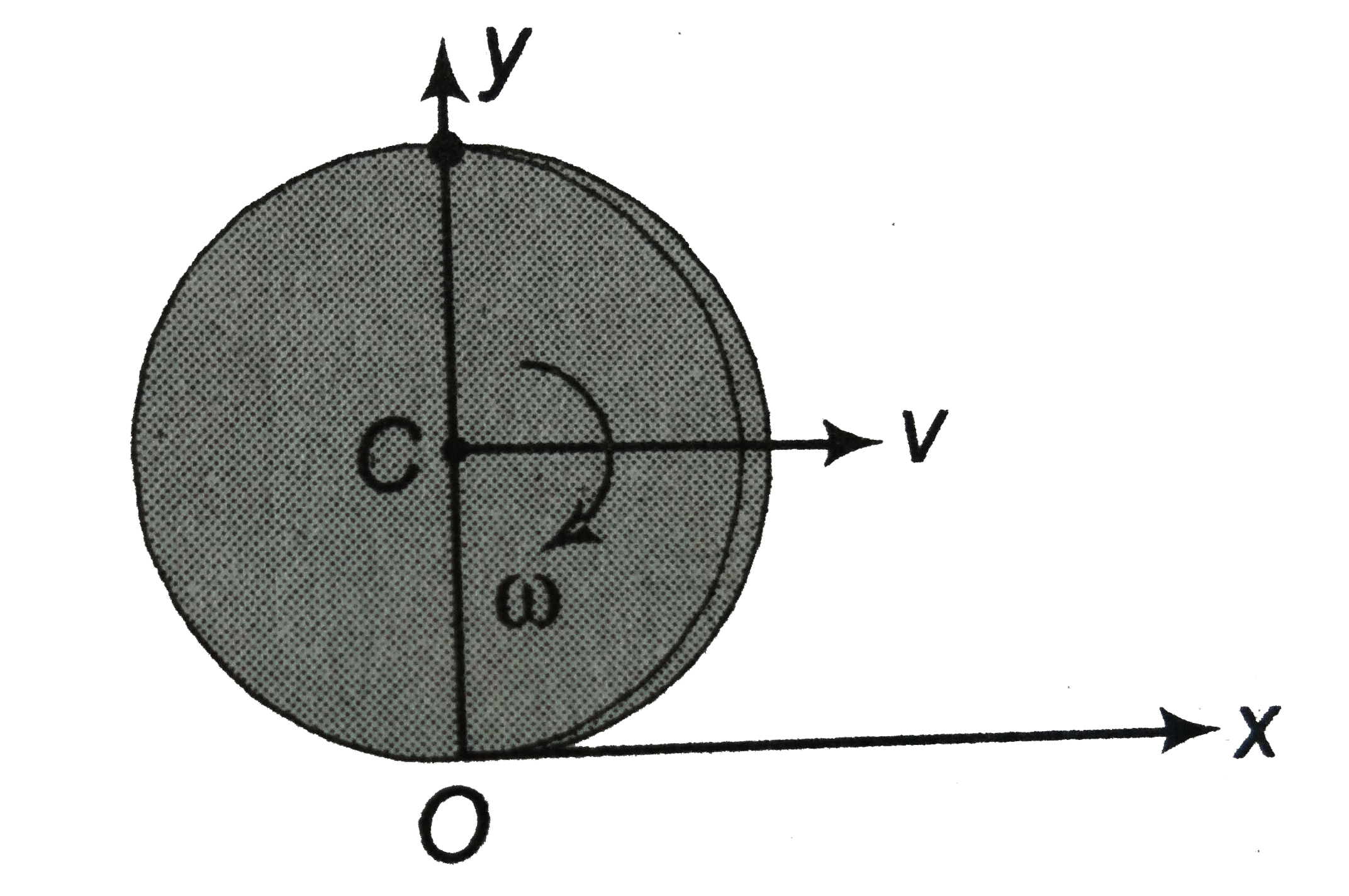
View SolutionA disc of radius R starts at time t=0 moving along the positive x-axis with linear speed v and angular speed ω. Find the x and y coordinates of the bottom most poitn at any time t.
View Solution
