A transverse wave travels along the Z-axis. The particles of the medium must move
along the Z-axis
along the X-axis
along the Y-axis
in the XY-plane
The correct Answer is:D
To solve the question regarding the motion of particles in a transverse wave traveling along the Z-axis, we can follow these steps:
1. Understand the Definition of a Transverse Wave:
- A transverse wave is characterized by the movement of particles in a direction that is perpendicular to the direction of wave propagation.
2. Identify the Direction of Wave Propagation:
- In this case, the wave is traveling along the Z-axis.
3. Determine the Direction of Particle Motion:
- Since the particles of the medium move perpendicular to the direction of wave propagation (which is along the Z-axis), the motion of the particles will be in a plane that is perpendicular to the Z-axis.
4. Identify the Perpendicular Plane:
- The plane that is perpendicular to the Z-axis is the XY-plane. Therefore, the particles of the medium must move within this plane.
5. Select the Correct Option:
- From the options provided, the correct answer is that the particles of the medium must move in the XY-plane.
Final Answer:
The particles of the medium must move in the XY-plane.
---
- A transverse wave is characterized by the movement of particles in a direction that is perpendicular to the direction of wave propagation.
- In this case, the wave is traveling along the Z-axis.
- Since the particles of the medium move perpendicular to the direction of wave propagation (which is along the Z-axis), the motion of the particles will be in a plane that is perpendicular to the Z-axis.
- The plane that is perpendicular to the Z-axis is the XY-plane. Therefore, the particles of the medium must move within this plane.
- From the options provided, the correct answer is that the particles of the medium must move in the XY-plane.
The particles of the medium must move in the XY-plane.
Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises
57 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Question for short Answer
7 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -1
20 Videos
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer
9 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
Similar Questions
Knowledge Check
In a transverse wave, the particles of the medium
Avibrate in a direction perpendicular to the direction of the propagation.Bvibrate in a direction parallel to the direction or of the propagationCmove in circleDmove in ellipse
A transverse wave is travelling on a string. The equation of the wave
View SolutionIn a stationary wave system, all the particles of the medium
View SolutionA wave is propagating along x-axis. The displacement of particles of the medium in z-direction at t=0 is given by : z=exp[−(x+2)2] where 'x' is in meter. At t=1s, the same wave disturbance is given by z=exp[−(x−2)2]. Then the wave propagation velocity is :-
View SolutionThe figure represents the instantaneous picture of a transverse harmonic wave traveling along the negative x-axis. Choose the correct alternative(s) related to the movement of the nine points shown in the figure.

The points moving downwards is
View SolutionA transverse wave travelling along the positive x-axis, given by y=Asin(kx−ωt) is superposed with another wave travelling along the negative x-axis given by y=Asin(kx+ωt). The point x=0 is
View SolutionA transverse wave is travelling along a string in the positive x-axis. The
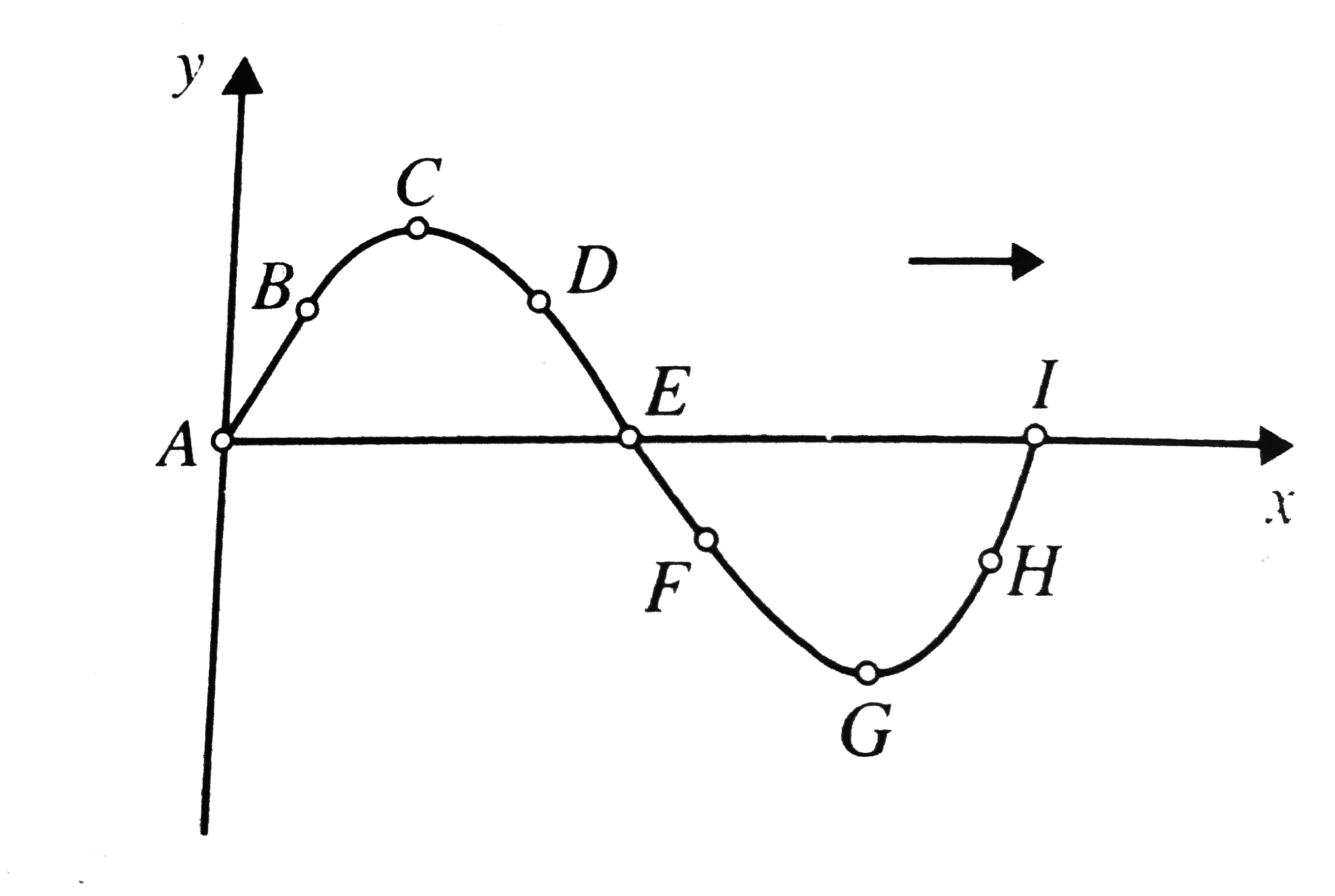
shows the photograph of the wave at an instant. Find
(a) the points moving upwards
(b) the points moving downwards
(c ) the points which have zero velocity
(d) the points which have maximum velocity
View SolutionA transverse wave is travelling along a string in the positive x-axis. The

shows the photograph of the wave at an instant. Find
(a) the points moving upwards
(b) the points moving downwards
(c ) the points which have zero velocity
(d) the points which have maximum velocity
View Solution
