A head maze is a maze formed by tall rows of hedge. After entering, you search for the center point and then for the exit. Shows the entrance to such a maze and the first two choice we make at the junctions we encounter in moving from point I to point c. We undergo three displacements as indicated in the overhead view of
d1=6.00mθ1=40∘
d2=8.00mθ2=30∘
d3=5.00mθ3=0∘.
where the last segment is parallel to the superimposed x axis. When we reach point c, what are the magnitude and angle of our net displacement →d≠t from point i?
Text Solution
To evaluate we find the x and y components of each disp[lacement .As an example, the components for the first displacement are shown We draw similar diagrams for the outer two displacements and then we apply the x part of to each displacement, using angle relative to the positive direction of the x axis
d1x=(6.00m)cos40∘=4.60m
d2x=(8.00m)cos(−60∘)=4.00m
d3x=(5.00m)cos0∘=5.00m.
Equation then gives us
dnetx=+4.60m+4.00m+5.00m
13.60m.
Similarly, to evaluate we apply the y part of each displacement:
d1y=(6.00m)sin40∘=3.86m
d2y=(8.00m)sin(−60∘)=−693m
d3y=(5.00m)sin0∘=0m.
Equation then gives us
d≠ty=+3.86m−6.93m+0m
=−3.07m.
Next we use these components of →d≠t to construct the vector as shown in the components are in a head-to-tail arrangement and form the legs of a right triangle, the vector forms the hypotenuse, We find the magnitude and angle of →d≠t with The magnitude is
dnet=√d2netx+d2nety
=√(13.60m)2+(3.07m)2=13.9m.
To find the angle ( measured from the positive direction of x), we take an inverse tangent:
θ=tan−1(dnetydnet.y)
=tan−1(−3.07m13.60)=−12.7∘.
The angle is negative because it is measured clockwise from positive x. We must always be alert when we take an inverse tangent on a calculator. The answer it displays is mathematically correct but it may not be the correct answer for the physical situation. In those cases, we have to add 180∘ to the displayed answer, to reverse the vector. To check, we always need to draw the vector and its components as we did in Fig. 3-16d. In our physical situation, the figure shows us that θ=−12.7∘ is a reasonable answer, whereas -12.7∘+180∘=167∘ is clearly not.
We can see all this on the graph of tangent versus angle in Fig. 3-12c. In our maze problem, the argument of the inverse tangent is -3.07/13.60, or -0.226. On the graph draw a horizontal line through that value on the vertical axis. The line cuts through the darker plotted branch at -12.7o and also through the lighter branch at 167∘
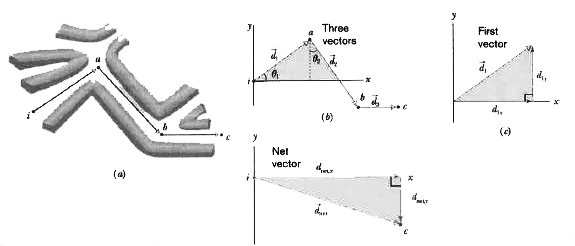
Figure (a) Three displacemnts through a hedge maze. (b) The displacement vectors. (c) The first displacemet vector and its components (d) The net displacement vectorand its components .
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - CHECKPOINT5videos
VECTORS
- BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PROBLEMS34videos
VECTORS
- BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)11videos
UNITS AND MEASUREMENT
- BOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)5videos
WAVE - II
Similar Questions
Knowledge Check
- Question 1 - Select One
At break even point, we have
AR(x)C(x)=1BR(x)=2C(x)CC(x)<R(x)Dp(x)<0 - Question 2 - Select One
A rat will learn to run in a maze even if it is not reinforced for the response:this happens in
AInsight learningBTrial and error learningCUnprepared behaviourDContrapared behaviour - Question 3 - Select One
As we go from periphery to the center of a dicot root , the correct order of tissues that we will encounter is
AEpiblema - Cortex - Endodermis - Metaxylem - Protoxylem - PithBCortex - Epiblema - Endodermis - Metaxylem - Protoxylem - PithCCortex - Epiblema - Endodermis - Protoxylem - Metaxylem - PithDEpiblema - Cortex - Endodermis - Protoxylem - Metaxylem - Pith
How we ____ to ageing is a choice we must make wisely.
View SolutionHow many line segments will we get after joining the points A, B, C and D?
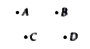 View Solution
View SolutionKartar goes to a movie. The cinema hall has two entrances and three exits. In how many ways can Kartar enter and exit from the hall ?
View SolutionAs we move along an indifferences curve, each point to the right shows
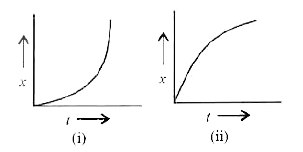
View SolutionFigure (i) and (i) show the displacement-time graphs of two particles moving along the x-axis. We can say that
 View Solution
View Solution

