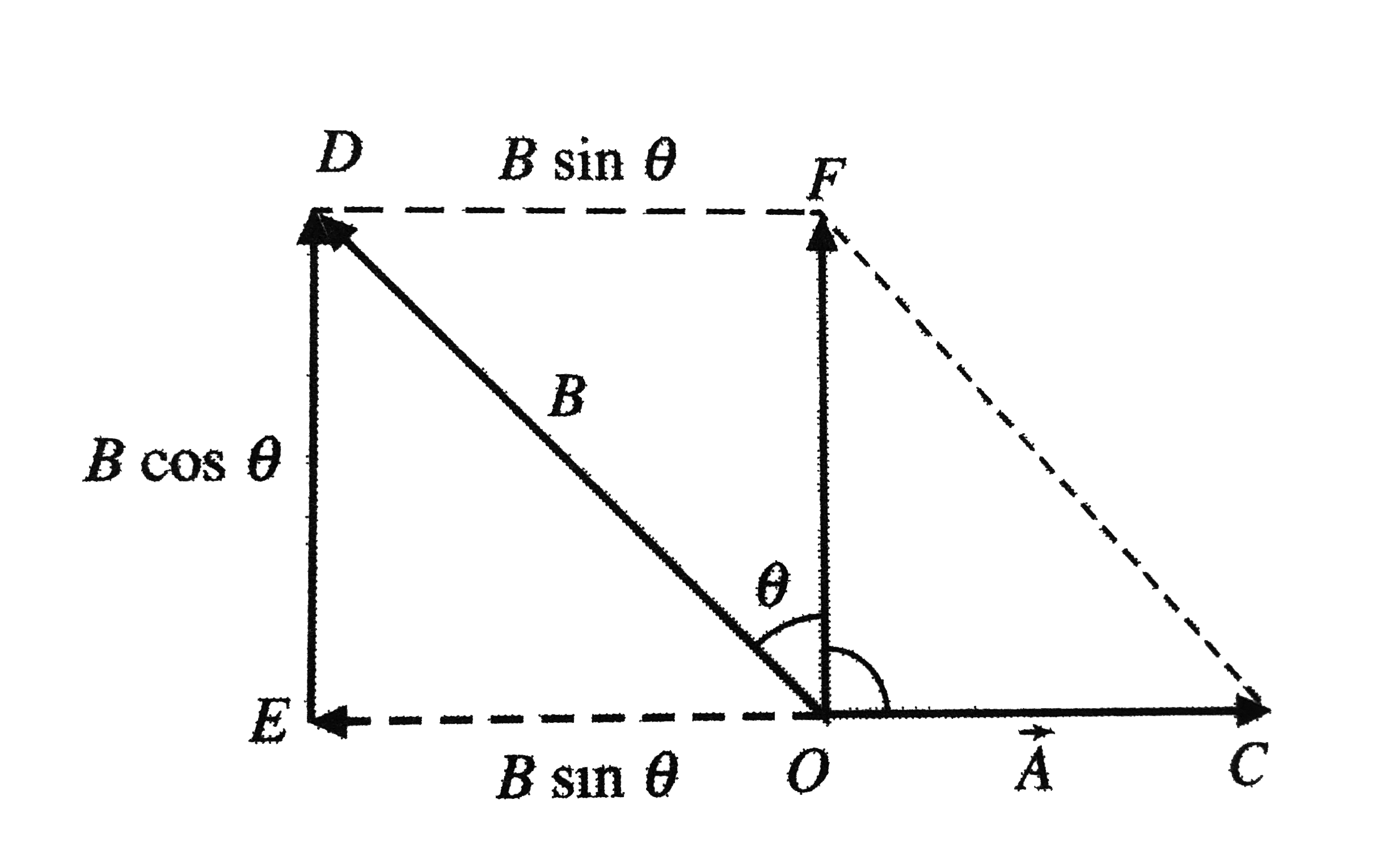
If the x component of a vector →a, in the xy plane, is half as large as the magnitude of the vector, find the tangent of the angle between the vector and the x axis.
To solve the problem, we need to find the tangent of the angle between the vector →A and the x-axis, given that the x-component of the vector is half of its magnitude. Let's break this down step by step.
Step 1: Define the components of the vector
Let the magnitude of the vector →A be |→A|. The x-component of the vector →A can be denoted as Ax. According to the problem, we have:
Ax=12|→A|
Step 2: Use the relationship between components and angle
The x-component and y-component of the vector can be expressed in terms of the angle θ that the vector makes with the x-axis:
Ax=|→A|cos(θ)
Ay=|→A|sin(θ)
Step 3: Substitute the expression for Ax
From the first step, we substitute Ax into the equation:
12|→A|=|→A|cos(θ)
Step 4: Simplify the equation
We can divide both sides of the equation by |→A| (assuming |→A|≠0):
12=cos(θ)
Step 5: Find the angle θ
To find θ, we take the inverse cosine:
θ=cos−1(12)
This gives us:
θ=60∘orθ=300∘(in the fourth quadrant)
Step 6: Calculate the tangent of the angle
The tangent of the angle θ can be calculated using the sine and cosine values:
tan(θ)=sin(θ)cos(θ)
For θ=60∘:
tan(60∘)=√3
For θ=300∘:
tan(300∘)=tan(−60∘)=−√3
Final Result
Thus, the tangent of the angle between the vector →A and the x-axis can be expressed as:
tan(θ)=±√3
Let the magnitude of the vector →A be |→A|. The x-component of the vector →A can be denoted as Ax. According to the problem, we have:
The x-component and y-component of the vector can be expressed in terms of the angle θ that the vector makes with the x-axis:
Ay=|→A|sin(θ)
From the first step, we substitute Ax into the equation:
We can divide both sides of the equation by |→A| (assuming |→A|≠0):
To find θ, we take the inverse cosine:
The tangent of the angle θ can be calculated using the sine and cosine values:
Thus, the tangent of the angle between the vector →A and the x-axis can be expressed as:
Topper's Solved these Questions
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS
39 Videos
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - CHECKPOINT
5 Videos
- UNITS AND MEASUREMENT BOOK - RESNICK AND HALLIDAYCHAPTER - UNITS AND MEASUREMENT EXERCISE - PRACTICE QUESTIONS (MATRIX-MATCH)
11 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
5 Videos
Similar Questions
Knowledge Check
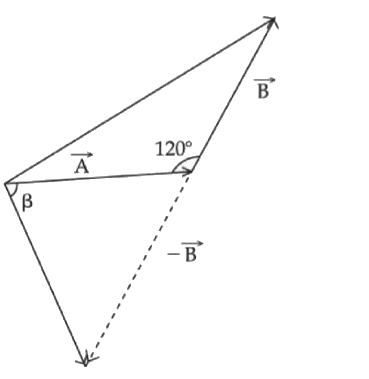
The resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .A120B90C60D150
.A120B90C60D150The x- component of the resultant of several vectors
(i) is equal to the sum of the x-components of the vectors
(ii) may be smaller than the sum of the magnitudes of the vectors
(iii) may be greater than the sum of the magnitudes of the vectors
(iv) may be equal to the sum of the magnitudes of the vectorsA(i),(ii)B(i),(ii),(iv)C(ii),(iii),(iv)DallThe component of a vector →A along y-axis will have maximum value if
A→A makes an angle of 30° with y-axisB→A makes an angle of 60° with y-axisC→A makes an angle of 0° with y-axisD→A makes an angle of 90° with y-axis
The resultant of two vectors →Aand→B perpendicular to the vector →Aanditsmagnitudequal→halfofthemagnitudeofthe→−−→r vec B.F∈doutthe∠between vec A and vec B.
View SolutionTwo vectors, both equal in magnitude, have their resultant equal in magnitude of the either. Find the angle between the two vectors.
View SolutionTwo vectors, both equal in magnitude, hav. e their resultant!! !equal in magnitude of the either vector. Find the angle between the vectors.
View SolutionIf the magnitudes of two vectors are 2and3 and the magnitude of their scalar product is 3√2, then find the angle between the vectors.
View SolutionIf the magnitude of sum of two vectors is equal to the magnitude of difference of the two vectors, the angle between these vectors is
View Solution