A heat engine operates according to a cycle that consists of two isochors and two isobars. Prove that the entropy of the heater-gas-cooler system increases as the engine operates. How does the entropy of the gas change in the process? The heat capacities of the heater and cooler are assumed to he i nfinite
Step by step video & image solution for A heat engine operates according to a cycle that consists of two isochors and two isobars. Prove that the entropy of the heater-gas-cooler system increases as the engine operates. How does the entropy of the gas change in the process? The heat capacities of the heater and cooler are assumed to he i nfinite by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
An ideal gas whose adiabatic exponent equals γ goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises n times both in a isochoric heating and in the isobaric expansion.
View SolutionA sample of oxygen is heated in a process for which the molar specific heat capacity is 2R. During the process the temperature becomes (32)1/3 times of the original temperature. How does the volume of the gas change?
View Solution
Knowledge Check
4 moles of an ideal monoatomic gas is heated isobarically so that its absolute temperature increases 2 times. Then the entropy increment of the gas in this process is
A285.J/kB42.5J/kC57.5J/kD76.5J/kHelium gas goes through a cycle ABCDA (consisting of two isochoric and isobaric lines) as shown in figure Efficiency of this cycle is nearly: (Assume the gas to be close to ideal gas)
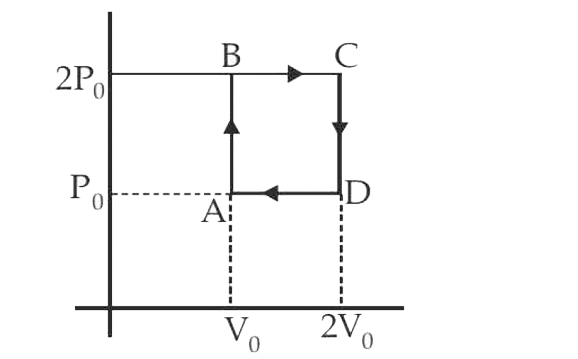A15.4%B9.1%C10.5%D12.5%Two heat engines are operating in such a way that the heat rejected by the first engine is used as the heat input of the second. If both the engines are 40% efficient, then the overall efficiency of the system is
A0.64B0.8C0.5D0.9
Two moles of an ideal gas are cooled isochorically and then expanded isobarically to lower the gas temperature back to the initial value. Find the entropy increment of the gas if in this process the gas pressure changed n=3.3 times.
View SolutionTemperature of two moles of a monoatomic gas is increased by 300K in the process p∝V. Find
(a) molar heat capacity of the gas in the given process
(b) heat required in the given process.
View SolutionMethod 1 of Q
Temperature of two moles of a monoatomic gas is increased by 300 K in the process p∝V.
(a) Find molar heat capacity of the gas in the given process.
(b) Find heat given to the gas in that.
View SolutionA heat engine is a system that converts heat into mechanical work. A heat "source" generates thermal energy that brings a working substance to a high temperature. The working substance then generates work in the engine while transferring heat to a sink at a lower temperature . The working of a heat engine is shownn figure 1.
Heat engines can be modelled using themodynamic cycles. The heat engine given in Figure -2 is of a working substance which is 1.00 mol of a monoatomic ideal gas . The thermodynamic cycle begins at the point designated as '1' and goes clockwise and the values of P and l or V at each point is as given below Fig-2 (P1=1.00atmandV1=24.6L,P2=2.00atm,V3=49.2L,P4=1.00atm)
(a) What is the entropy change of the system for the complete cycle?
(b) If the cycle is reversible , what is the temperature T3?
View SolutionA monatomic gas undergoes a cycle consisting of two isothermals and two isobarics. The minimum and maximum temperatures of gas during the cycle are T1=400K and T2=800K, respectively, and the ratio of maximum to minimum volume is 4.
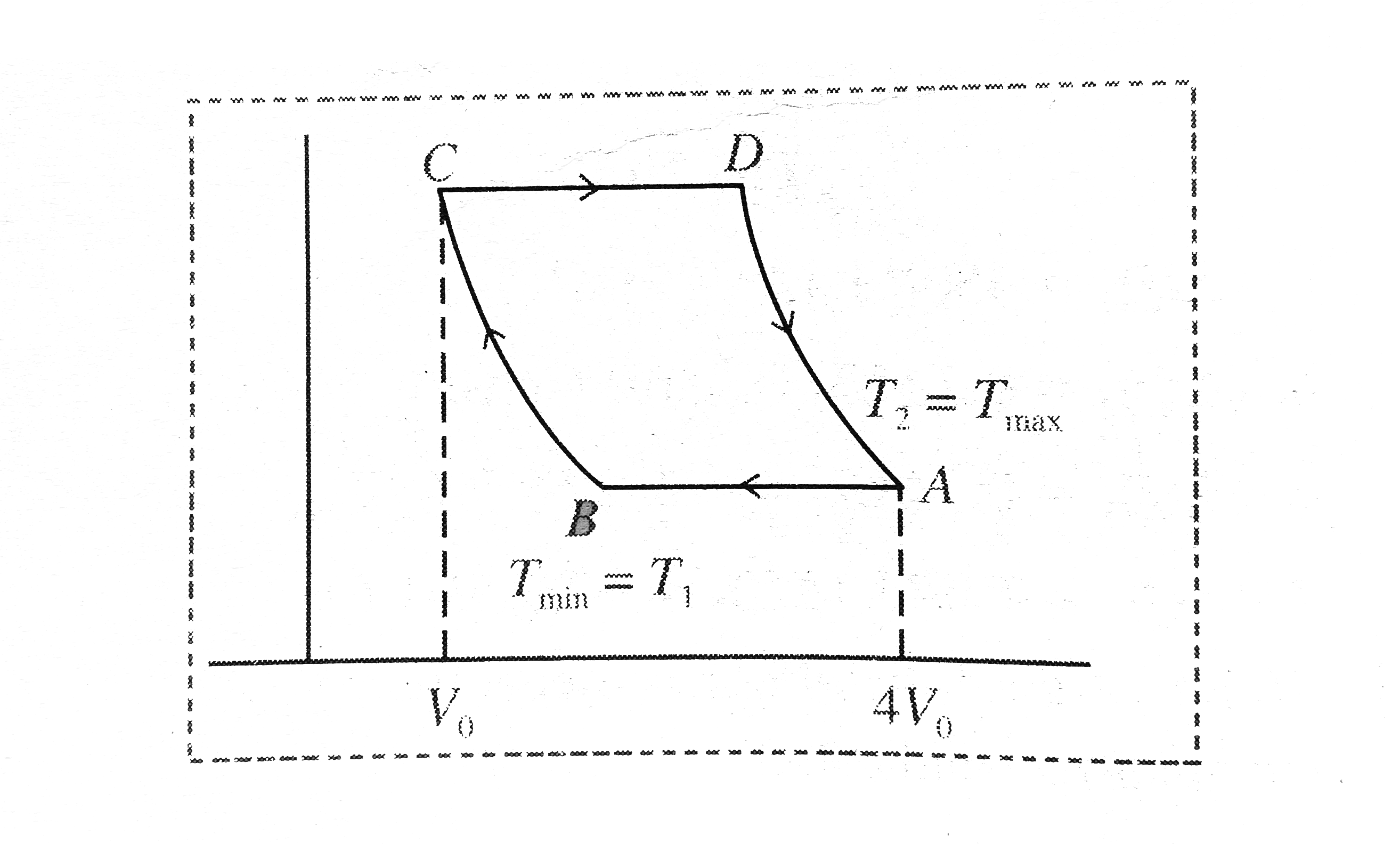
The heat is extracted from the system in process
View Solution