A heavy but uniform rope of lenth L is suspended from a ceiling. (a) Write the velocity of a transverse wave travelling on the string as a function of the distance from the lower end. (b) If the rope is given a sudden sideways jerk at the bottom, how long will it take for the pulse to reach teh celling ? (c ) A particle is dropped from the ceiling at the instant the bottom end is given the jerk where will the particle meet the pulse ?
√4L/g
Topper's Solved these Questions
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - PROBLEMS (LEVEL - I)
59 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
Similar Questions
A transverse wave is travelling on a string. The equation of the wave
View SolutionA heavy but unifrom rope of length L is suspended from a celling . A particle is dropped from the celling at the instant when the bottom end is given a transverse wave pulse. Where will the particle meet the pulse.
View SolutionA uniform rope of mass m and length L hangs from a celling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by t=2√L/g.
View SolutionA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x-along the rope is proportional to
View SolutionA uniform rope of mass 0.1kg and length 2.45m hangs from a ceiling.
(a) Find the speed of transverse wave in the rope at a point 0.5m distant from the lower end.
(b) Calculate the time taken by a transverse wave to travel the full length of the rope.

View SolutionA string of length L and mass M hangs freely from a fixed point . Calculate the velocity of the transverse wave along the string at any position.
(b)Calculate time taken by a transverse pulse to traverse the string.
View SolutionA heavy rope is suspended from the ceiling of a room. If ϕ is the density of the rope, L be its original length and Y be its. Young's modulus, then increase ΔL in the length of the rope due to its own weight is
View SolutionA thick uniform rope of length L is hanging from a rigid support. A transverse wave of wavelength λ0 is set up in the middle of the rope. The wavelength of the wave as it reaches the top most point is
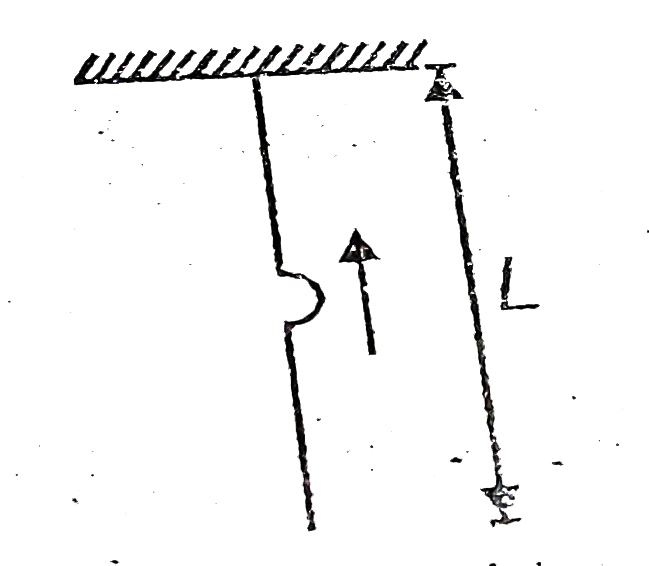
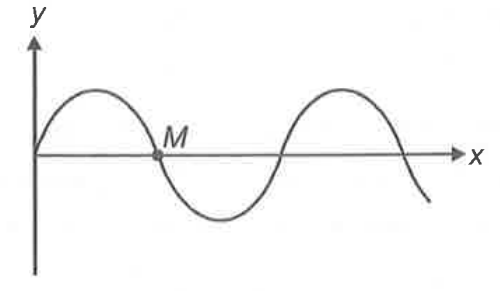
View SolutionA transverse wave is travelling along a string from right to left. The figure represents the shape of the string at the given instant. A point M has a velocity
View SolutionA uniform rope of mass M length L hangs vertically from the ceiling, with lower end free. A distbance on the rope trvelling upwards starting from the lower end has a velocity v. At a point P at distance x from the lower end.
View Solution
