A uniform rope of mass M length L hangs vertically from the ceiling, with lower end free. A distbance on the rope trvelling upwards starting from the lower end has a velocity v. At a point P at distance x from the lower end.
Tension at point P is mg
v=√xg
v=√2xg
Tenstion at point P is (ML)xg
The correct Answer is:B, D
To solve the problem step by step, we will analyze the situation of the hanging rope and the disturbance traveling upwards.
Step 1: Determine the mass per unit length of the rope
The mass of the rope is given as M and its length is L. The mass per unit length μ can be calculated as:
μ=ML
Hint: Remember that mass per unit length is the total mass divided by the total length.
Step 2: Calculate the mass of the rope segment of length x
For a segment of the rope that is x meters long, the mass mx of this segment can be expressed as:
mx=μ⋅x=ML⋅x
Hint: Use the mass per unit length to find the mass of any segment of the rope.
Step 3: Determine the tension at point P
The tension T at point P (which is at a distance x from the lower end) is due to the weight of the rope segment below point P. The weight of this segment is given by:
T=mx⋅g=(ML⋅x)⋅g=M⋅g⋅xL
Hint: The tension in the rope is equal to the weight of the rope segment below the point of interest.
Step 4: Relate the wave velocity to tension and mass per unit length
The velocity v of the wave traveling through the rope can be expressed using the formula:
v=√Tμ
Substituting the expression for tension T from step 3:
v=
⎷M⋅g⋅xLML
Hint: The wave speed depends on the tension and mass per unit length; make sure to simplify correctly.
Step 5: Simplify the expression for wave velocity
Simplifying the equation from step 4:
v=√M⋅g⋅xM=√g⋅x
Hint: Cancel out common terms carefully to arrive at a simpler expression.
Final Results
1. The tension at point P is:
T=M⋅g⋅xL
2. The velocity of the wave at point P is:
v=√g⋅x
The mass of the rope is given as M and its length is L. The mass per unit length μ can be calculated as:
μ=ML
For a segment of the rope that is x meters long, the mass mx of this segment can be expressed as:
mx=μ⋅x=ML⋅x
The tension T at point P (which is at a distance x from the lower end) is due to the weight of the rope segment below point P. The weight of this segment is given by:
T=mx⋅g=(ML⋅x)⋅g=M⋅g⋅xL
The velocity v of the wave traveling through the rope can be expressed using the formula:
v=√Tμ
Substituting the expression for tension T from step 3:
v=
⎷M⋅g⋅xLML
Simplifying the equation from step 4:
v=√M⋅g⋅xM=√g⋅x
1. The tension at point P is:
T=M⋅g⋅xL
2. The velocity of the wave at point P is:
v=√g⋅x
Topper's Solved these Questions
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:LECTURE SHEET (EXERCISE-II (LEVEL-II(ADVANCED) INTEGER TYPE QUESTIONS))
Explore 3 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:LECTURE SHEET (EXERCISE-III (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS))
Explore 10 Videos
- WAVE MOTIONBook:AAKASH SERIESChapter:WAVE MOTIONExercise:LECTURE SHEET (EXERCISE-II (LEVEL-II(ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS))
Explore 6 Videos
- UNITS AND MEASUREMENTSBook:AAKASH SERIESChapter:UNITS AND MEASUREMENTSExercise:EXERCISE -3
Explore 66 Videos
- WAVE MOTION AND SOUNDBook:AAKASH SERIESChapter:WAVE MOTION AND SOUNDExercise:PROBLEMS (LEVEL - II)
Explore 97 Videos
Similar Questions
A uniform rope having linear density λ hangs vertically from the ceiling and its lower end is free. A disturbance produced at the free end has a speed v0 at point P midway on the rope . Then the time taken by the disturbance pulse to reach the ceiling is
View SolutionA uniform rope of mass m and length L hangs from a celling. (a) Show that the speed of a transverse wave on the rope is a function of y, the distance from the lower end, and is given by t=2√L/g.
View SolutionA uniform rope of mass 0.1kg and length 2.45m hangs from a ceiling.
(a) Find the speed of transverse wave in the rope at a point 0.5m distant from the lower end.
(b) Calculate the time taken by a transverse wave to travel the full length of the rope.

View SolutionA uniform rope of mass m hangs freely from a ceiling. A bird of mass M climbs up the rope with an acceleration a. The force exerted by the rope on the ceiling is
View SolutionA Uniform rope having mass m hags vertically from a rigid support. A transverse wave pulse is produced at the lower end. The speed v of wave pulse varies with height h from the lower end as
View SolutionA uniform rope of mass m per unit length, hangs vertically from a support so that the lower end just touches the table top shown in figure. If it is released, show that at the time a length y of the rope has fallen, the force on the table is equivalent to the weight of the length 3y of the rope.

View SolutionA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x-along the rope is proportional to
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
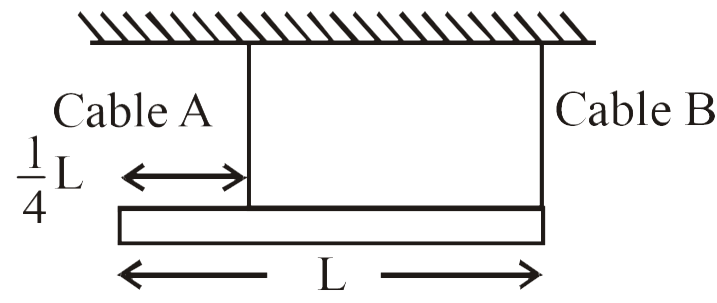
View SolutionA uniform bar of mass M and length L is horizontally suspended from the ceiling by two vertical light cables as shown. Cable A is connected 14th distance from the left end of the bar. Cable B is attached at the far right end of the bar. What is the tension in cable A?
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2

View Solution