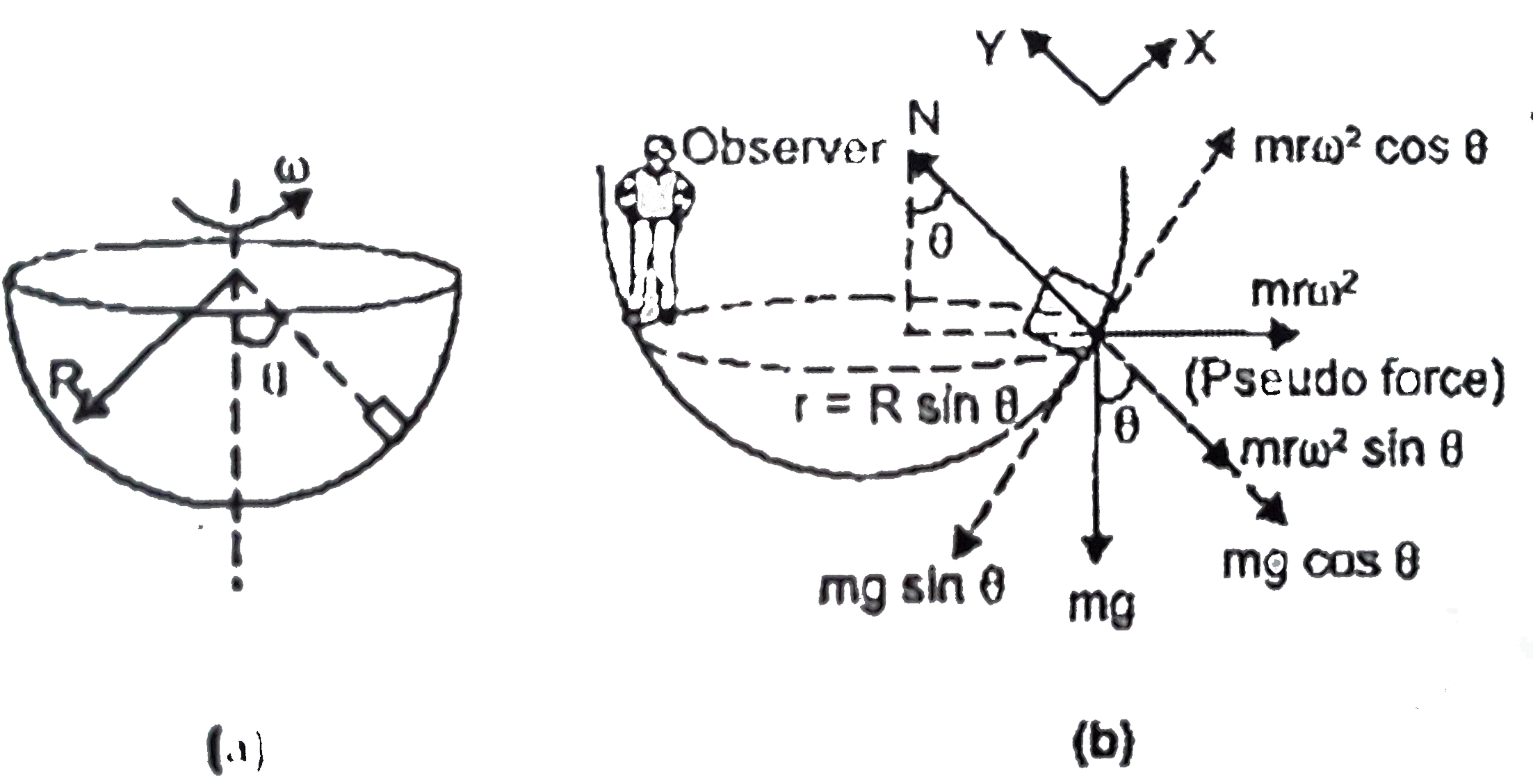
A hemispherical bowl of radius R si set rotating abouv its axis of symmetry whichis kept vertical. A small blcok kept in the bowl rotates with the bowl without slippingn on its surface. If the surfaces of the bowl is mooth, and the abgel made by the radius through the block with the vertical is $θ$ , find the angular speed at which the bowl is rotating.

A

$ω = \sqrt{r g sin θ}$

B

$ω = \sqrt{g / r cos θ}$

C

$ω = \sqrt{\frac{g r}{cos θ}}$

D

$ω = \sqrt{\frac{g r}{tan θ}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let at an instant, the block kept in the bowl be at location $P$ when bowl is rotating with angular velocity $ω$ and block does not ship no bowl, Fig. Let $R$ be the normal reaction of bowl on block. If is acting along $P O$ . Ig $m$ is the mass of the lcok, then in equilibrium position, the horizontal component of $R$ will provide centripetal force and vertical component of $R$ will balance weight of the block. Thus
$R sin θ = m ω^{2} (r sin θ) or R = m ω^{2} r$ ..(i)
and $R cos θ = m g or m ω^{2} r (cos θ) = m g$
[from (i)]
or $ω = \sqrt{\frac{g}{r cos θ}}$

|

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Similar Questions

Knowledge Check

Question 1 - Select One
A hollow cylinder of radius $R$ rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is $f$ hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
A $\frac{g}{2 π^{2} f^{2} R}$
B $\frac{g}{4 π^{2} f^{2} R}$
C $\frac{g}{π^{2} R}$
D $\frac{2 g}{π^{2} f^{2} R}$
Question 2 - Select One
A spherical bowl of radius R rotates about the verical diameter with angular velocity $ω$ .The bowl contains a small object inside and in absence of friction, this object takes up a position inside the bowl such that its radius vector makes an angle $θ$ with the vertical (see figure). Then

A $ω = \sqrt{g / r cos θ}$
B $ω = 2 π g / r$
C $ω = \sqrt{\frac{g cos θ}{r}}$
D $ω = \sqrt{r cos θ \times g}$
Question 3 - Select One
A small coin is kept at the rim of a horizontal circular disc which is set into rotation about vertical axis passing through its centre . If radius of the disc is 10 cm and $μ_{s} = \frac{3}{7}$ , then the angular speed at which the coin will just slip off at
A $5 r a d s^{- 1}$
B $6.54 r a d s^{- 1}$
C $10 r a d s^{- 1}$
D $4.9 r a d s^{- 1}$

Recommended Questions

Home
Ask Doubt
Profile