A hemisphericla bowl of rdius R is rotated about its axis of symetry which is kept vertical.A small block is kept in the bowl at a position where the radius makes an angle θ with the vertical. The block rottes with the bowl without any sliping. The friction coefficient between the block and teh bowl surface is μ. Find the range of the angular speed for which the block will not slip.
The correct Answer is:A, B, C
If et bowl rotates at maximum angular speed, the block tends to slip upwards.
So the frictioN/Al force acts downward.
Here, r=Rsinθ
From the free body diagram 1
R1−mgcosθ−mω2_1(Rsinθ)sinθ
=0……….i
[because r=Rsinθ] and
μR1+mgsinθ−mω2_1(Rsinθ)cosθ
=0 ii.

Substituting the value of R1 from equation i. inequation ii it can be found out that
ω1=(g(sinθ)+μcosθ)Rsinθ(cosθ−μsinθ)]12
again, for minimum speed, the frictioN/Asl force μR2 acrts upwasrd,. From free body diagram -2, it can be prove that
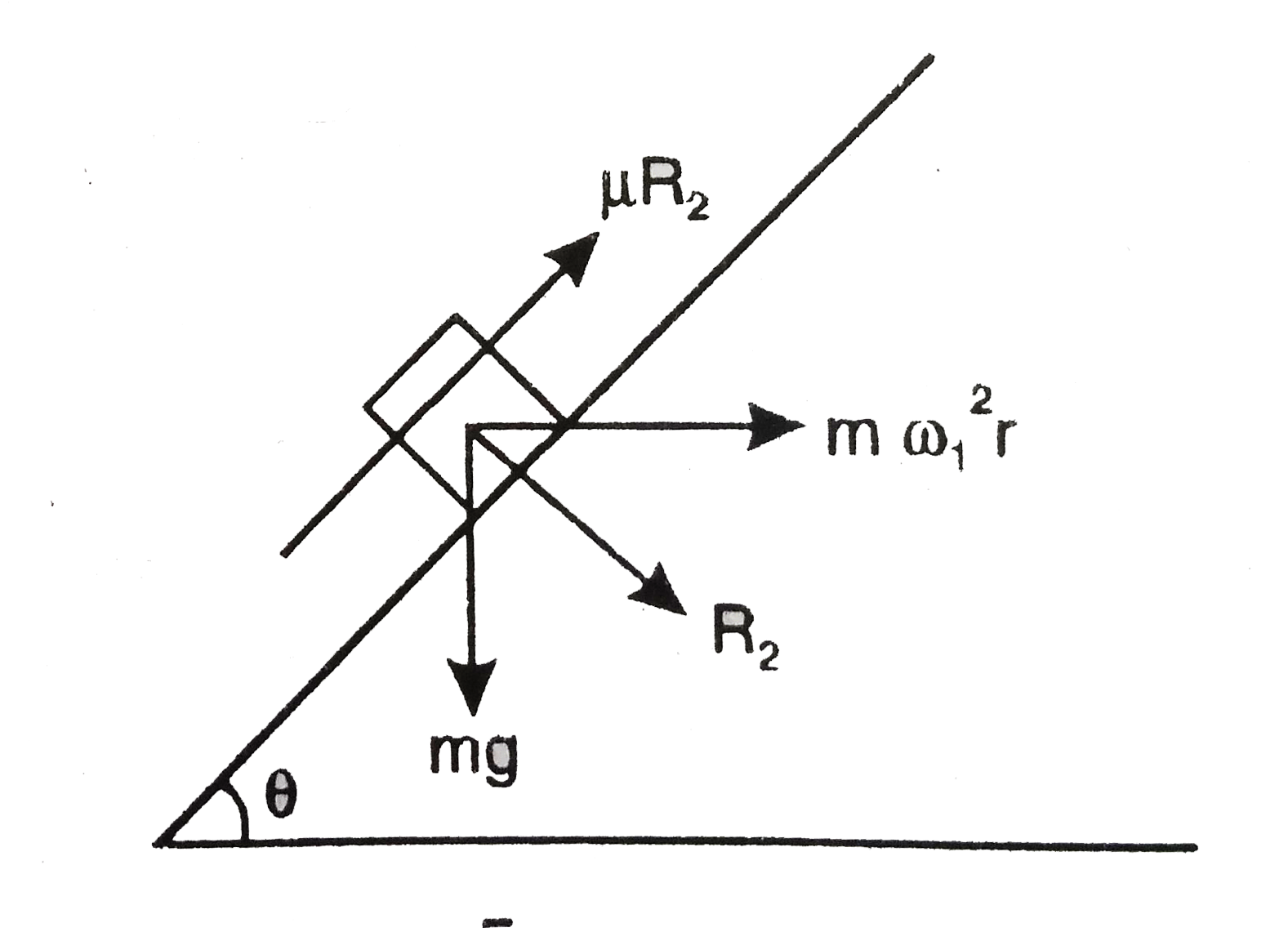
ω2=[g(sinθ+μcosθ)Rsinθ(costhet−μsinθ)]12
∴ the range of speed is betwen ω2andω1
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - HC VERMACHAPTER - CIRCULAR MOTIONEXERCISE - Objective 2
7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMACHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Exercises
64 Videos
- FLUID MECHANICSBOOK - HC VERMACHAPTER - FLUID MECHANICSEXERCISE - Exercises
35 Videos
Similar Questions
A hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View SolutionA hemispherical bowl of radius R is set rotating about its axis of symmetry which is kept vertical. A small block kept in the bowl rotates with the bowl without slipping on its surface. If the surfaces of the bowl is smooth, and the angle made by the radius through the block with the vertical is θ, find the angular speed at which the bowl is rotating.
View Solution
Knowledge Check
A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
AmgcosθB√μ2+1mgcosθCμmgcosθ√μ2+1DμmgθA hollow cylinder of radius R rotates about its axis which is vertical. A block remains in contact with the inner wall if the frequency of rotation is f hertz, but falls at lower frequaencies. The coefficient of friction between the block and the cylinder is
Ag2π2f2RBg4π2f2RCgπ2RD2gπ2f2R
A disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2rads (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without
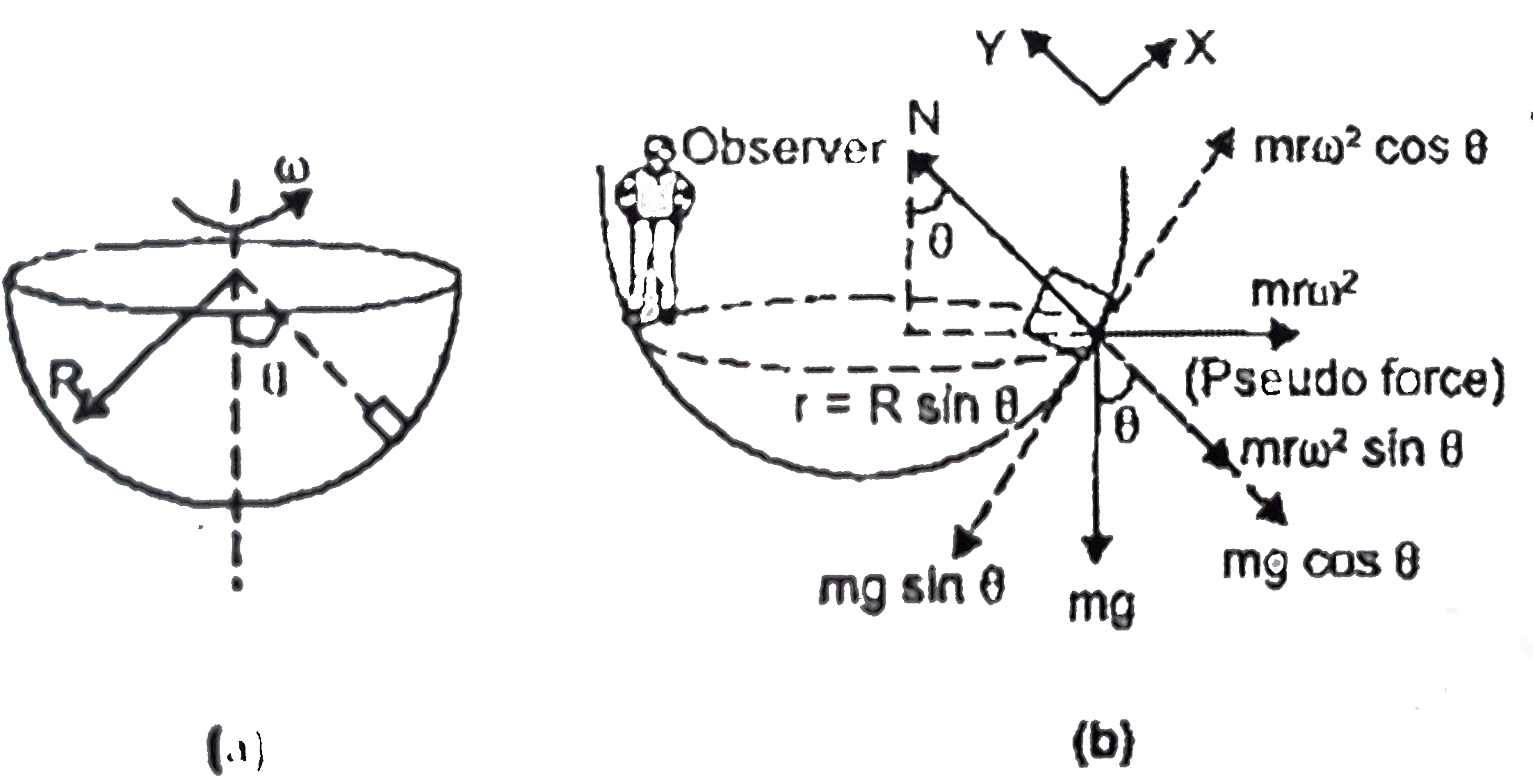
View SolutionA block is kept inside a hemispherical bowl rotating with angular velocity ω. Inner surface of bowl is rough, coefficient of friction is μ. The block is kept at a position where radius makes an angle θ with the vertical. What is the range of the angular speed for which the block will stay at the given position?
View SolutionFind out the distance travelled by the block as shown in figure. If the initial speed of the block is v and μ is the friction coefficient between the surface of block and ground.
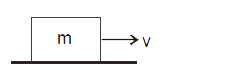
View SolutionFind the acceleration of the block of mass M in the situation of figure. The coefficient of friction between the two blocks is μ1 and that between the bigger block and the ground is μ2.
View SolutionIf the coefficient of friction between an insect and bowl is μ and the radius of the bowl is r, find the maximum height to which the insect can crawl in the bowl.
View Solution
