A hollow sphere of mass M and radius R lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
Mass m moving with velocity v creating rotation in sphere

Conservation of linear momentum
mv=(M+m)vCM⇒vCM=mv(M+m)
Conservation of angular momentum about O
mvh=I0ω=(23MR2+mR2)ω
ω=mvh(23M+m)R2
For pure rolling, vCM=ωR
mvM+m=mvh(23M+m)R
h=(23M+m)R(M+m)=2R3 (Since,m<<M).
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.1
20 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - Check point 9.2
20 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A hollow sphere of mass M lies on a rough horizontal plane when a particle of mass m traveling with speed v collides and sticks with it. If line of motion of the particle is at height h above the center of sphere, find h if the body rolls without slipping after collision (m<<M).
View SolutionThe sphere shown in figue lies on a rough plane when a particle of mass m travbelling at a speed v0 collides and sticks with it. If the line of motion of the particle is at a distance h above the plane, find a. the linear speed o the combine dsystem just after teh collision b. the angular speed of the system about the centre of the sphere just the collistion c. the value of h for which the sphere starts pure rolling on the plane Assume that the mass M of the sphesre is large compared to teh mass of the partcle so that is large compared toteh mass of the particle so that teh centre of mass of the combined system is not appreciably shifted from the centre of the sphere.
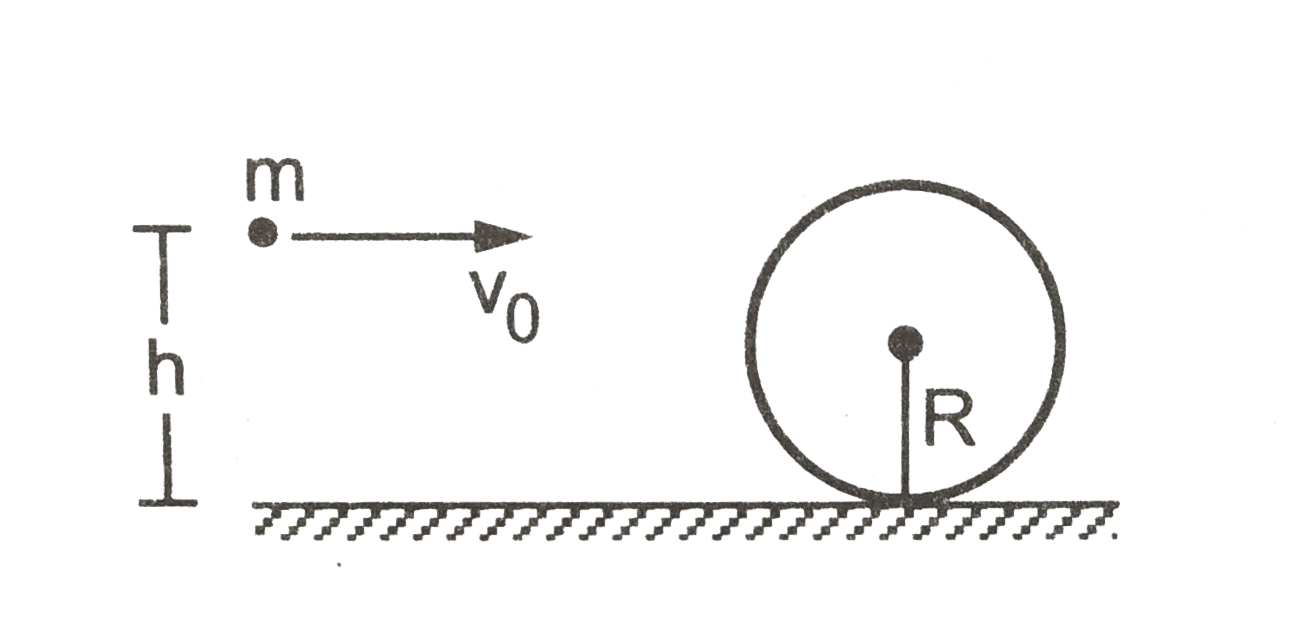
View Solution
Knowledge Check
Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

At what height h above the floor, particle should hit the sphere so that it may start pure rolling after the collision.A5R7B3R5C3R7D7R5Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.
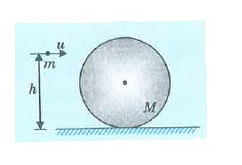
Angular velocity of the sphere just after the collision isA5mu2MRB5mu(h−R)2MR2C2mu(h−R)5MR2D2Mu(h−R)2mR2Sphere of mass M and radius R is kept on a rough horizontal floor. A small particle of mass m, moving horizontally with velocity, collides with the sphere and sticks to it. Line of motion of particle before collision is at a heighth above the floor. Assume that mase of sphere is very large in comparison to particle so that we may assume that centre of mass of the combined system remains at the centre of the sphere after the collision.

What will be the approximate velocity of combined system after the collision?AmuMBmu2MC2muMDzero
A disc of mass m and radius R is kept on a smooth horizontal surface with its plane parallel to the surface. A particle of same mass m travelling with speed v0 collides with the stationery disc and gets embedded into it as shown in the figure. Then

View SolutionA particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with the speed u . Now if it rolls up vertically , the maximum height it would attain will be
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View Solution
